立体几何测试题
班级 姓名 得分 .
一、选择题：
1、直线m与平面
的距离为d，则到m与到平面的距离都为2d的点的集合是………………( )
(A)一个平面 (B)一条直线 (C)两条直线 (D) 空集
2、已知直线l和平面、
、
，给出四个命题：⑴l∥，⊥则l⊥；⑵⊥，⊥则⊥；⑶l
，⊥则l⊥；⑷如果∥，l，则l∥，其中正确的是………………( )
(A)⑷ (B)⑴⑷ (C)⑵⑷ (D)⑶⑷
3、设、表示平面，l表示不在、内的直线，现有三个论断⑴l⊥；⑵⊥；⑶l∥，如果以其中两个作为条件，一个作为结论，则正确命题的个数为…………………………………（ ）
(A)0个 （B）1个 (C）2个 （D）3个
4、在棱长为a的正方体A—C1中，M是AA1的中点，则点A1到平面MBD的距离是………（ ）
(A)
（B）
（C）
（D）
5、在四面体ABCD中，AB=1，AC=2，AD=3，BC=
，BD=
，则AB、CD所成角为……（ ）
(A)30
(B) 45
(C) 60 (D)90
6、在正方体A—C1中，M是AA1的中点，O是底面ABCD的中心，P是棱A1B1上任意一点，则直线OP与直线AM所成角为………………………………………………………………………（ ）
(A)45
(B)60
(C)90 (D)与点P位置有关
7、异面直线a、b成角为，若过空间一个定点P与直线a、b都成75的直线共有3条，则=（ ）
(A) 30 (B) 60 (C) 75
(D)90
8、对于直线m、n和平面、，则⊥的一个充分条件是……………………………………（ ）
(A)m⊥n ，m∥，m∥
(B) m⊥n ，∩=m，n
(C)m∥n，m，n⊥
(D) m∥n，m⊥，n⊥
9、
10、长方体A—C1中，AB=2
，BC=2，AA1=3，以AC为棱，以DAC和D1AC为面的二面角的大小的正切值为………………………………………………………………………………………（ ）
(A)
(B)
(C)1
(D) 
11、空间四边形ABCD中，E、F分别是AB、CD中点，若AD=BC，AD、BC成60，则异面直线EF、BC所成角大小为………………………………………………………………………………（ ）
(A)30
(B) 60
(C)30或60 (D) 90
12、正三棱锥A—BCD中，E在棱AB上，F在棱CD上，并
，设、分别表示EF、AC所成角，EF、BD所成角，则＋=…………………………………………………（ ）
(A)30
(B) 45 (C) 90 (D) 与
的取值有关
二、填空题：
13、正方形ABCD所在平面与正方形ABEF所在平面成60的二面角，则异面直线AD、BF所成角的余弦值为
.
14、P是平面ABC外一点，如果PA=PB=PC，∠APB=∠BPC=∠CPA=60，则二面角P—AB—C的余弦值为
.
15、 .
16、在平面向量中，如果
、
不共线，并且
=(1－t) ＋t,则A、B、P共线，拓展到空间，对空间任意一点O和不共线的三点A、B、C，如果四点共面，则有
.
三、解答题：
17、如图，三棱锥P—ABC的三条棱PC、CA、CB两两互相垂直，并且∠PAC=30，PB=
，BC=3。
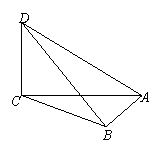⑴求二面角B—PA—C的大小；
⑵设点C在平面PAB上的射影为D，求点D到平面PAC的距离。
18、如图，M、N、P分别是正方体A—C1的棱CC1、B1C1、C1D1的中点。
⑴求证：AP⊥平面D1MN；
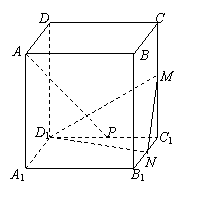⑵求D1C1与平面D1MN所成角的正弦值；
19、正方体A—C1的棱长为a。
⑴求证：平面AB1D1∥平面BC1D；
⑵求平面AB1D1与平面BC1D间的距离。
20、平面、交于直线a，二面角—a—为120，点A∈，点B∈，点A、B到棱a的距离分别为2，4，AB=10。
⑴求AB与棱a所成角的大小；
⑵求直线AB与平面所成角的大小。