立几几何综合练习

姓名

班　级

学 号

时　间

课题

 立体几何综合练习

设　计

一、方法点拨：（1）．初步掌握立体几何中探索性和发散性等命题的解法

（2）提高立体几何综合运用能力，能正确地分析出基本元素及其互相关系，能对图形进行分解组合和变形．

二知能达标：

１．在棱长为ａ的正方体ABCD-A_１B_１C_１D_１中，E.F分别是棱AB与CB的中点，

（１）　 求二面角B-FB_１-E的大小，（２）求点D到平面B_１EF的距离，（３）在

棱DD_１上能否找一点M，使BM⊥平面EFB．如能，试确定点M的位置，如不能，请说明理由．

２．直四棱柱ABCD-A_１B_１C_１D_１的侧棱AA_１的长为ａ，底面ABCD的边长AB＝２ａ，BC=ａ，E为C_１D_１的中点，（１）求证平面BCE⊥平面BDE．（２）求二面角E-BD-C的大小．（３）求三棱锥B_１-BDE的体积．

３．在正三棱锥S-ABC中，高SO＝３，底面边长为，过棱AB作截面ABD交SC于D，设截面与底面所成的二面角为，当何值时，SC⊥平面ABD．

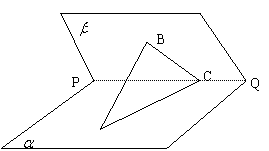４．如图，已知二面角－PQ－为６０⁰，点A和点B分别在平面和平面上，点C在棱PQ上，∠ACP=∠BCP=30⁰,CA=CB=ａ，（１）求证AB⊥PQ；（２）求点B到平面的距离；（３）设R是线段CA上的一点，直线BR与平面所成的角为４５⁰,求线段CR的长度．