高考数学考前模拟训练（二）
一、选择题（本大题共12小题，每小题5分，共60分）
1、在平面直角坐标系中，到x轴的距离是到y轴距离的2倍的点P（x，y）的轨迹方程是A、x-2y=0 B、2x-y=0 C、x-2y=0 D、2x-y=0
2、ΔABC中，A＜B是cosA＞cosB成立的
A、充分但不必要条件 B、必要但不充分条件
C、充分且必要条件 D、既不充分也不必要条件
3、不等式（x-1）
≥0的解集是
A、{xx≥1} B、{xx≥1或x=-2} C、{xx≥-2} D、{xx≥-2且x≠1}
4、已知A+B=
，tanA+tanB=2，则cosAcosB=
A、
B、
C、
D、1
5、已知m，n，m+n成等差数列，又m，n，mn成等比数列，则椭圆
=1的离心率为
A、
B、
C、
D、
6、O是ΔABC所在的平面内的一点，且满足（
—
）·（—
）=0，则ΔABC的形状一定为
A、正三角形 B、等腰直角三角形 C、直角三角形 D、斜三角形
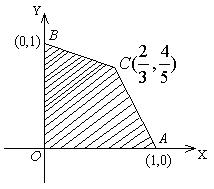7、如图，目标函数
的可行域为四边形OACB (含边界)，若
是该目标函数的最优解，则a的取值范围是 （ ）
A．
B．
C．
D．
8、设O、A、B、C为平面上四个点，
=a，
=b，
=c，且a+b+c=0，a·b=b·c=c·a=－1,则a+b+c等于
A.2
B.2
C.3 D.3
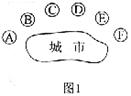
9．某市为改善生态环境，计划对城市外围A、B、C、D、E、F六个区域（如图1）进行治理，第一期工程拟从这六个区域中选取三个，根
据要求至多有两个区域相邻，则不同的选取方案共有
A．6 B．10
C．16 D．15
10、使得Cn1+Cn2+Cn2+…Cnn＜2003不成立的最小的正整数n的值为
A、8 B、9 C、10 D、11
11、函数f（x）=-x3-x，已知x1，x2，x3∈R，且x1+x2≥x3，x2+x3≥x1，x3+x1≥x2，则f（x1+x2+x3）的值
A、大于0 B、小于0 C、不大于0 D、不小于0
12、已知一个半径为
的球中有一个各条棱长都相等的内接正三棱柱，则这一正三棱柱的体积是
A．
B．
C．
D．
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。
13、已知点A（2，0）、B（4，0），动点P在直线y=x上，使得
·
取得最小值的点P的坐标是
；
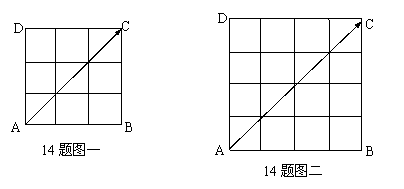
14、如图（一）边长为3的正方形中，有16个交点，从中任取2个组成向量，则与
平行且长度为2的向量个数f(3)=8.
如图（二）边长为4的正方形中，有25个交点，从中任取2个组成的向量与向量平行且长度为3的向量个数f(4)=____________。
 |
15、有一排标号为A、B、C、D、E、F的六个座位，请2名学生和他们的父母共六人入座，要求每对夫妻必须坐在一起，则不同的入座方法总数为 ；（用数字作答）
| A | B | C | D | E | F |
16、设半径为l的圆环在一个正方形(边长大于2)内任意滚动，则该圆环滚不到的平面区的面积(即正方形的四个角区域)为(4－π)．拓展到空间，有：一棱长为3的正方体封闭盒子内有一个半径为1的小球，若将正方体盒子任意翻动，则小球达不到的空间的体积为____________________·
三、解答题：本大题共6小题，共74分。 解答应写出文字说明、证明过程或演算步骤。
17、（本小题满分12分）
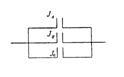在一段线路中并联着3个自动控制的常开开关，只要其中一个开关能够闭合，线路就能正常工作，假定在某段时间内，每个开关能够闭合的概率都是0.7，计算在这段时间内：
（1）开关JA，JB恰有一个闭合的概率；
（2）线路正常工作的概率。
18（本小题12分）已知点A、B、C的坐标分别为A（3，0），B（0，3），
C（cos
，sin）， 
(
)。
（Ⅰ）若∣∣=∣
∣，求角的值；
（Ⅱ）若
=－1，求
的值。
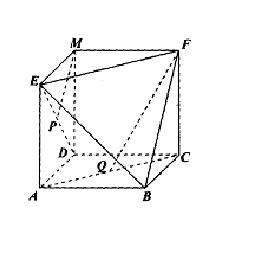19．如图所示，已知四边形ABCD、EADM和MDCF都是边长为a的正方形，点P、Q分别是ED和AC的中点，求：
（1）异面直线PM与FQ所成的角；
（2）四面体P—EFB的体积；
（3）异面直线PM与FQ的距离.
20、（本小题满分14分）
已知f（x）=x3+ax+b定义在区间[-1，1]上，且f（0）=f（1），又P（x1，y1），Q（x2，y2）是其图象上的任意两个点（x1≠x2），
（1）求证：函数f（x）的图象关于点（0，b）成中心对称图形。
（2）设直线PQ的斜率为k，求证：k＜2.
（3）若0≤x1＜x2≤1，求证：y1-y2＜1.
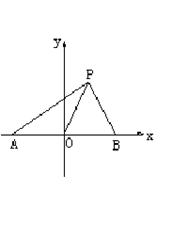
21．如图，在直角坐标系中，点A（-1，0），B（1，0），P（x，y）（
）。设
与x轴正方向的夹角分别为α、β、γ，若
。
（I）求点P的轨迹G的方程；
（II）设过点C（0，-1）的直线
与轨迹G交于不同两点M、N。问在x轴上是否存在一点
，使△MNE为正三角形。若存在求出
值；若不存在说明理由。
高考数学考前模拟训练（二）
一、本大题共12小题，每小题5分，共60分
1、D 2、C 3、B 4、C 5、A 6、C 7、C 8、D 9、A 10、D 11、C 12、B
二、填空题：本大题共4小题，每小题4分，共16分
13、（
，） 14、3π 15、96
16、4个
三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤。
17、（本小题满分12分）本题考查互斥事件有一发生的概率和相互独立事件同时发生的概率，并考查分析问题解决问题的能力
解：分别记在这段时间内开关能够闭合为事件A、B、C，则它们的对立事件为
，
，
且P（A）=P（B）=P（C）=0.7，P（）=P（）=P（）=1-0.7=0.3根据题意在这段时间内3个开关是否能够闭合相互之间没有影响，即事件A、B、C相互独立（2分）
（1）在这段时间内“开关JA，JB恰有一个闭合”包括两种情况：一种是开关JA闭合但开关JB不闭合（事件A·发生），一种是开关JA不闭合但开关JB闭合（事件·B发生），根据题意这两种情况不可能同时发生即事件A·与事件·B互斥。根据互斥事件的概率加法公式和相互独立事件的概率乘法公式，所求的概率是：
P（A·+·B）=P（A+）+P（+B）=P（A）P（）+P（）P（B）
=0.7·0.3+0.3·0.7=0.42（7分）
（2）在这段时间内，线路正常工作，意味着3个开关至少有一个能够闭合，即事件A、B、C至少有一个发生，其对立事件为事件，，同时发生于是所求的概率为：
1-P（··）=1-P（）P（）P（）=1-0.3·0.3·0.3=1-0.027=0.973（11分）
答：开关JA，JB恰有一个闭合的概率为0.42；线路正常工作的概率是0.973（12分）
19、（本小题满分14分）
本题考查函数与绝对值不等式的综合应用，考查综合分析问题和解决问题的能力，充分考查综合应用知识的能力。
证明：（1）∵f（0）=f（1） ∴b=1+a+b ∴a=-1 ∴f（x）=x3-x+b
设（x0，y0）是y=f（x）的图象上的任意一点，则y0=f（x0）=x03-x0+b
∴-y0=-x03+x0-b=（-x03）-（-x0）-b
∴2b-y0=（-x03）-（-x0）+b
故点（- x0，2b-y0）也在y=f（x）的图象上
又点（x0，y0）与点（-x0，2b-y0）关于点（0，b）对称，进而有点（x0，y0）的任意性，得函数f（x）的图象关于点（0，b）成中心对称图形
所以函数f（x）的图象是中心对称图形，且对称中心为点（0，b）（5分）
解法二：（1）∵f（0）=f（1） ∴b=1+a+b ∴a=-1 ∴f（x）=x3-x+b
易知y=x3-x是奇函数，它的图象关于原点对称；而函数f（x）=x3-x+b的图象可由y=x3-x的图象向上平移b个单位得到，故函数f（x）=x3-x+b的图象关于（0，b）对称
所以函数f（x）的图象是中心对称图形，且对称中心为点（0，b）（5分）
（2）∵y1=x13-x1+b，y2=x23-x2+b
∴y1-y2=（x13-x1）-（x23-x2）=（x1-x2）（x12+x22+x1x2-1）
∵x1≠x2
∴k=
=x12+x22+x1x2-1
∵x1，x2∈[-1，1]，x1≠x2
∴3＞x12+x1x2+x22＞0，
-1＜x12+x1x2+x22-1＜2
∴x12+x1x2+x22-1＜2
即k＜2（10分）
（3）∵∴0≤x1＜x2≤1且y1-y2＜2x1-x2=-2（x1-x2）(1)
又 y1-y2=f（x1）- f（x2）= f（x1）- f（0）+ f（1）- f（x2）
≤f（x1）- f（0）+ f（1）- f（x2）≤2x1-0+2x2-1=2（x1-0）+2（1-x2）=2（x1-x2）+2(2)
(1)+(2)得：
2y1-y2＜2，
∴y1-y2＜1（14分）