重点中学
高考数学模拟试题(文理合卷)
第Ⅰ卷（选择题，共60分）
一．选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1． 已知集合P={ 0, m},Q={x│
},若P∩Q≠
,则m等于（ ）
A.1
B.2
C.1或
D. 1或2
2. 在△ABC中，“sin2A>
”
是“A>15
”的（ ）
A.充分不必要条件 B。必要不充分条件
C．充要条件 D。既不充分也不必要条件
3．已知
与L分别是一个平面和一条直线,则内至少有一条直线与直线L( )
A.平行 B.相交 C.异面 D.垂直
4．如图示，向放在水槽底部的烧杯注水（流量一定），
注满烧杯后，继续注水，直至注满水槽，水槽中水面
上升高度h与注水时间t之间的函数关系大致是下列
图像中的（ ）
h h
0 t 0 t
A B
h h
0 t 0 t
C D
5.
[理] 极坐标系中，点（1,
）到圆
上动点的距离的最大值为（ ）
A.
B.
C.2
D.1
[文] 奇函数f(x)在[3,7]上是增函数，在[3,6]上的最大值为8，最小值为-1，则2f(-b)+f(-3)=( )
A.5 B.-5 C.-13 D.-15
6. 已知函数y=sinx-cosx,给出以下四个命题,其中正确的命题是（ ）
A. 若x
[
,
],则y[0,
]
B. 在区间[
]上是增函数
C. 直线
是函数图像的一条对称轴
D. 函数的图像可由函数
的图像向左平移
个单位得到
7．[理] 若直线
、b〉0）始终平分圆
的周长，则
的最小值是（ ）
A. 4
B. 2 C. 
D.
[文] 若直线、b〉0）过圆的圆心，则ab的最大值为（ ）
A.. B.
C.
1
D.2
8. 已知函数y=f(x)是R上的偶函数，且在[0,+∞]上是减函数，若f(m)≤f (3)，则实数m的取值范围是（ ）
A.m≥3 B.m≤-3 或m≥3 C. .m≤-3 D. m≥3
9.在圆
内，过点
有n条弦的长度成等差数列，最短弦长为数列的首项
，最长弦长为
，若公差
，则n的取值集合为 ( )
A.{4,5,6} B.{6,7,8,9} C.{3,4,5} D.{3,4,5,6}
10.[理] 已知A,B,C,D是同一球面上的四点，且连接每两点的线段长都等于2，则球心到平面BCD的距离为( )
A.
B.
C.
D.
[文] 有一棱长为a的正方体框架，其内放置一气球，是其充气且尽可能地膨胀（仍保持为球的形状），则气球表面积的最大值为（ ）
A.
B.2 C.3 D.4
11. 若L是过椭圆一个焦点且与长轴不重合的一条直线，则此椭圆与L垂直且被L平分的弦（ ）
A.有且只有一条 B. 有且只有2条
C.有3条 D. 不存在
12．对某种产品的6件不同正品和4件不同次品一一进行测试，到区分出所有次品为止。若所有次品恰好在第五次测试被全部发现，则这样的测试方法有（ ）
A.24种 B.96种 C.576种 D.720种
第Ⅱ卷 (非选择题,共90分)
二.填空题: 本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
13 .[文] 已知函数f(x)=2
,则使得数列
成等差数列的非零常数p与q所满足的关系式为
.
[理]在下面等号右侧两个分数的分母方块处,各填上一个自然数,并且使这两个自然数的和最小:1=
.
14.一个圆柱形容器的内半径为5cm,两个直径为5的玻璃小球被浸没于容器的水中,当取出这两个小球后, 容器的水面下降了x cm, 则x= .
15.某校有学生宿舍若干间,现安排高三女生居住,若每间住5人,余60人. 若每间住10人,则有一间宿舍不空也不满,则高三女生有 人,宿舍有 间.
16已知双曲线
的左支上存在一点P到左焦点的距离是点P到右焦点距离和到左准线距离的比例中项,则双曲线的离心率e的取值范围是
.
三.解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
17.( 本小题满分12分)
已知复数z=sinB+(1-cosB)i ,argz=
A, B, C是⊿ABC的内角。
（１）求Ｂ； （２）求sinA+sinC的取值范围。 A
18. .( 本小题满分12分)
如图，正三角形ABC与直角三角形BCD成直二面角，
且∠BCD=90,∠CBD=30.
(１) 求证：AB⊥CD;
B
C
（２）求二面角D-AB-C的正切值。 D
（3）[理]求异面直线AC和BD所成的角。
19. .( 本小题满分12分)
经过抛物线y
的焦点F的直线L与该抛物线交于A,B两点.
（1） 若线段AB的斜率为k，试求中点M的轨迹方程；
（2） 若直线的斜率k＞2，且点M到直线3 x+4y+m=0的距离为
，试确定m的取值范围。
20. .( 本小题满分12分)
设数列
前项和为
,且(3
,其中m为常数,m
(1) 求证:是等比数列;
(2) 若数列的公比q=f(m),数列
满足
求证:
为等差数列,求
.
21. .( 本小题满分12分)
随着我国加入WTO，某企业决定从甲、乙两种产品中选择一种进行投资生产，打入国际市场。已知投资生产这两种产品的有关数据如下表（单位：万美元）
|
类 别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多生产的件数 |
| 甲产品 | 30 | a | 10 | 200 |
| 乙产品 | 50 | 8 | 18 | 120 |
项 目 其中年固定成本与生产的件数无关，a为常数，且4≤a≤8。令外，年销售x件乙产品时需上交0.05x
万美元的特别关税。
（１） 写出该厂分别投资生产甲、乙两种产品的年利润y
,y
与生产相应产品的件数x (x
之间的函数关系式；
（２） 分别求出投资生产这两种产品的最大年利润；
（３） 如何决定投资可获最大年利润。
.22. ( 本小题满分14分)
已知
函数f(x)=
的图像关于原点对称，其中m,n为实常数。
（１） 求m , n的值；
（２） 试用单调性的定义证明：f (x) 在区间[-2, 2] 上是单调函数；
（３） [理科做] 当-2≤x≤2 时，不等式
恒成立，求实数a的取值范围。
参 考 答 案
一.DADBB(D)
CABAC(B) DC
二.13.p=q. (文)4,12 14.
.
15.125,13.
16.1<e
.
三.(17)∵argz=
,∴
∴tan
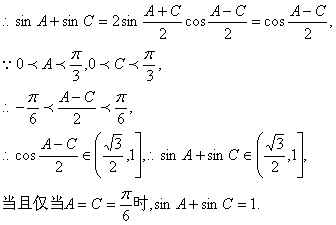
(18) ( 1)∵平面ABC⊥平面BCD, ∠BCD=90,∴CD⊥平面ABC.
∵AB
平面ABC, ∴CD⊥AB.
(2)过点C作CM⊥平面ABC于M,连DM,由(1)知CD⊥平面ABC,
∴DM⊥AB.∴∠CMD是二面角 D-AB-C的平面角.
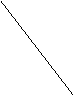设,CD=1,由∠BCD=90,∠CBD=30,BC=
A
∵⊿ABC是正三角形, ∴CM=
M N
∴tan∠CMD=
B
O
C
故二面角D-AB-C的正切值为 
.
D
(3) 取三边AB,AD,BC的中点M .N . O,连AO,NO,MN,OD.则OM平行且等于AC,MN平行且等于BD.
∴直线OM和MN所成的锐角或直角就是直线AC和BD所成的角.
∵⊿ABC是正三角形,且平面ABC⊥平面BCD,
∴AO⊥平面BCD,∴⊿AOD是直角三角形,
ON=
又∵CD⊥平面ABC,
∴AD=
在⊿OMN中,OM=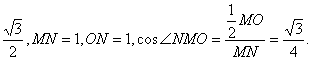
∴直线AC和BD所成角为arccos
.
19.(1)设A(
直线AB的方程为y=k(x-1) (k≠0),代入
,得
kx-(2k+4)x+k=0
设M(x ,y).则
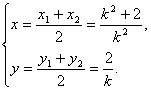
∴点M的坐标为(
消去k可得M的轨迹方程为
(2)由 d=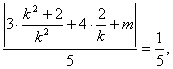
得
即
0＜
＜,得
0＜
,
即 
或 
故的取值范围为 (-
（20）（1）由
∴是等比数列。
（2）
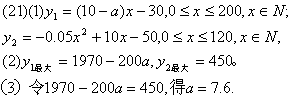
当4
时，投资甲产品；当7.6<a
时，投资乙产品；当a=7.6时，投资甲、乙两产品均可。
(22)(1)由于f(x)图象关于原点对称，则f(x)是奇函数,
f(-x)=-f(x) 
∴f(x)在[-2,2]上是减函数。
（3）由（2）知f(x)在[-2,2]上是减函数，则-2
时,
故-2
不等式f(x)
恒成立
