高考数学模拟试题
一、 选择题：（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一个项是符合题目要求的）
1、设集合
，
，
是从集合
到集合
的映射，则在映射
下，象
的原象有 【 】
A．1个 B．2个 C．3个 D．4个
2、在复平而内，将复数
对应向量顺时针旋转2弧度，所得向量对应复数是
【 】
A．
B．
C．
D．
3、圆锥的侧面展开图是一个半径为12的半圆，则这个圆锥的内切球的体积是 【 】
A．
B．
C．
D．
4、[理] 下列不等式在区间
内恒成立的是
【 】
A．
B．
C．
D．
[文] 下列不等式的在区间
内恒成立的是
【 】
A． B．
C．
D．
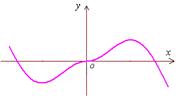
5、函数
的图象如图所示，则
的解析式可能是
【 】
A．
B．
C．
D．
6、磁悬浮列车是一种高科技含量的新型交通工具，它具有速度快，爬坡能力强，能耗低等优点，其每个座位的平均能耗仅是飞机每个座位平均能耗的三分之一，是汽车每个座位平均能耗的70%，那么汽车每个座位的平均能耗是飞机每个座位平均能耗的 【 】
A．
B．
C．
D．
7、已知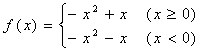
，则不等式
解的区间是【 】
A．
B．
C．
D．
8、[理] 方程
（
∈R且
）表示的曲线是 【 】
A．以点
、
为端点的线段
B．过点、的直线
C．过点、两点的直线，去掉点
的部分
D．过点、两点的直线去掉
的部分
[文] 圆
上的点到直线
的距离的最小值是4，则r的值为【 】
A．3 B．2 C．1 D．±1
9、设a、b是两条不同的直线，
、
是两个不同的平面，则下列四个命题：
①
若
，
，
，则
； ②若
, 
，则
；
③若，，则或
；④若，，
，则
其中正确命题的个数为 【 】
A．0 B．1 C．2 D．3
10、一水池有2个进水口，1 个出水口，进出水速度如图甲、乙所示. 某天0点到6点，该水池的蓄水量如图丙所示.（至少打开一个水口）
 |
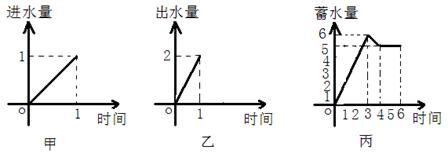给出以下3个论断：
①0点到3点只进水不出水；②3点到4点不进水只出水；③4点到6点不进水不出水.则一定能确定正确的论断是 【 】
A．① B．①② C．①③ D．①②③
11、二次曲线
，当
时，该曲线的离心率
的取值范围是【 】
A．
B．
C．
D．
]
12、正三棱锥
的侧棱长和底面边长相等，如果E、F分别为SC，AB的中点，那么异面直线EF与SA所成角为
【 】
A．
B．
C．
D．
第ll卷
二、填空题（本大题共4小题，共16分，把答案填在题中的横线上）
13．2003年10月15日，我国自行研制的载人宇宙飞船“神州五号”在酒泉卫星发射中心胜利升空，实现了中华民族千年的飞天梦，飞船进入的是距地球表面近地点高度约200公里，远地点约350公里的椭圆轨道（地球半径约为6370公里），则轨道椭圆的标准方程为（精确到0.1公里） .（注：地球球心位于椭圆轨道的一个焦点）
14．某医药研究所研制了5种消炎药X1、X2、X3、X4、X5和4种退烧药T1、T2、T3、T4，现从中取出两种消炎药和一种退烧药同时进行疗效试验， X1、X2两种消炎药必须同时搭配使用，但X3和T4两种药不能同时使用，则不同的试验方案有 种（用数字作答）.
15．长方体的一条对角线与各个面所成的角分别为
，则
_________ .
16．一种专门占据内存的计算机病毒，开机时占据内存2KB，然后每3分钟自身复制一次，复制后所占内存是原来的2倍，那么开机后经过 分钟，该病毒占据64MB内存. (1MB=210KB)
三、解答题（本大题共6小题，共74分，解答应写出文学说明，证明过程或演算步骤）
17．（本小题满分12分）[理] 非等边三角形ABC的外接圆半径为2，最长的边
，求
的取值范围.
[文] 已知
且
,解关于
的不等式
.
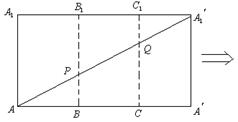
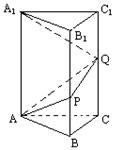18．（本小题满分12分）如图，将长
，宽
的矩形沿长的三等分线处折迭成一个三棱柱，如图所示：
（l）求平面APQ与底面ABC所成二面角的正切值；
（ll）求三棱锥
的体积.
19．（本小题满分12分）数列
的前n项和为
，且
，数列
满足
.（l）求数列
的通项公式；
（ll）[理] 数列
的前n项和为
，求
；[文] 求数列
的前n项和.
20．（本小题满分12分）
已知抛物线
上有两点A、B关于点
对称.
（l）求
的取值范围；
（ll）当
时，AB的垂直平分线交该抛物线于C、D两点，问平面内是否存在一点N到A、B、C、D四点的距离相等，若存在，求出点N的坐标，若不存在，请说明理由.
21．（本小题满分12分）
某地为了防止水土流失，植树造林，绿化荒沙地，每年比上一年多植相同亩数的林木，但由于自然环境和人为因素的影响，每年都有相同亩数的土地沙化，具体情况为下表所示：
| 1998年 | 1999年 | 2000年 | |
| 新植亩数 | 1000 | 1400 | 1800 |
| 沙地亩数 | 25200 | 24000 | 22400 |
而一旦植完，则不会被沙化：
问：（l）每年沙化的亩数为多少？
（ll）到那一年可绿化完全部荒沙地？
22．（本小题满分14分）
设
是定义域在
上的奇函数，且其图象上任意两点连线的斜率均小于零.
（l）求证在上是减函数；
（ll）如果
，
的定义域的交集为空集，求实数
的取值范围；
（lll）证明若
，则，存在公共的定义域，并求这个公共的空义域.
高考模拟考试（一）
数学试题参考答案
一、选择题
1——5、CC DC（C）D 6——10、C AD(D)DA 11——12、CC
二、填空题
（13）
； （14）14； （15）2； （16）45；
三、解答题
17（理）由正弦定理
得
∵BC是最长边，且三角形为非等边三角形
∴
………………………………………………………………………4分
) …………………………………………………………8分
又
∴
………………………………………………………………10分
∴
故 
的取值范围为
………………………………………12分
（文）原不等式等价于
………………………………………………2分
即
………………………………………………4分
∴
…………………………………………………………………8分
∴当
时，原不等式的解集为
；
当
时，原不等式的解集为
.………………………………12分
18、（Ⅰ）依题意知
三棱柱
是正三棱柱，且侧棱
，底面边长为
，BP=1，CQ=2
延长QP交BC延长线于点E，连AE
在△ACE中， 
，
，∠ACE=60°，于是AE=3
过C作CF⊥AE于F，连QF
则∠QFC为平面APQ与平面ABC所成的锐二面角……………………………………4分
于是
即：平面APQ与面ABC所成锐二面角的正切值为
………………………………6分
（Ⅱ）连
，
的面积为
………………………………………………………………8分
点Q到平面
的距离为
∴
…………………………………12分
19、（Ⅰ）当n=1时 
∴
………………………………………2分
当n≥2时 
∴
……………………………………………………………………………4分
于是数列{
}是首项为1，公比为2的等比数列
∴
………………………………………………………………………………6分
（Ⅱ）（理）∵
∴
从而
…，…
上式相加得
，又
∴
……………………………………………………………………8分
………………………………………………………………………10分
………………………………………12分
（文）∵
∴
从而
…，…
上式相加得
，又
∴………………………………………………………………8分
……………………………………………………………………12分
20 、（１）设
是关于点M（2，2）对称的抛物线上两点
则：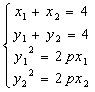
………………………………………………………………………2分
得：
得：
从而
是方程
的两个不等实根…………………………4分
∴
∵
………………………………………………………………………………………6分
（2）抛物线方程为
，且A，B两点在其抛物线上
则：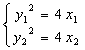 
∴
又
∴
得AB所在直线斜率为
从而CD所在直线斜率为
直线AB方程为
直线CD的方程为
…………………………………………………………8分
由
，解得：
由
消x得：
设
、
∴
从而 
∴CD的中点P的坐标为
，且
……………………………………10分
∴
而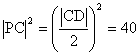 
∴
故存在这样的点N，其坐标为……………………………………………12分
21．（1）由表知，每年比上一年多造林400亩.
因为1999年新植1400亩，故当年沙地应降为
亩，但当年实际沙地面积为24000亩，所以1999年沙化土地为200亩. ………………4分
同理2000年沙化土地为200亩.
所以每年沙化的土地面积为200亩…………………………………………………6分
（2）由(1)知，每年林木的“有效面积”应比实造面积少200亩.
设2000年及其以后各年的造林亩数分别为
、
、
、…，则n年造林面积总和为：
………………………………………………8分
由题意：
化简得
解得： 
…………………………………………………………………10分
故8年，即到2007年可绿化完全部沙地. ………………………………………12分
22 （1）∵奇函数
的图像上任意两点连线的斜率均为负
∴对于任意
且
有
……………………………………………………3分
从而
与
异号
∴在
上是减函数…………………………………………5分
（2） 
的定义域为
的定义域为
………………………………7分
∵ 上述两个定义域的交集为空集
则有： 
或
…………………………9分
解得：
或
故c的取值范围为或………………………………………………10分
（3）∵ 
恒成立
由(2)知：当
时
当
或
时
且 
此时的交集为
………………………………………12分
当
且 
此时的交集为
故时，存在公共定义域，且
当或时，公共定义域为；
当时，公共定义域为.…………………………14分