高考数学试题3
一、 选择题(每小题5分，共60分)
1.已知集合M＝{xx2＜4
，N＝{xx2－2x－3＜0，则集合M∩N＝
A.{xx＜－2 B.{xx＞3} C.{x－1＜x＜2 D.{x2＜x＜3
2.
＝
A.
B.1 C.
D.
3.设复数ω＝－＋
i，则1＋ω＝
A.–ω B.ω2 C.
D.
4.已知圆C与圆(x－1)2＋y2＝1关于直线y＝－x对称，则圆C的方程为
A.(x＋1)2＋y2＝1 B.x2＋y2＝1 C.x2＋(y＋1)2＝1 D.x2＋(y－1)2＝1
5.已知函数y＝tan(2x＋φ)的图象过点(
,0)，则φ可以是
A.－
B. C.－ D.
6.函数y＝－ex的图象
A.与y＝ex的图象关于y轴对称 B.与y＝ex的图象关于坐标原点对称
C.与y＝e－x的图象关于y轴对称 D.与y＝e－x的图象关于坐标原点对称
7.已知球O的半径为1，A、B、C三点都在球面上，且每两点间的球面距离为
，则球心O到平面ABC的距离为
A.
B.
C.
D.
8.在坐标平面内，与点A(1,2)距离为1，且与点B(3,1)距离为2的直线共有
A.1条 B.2条 C.3条 D.4条
9.已知平面上直线L的方向向量e＝(－
,
)，点O(0,0)和A(1,－2)在L上的射影分别是O1和A1，则
＝
e，其中＝
A.
B.－ C.2 D.－2
10.函数y＝xcosx－sinx在下面哪个区间内是增函数
A.(,
) B.(
,2) C.(,
) D.(2,3)
11.函数y＝sin4x＋cos2x的最小正周期为
A.
B. C. D.2
12.在由数字1,2,3,4,5组成的所有没有重复数字的5位数中，大于23145且小于43521的数共有
A.56个 B.57个 C.58个 D.60个
二、 填空题(每小题4分，共16分)
13.从装有3个红球，2个白球的袋中随机取出2个球，设其中有个红球，则随机变量的概率分布为
| ξ | 0 | 1 | 2 |
| P |
14.设x，y满足约束条件：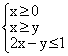
，则z＝3x＋2y的最大值是＿＿＿＿。
15.设中心在原点的椭圆与双曲线2x2－2y2＝1有公共的焦点，且它们的离心率互为倒数，则该椭圆的方程是＿＿＿＿。
16.下面是关于四棱柱的四个命题：
①若有两个侧面垂直于底面，则该四棱柱为直四棱柱；
②若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱；
③若四个侧面两两全等，则该四棱柱为直四棱柱；
④若四棱柱的四条对角线两两相等，则该四棱柱为直四棱柱。
其中，真命题的编号是＿＿＿＿(写出所有真命题的编号)
三、 解答题(本大题共6个小题，共74分)解答应写出文字说明，证明过程或演算步骤
17.(本题满分12分)已知锐角三角形ABC中，sin(A＋B)＝，sin(A－B)＝
。
(1)求证：tanA＝2tanB；
(2)设AB＝3，求AB边上的高。
18.(本题满分12分)已知8支球队有3支弱队，以抽签方式将这8支球队分为A、B两组，每组4支。求：
(1)A、B两组中有一组恰有两支弱队的概率；
(2)A组中至少有两支弱队的概率。
19.(本题满分12分)数列{an}的前n项和记为Sn，已知a1＝1，an＋1＝
Sn(n＝1,2,3,…)。证明：
(1)数列{
}是等比数列；
(2)Sn＋1＝4an。
20.(本题满分12分)如图，直三棱柱ABC—A1B1C1中，∠ACB＝90o，AC＝1，CB＝
，侧棱AA1＝1，侧面AA1B1B的两条对角线交点D，B1C1的中点为M。
(1)求证：CD⊥平面BDM；
(2)求面B1BD与面CBD所成二面角的大小。
21.(本题满分12分) 给定抛物线C：y2＝4x，F是C的焦点，过点F的直线L与C相交于A、B两点。
(1)设L的斜率为1，求
与
夹角的大小；
(2)设
＝
，若∈[4，9]，求L在y轴上截距的变化范围。
22.(本题满分14分)已知函数f(x)＝ln(1＋x)－x，g(x)＝xlnx。
(1)求函数f(x)的最大值；
(2)设0＜a＜b，证明：0＜g(a)＋g(b)－2g(
)＜(b－a)ln2