高三第二学期数学练习卷
一、填空题：（每题4分，共48分）
1．若集合
，则
。
2．已知
，则
。
3．已知向量
，若向量
垂直，则实数
。
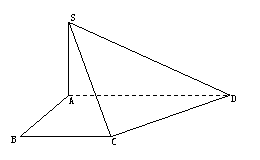4．如图，在直角梯形
中，
∥
,
，又
，垂足
为
，且
，则二面角
的大小
为 。（用反三角函数表示）
5．若复数
，则
。
6．函数
的反函数
。
7．已知向量
，将向量
绕原点按顺时针方向旋转
，且长度伸长到原来的
倍，得到向量
，则
。
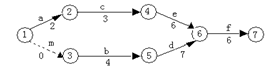
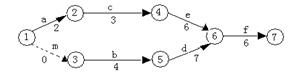
8．（文）某工程的工序流程图如下，则总工
时数为 天。
（理）曲线
（
）与直线
的交点坐标是
。
9．在集合
中任取一个元素，其恰好满足三角方程
的概
率为 。（用分数作答）
10．设直线
与直线
的夹角为
，则
，若直线
与
的夹角为
，则
。
11．对于正数
和
，其中
，定义
，其中
是满足
的最大整数，则
。
12．如图（1）所示，三棱锥S—ABC
被平行于底面的平面所截，得到
三棱锥S—DEF，则两棱锥的体积
之比为
。
如图（2）所示，将上述真命题加以推广，即要求得到更一般的真命题，而已知的命题应成
为所推广命题的一个特例，推广的命题为：
。
二、选择题（每题4分，共16分）
13．已知
，则
在
上的射影为
（ ）
（A） 
； （B） 
； （C） 
； （D） 
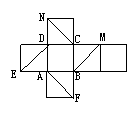
14．右图是正方体的平面展开图，在这个正方体中，
① BM与ED平行；② CN与BE是异面直线；
③ CN与BM成60°；④ DM与BN垂直。
以上四个命题中，正确命题的序号是 （ ）
（A） ①②③ （B） ②④ （C） ③④ （D） ②③④
15．函数
的奇偶性是
（ ）
（A）奇非偶（B）偶非奇（C）既奇又偶 （D)非奇非偶
16．四面体的顶点和各棱中点共10个点，在其中取4个不共面的点，不同的取法共有（ ）
（A） 150种 （B） 147种 （C） 144种 （D） 141种
三、解答题：（12分+12分+16分+16分，共56分）
17．、
、
为
的三个内角，已知
是
中
项的系数，且
，求、、。
解：
18．已知
︱︱
是、
的夹角，
为何值时，
为最大角，并求此时的坐标。
解：
19．如图，在正三棱柱ABC—A1B1C1中，各棱长都相等，D，E分别为AC1，BB1的中点.
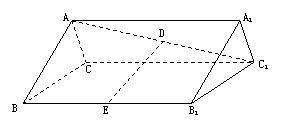（1）求证：DE//平面A1B1C1；
（2）求二面角A1—DE—B1的大小.
20、已知
是定义在
上的恒不为零的函数，且对于任意的
、
都满足：
（1）求
的值，并证明对任意的
，都有
；
（2）设当
时，都有
，证明在
上是减函数；
（3）设
时，
表示数列
的前项和，
（文）求
；
（理）在（2）的条件下，求集合
中的最大元素和
最小元素。
解：
高三第二学期数学练习卷解答
一、填空题：（每题4分，共48分）
1．若集合
，则 
。
2．已知
，则
。
3．已知向量，若向量垂直，则实数 
。
4．如图，在直角梯形中，∥
，
又，垂足为，且，
则二面角的大小为 
。
（用反三角函数表示）
5．若复数，则
。
6．函数的反函数 
。
7．已知向量，将向量绕原点按顺时针方向旋转，且长度伸长到原来
的倍，得到向量，则 
。
8．（文）某工程的工序流程图如下，则总工时数为 17 天。
 |
（理）曲线（）与直线的交点坐标是（
）。
9．在集合
中任取一个元素，其恰好满足三角方程
的概率为 
。（用分数作答）
10．设直线与直线的夹角为，则
，若直线与的夹角为
，则 
。
11．对于正数和，其中，定义，其中
是满足的最大整数，则
。
12．如图（1）所示，三棱锥S—ABC被平行于底面的平面所截，得到三棱锥S—DEF，则
棱锥的体积之比为
。如图（2）所示，将上述真命
题加以推广，即要求得到更一般的真命题，而已知的命题应成为所推广命题的一个特例，
推广的命题为：三棱锥S—ABC被一平面所截，得到三棱锥S—PQR，则棱锥的体积之
比为
。
二、选择题（每题4分，共16分）
13．已知，则在上的射影为
（ C
）
（A） ； （B） 
； （C） 
； （D） 
14．右图是正方体的平面展开图，在这个正方体中，
① BM与ED平行；
② CN与BE是异面直线；
③ CN与BM成60°；
④ DM与BN垂直。
以上四个命题中，正确命题的序号是 （ C ）
（A） ①②③ （B） ②④ （C） ③④ （D） ②③④
15．函数
的奇偶性是
（ A ）
（A）奇非偶（B）偶非奇 （C）既奇又偶 （D 非奇非偶
16．四面体的顶点和各棱中点共10个点，在其中取4个不共面的点，不同的取法共有（ D ）
（A） 150种 （B） 147种 （C） 144种 （D） 141种
三、解答题：（12分+12分+16分+16分，共56分）
17．、、为的三个内角，已知是
中项的系数，且
，求、、。
解：设含的项为
，
，项的系数为
，∴
，∵，由正弦定理，得 
，
∴是直角三角形，∴
18．已知︱︱是、的夹角，为何值时，
为最大角，并求此时的坐标。
解：︱︱
，
显见 
时，
，此时与方向相反，
设
，∴
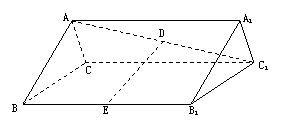19．如图，在正三棱柱ABC—A1B1C1中，各棱长都相等，D，E分别为AC1，BB1的中点.
（1）求证：DE//平面A1B1C1；
（2）求二面角A1—DE—B1的大小.
解：（1）取A1C1中点F，连结B1F，DF，
∵D，E分别为AC1和BB1的中点，
∴DF//AA1，DF=
AA1
B1E//AA1，B1E=AA1，∴DF//B1E，DF=B1E，∴DEB1F为平行四边形，………2分
∴DE//B1F，又∵B1F
平面A1B1C1，DE
平面A1B1C1，∴DE//平面A1B1C1.……4分
（2）连结A1D，A1E，在正三棱柱ABC—A1B1C1中，∵平面A1B1C1⊥平面ACC1A1，A1C1是平面
A1B1C1与平面ACC1A1的交线，又∵B1F平面A1B1C1，且B1F⊥A1C1，∴B1F⊥平面ACC1A1，
又DE//B1F，∴DE⊥平面ACC1A1，∴∠FDA1为二面角A1—DE—B1的平面角，……8分
并且∠FDA1=∠A1DC1，设正三棱柱的棱长为1，∵∠AA1C1=90°，D是AC1中点，
∴DC1=
，A1D=，∠A1DC1=90°∴∠FDA1=45°，即二面角A1—DE—B1为45°，12分
20．已知是定义在上的恒不为零的函数，且对于任意的、都满足：
（1）求的值，并证明对任意的，都有；
（2）设当时，都有，证明在上是减函数；
（3）设时，
表示数列的前项和，
（文）求；
（理）在（2）的条件下，求集合中的最大
元素和最小元素。
解：（1）
，
（2）∵当时，都有
，∴当
，即
时，有
， 即
，
，∴在上是减函数。
（3）（文）
∴
（理）∵在上是减函数，{
}是递增数列，∴数列
是递减
数列。∴集合中的最大元素为
，最小元素为
。