高考解析几何
一)选择题
1. (2004.江苏)若双曲线![]() 的一条准线与抛物线
的一条准线与抛物线![]() 的准线重合,则双曲线离心率为 ( A )
的准线重合,则双曲线离心率为 ( A )
(A)![]() (B)
(B)![]() (C) 4
(D)
(C) 4
(D)![]()
2.(2004.全国理)椭圆![]() 的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点
的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点
为P,则![]() = ( C )
= ( C )
A.![]() B.
B.![]() C.
C.![]() D.4
D.4
3.(2004.全国理)设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l
的斜率的取值范围是 ( C )
A.[-![]() ,
,![]() ] B.[-2,2] C.[-1,1] D.[-4,4]
] B.[-2,2] C.[-1,1] D.[-4,4]
4.(2004.湖北理)与直线![]() 的平行的抛物线
的平行的抛物线![]() 的切线方程是 ( D
)
的切线方程是 ( D
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.(2004.湖北理)已知椭圆![]() 的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为 ( D )
的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为 ( D )
A.![]() B.3 C.
B.3 C.![]() D.
D.![]()
6.(2004. 福建理)已知F1、F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A、B两点,若△ABF2是真正三角形,则这个椭圆的离心率是( A )
A.![]()
![]() B.
B.![]() C.
C.![]() D.
D.![]()
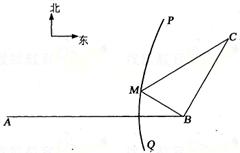 7.(2004. 福建理)如图,B地在A地的正东方向4 km处,C
7.(2004. 福建理)如图,B地在A地的正东方向4 km处,C
地在B地的北偏东30°方向2 km处,河流
的没岸PQ(曲线)上任意一点到A的距离
比到B的距离远2 km.现要在曲线PQ上
选一处M建一座码头,向B、C两地转运
货物.经测算,从M到B、M到C修建公
路的费用分别是a万元/km、2a万元/km,
那么修建这两条公路的总费用最低是( B )
A.(2![]() -2)a万元 B.5a万元
-2)a万元 B.5a万元
C.(2![]() +1)
a万元 D.(2
+1)
a万元 D.(2![]() +3)
a万元
+3)
a万元
8.(2004. 重庆理)圆![]() 的圆心到直线
的圆心到直线![]() 的距离为 ( D )
的距离为 ( D )
A.2 B.![]() C.1
D.
C.1
D.![]()
9.(2004. 重庆理)已知双曲线![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,点P在双曲线的右支上,且
,点P在双曲线的右支上,且![]() ,则此双曲线的离心率e的最大值为: ( B )
,则此双曲线的离心率e的最大值为: ( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.(2004. 辽宁卷)已知点![]() 、
、![]() ,动点
,动点![]() ,则点P的轨迹是D
,则点P的轨迹是D
A.圆 B.椭圆 C.双曲线 D.抛物线
10.(2004. 辽宁卷)已知点![]() 、
、![]() ,动点P满足
,动点P满足![]() . 当点P的纵坐标是
. 当点P的纵坐标是![]() 时, 点P到坐标原点的距离是A
时, 点P到坐标原点的距离是A
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
11.(2004.湖南理)如果双曲线![]() 上一点P到右焦点的距离等于
上一点P到右焦点的距离等于![]() ,那么点P到右准线的距离是 ( A )
,那么点P到右准线的距离是 ( A )
A.![]() B.13 C.5 D.
B.13 C.5 D.![]()
12、(2004. 四川理)已知圆C与圆(x-1)2+y2=1关于直线y=-x对称,则圆C的方程为( C )
A (x+1)2+y2=1 B x2+y2=1 C x2+(y+1)2=1 D x2+(y-1)2=1
13、(2004. 四川理)在坐标平面内,与点A(1,2)的距离为1,且与点B(3,1)的距离为2的直线共有( B )
A 1条 B 2条 C 3条 D 4条
14.(7) (2004. 天津卷)若![]() 为圆
为圆![]() 的弦AB的中点,则直线AB的方程是(A)
的弦AB的中点,则直线AB的方程是(A)
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
15、(2004. 人教版理科)圆![]() 在点
在点![]() 处的切线方程为( )
处的切线方程为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
16、(2004. 人教版理科)设双曲线的焦点在![]() 轴上,两条渐近线为
轴上,两条渐近线为![]() ,则该双曲线的离心率
,则该双曲线的离心率![]() ( )
( )
A、![]() B、
B、 ![]() C、
C、![]() D、
D、![]()
17) (2004. 天津卷)设P是双曲线![]() 上一点,双曲线的一条渐近线方程为
上一点,双曲线的一条渐近线方程为![]() ,
,![]() 、
、![]() 分别是双曲线的左、右焦点。若
分别是双曲线的左、右焦点。若![]() ,则
,则![]() (C)
(C)
(A)
![]() 或
或![]() (B)
6 (C) 7 (D)9
(B)
6 (C) 7 (D)9
二)填空题
11.(2004. 辽宁卷)若经过点P(-1,0)的直线与圆![]() 相切,则此直线在y轴上的截距是 1
.
相切,则此直线在y轴上的截距是 1
.
12.(04. 上海春季高考)过抛物线![]() 的焦点
的焦点![]() 作垂直于
作垂直于![]() 轴的直线,交抛物线于
轴的直线,交抛物线于![]() 、
、![]() 两点,则以
两点,则以![]() 为圆心、
为圆心、
![]() 为直径的圆方程是________________.
为直径的圆方程是________________.![]()
13.(2004. 辽宁卷)若经过点P(-1,0)的直线与圆![]() 相切,则此直线在y轴上的截距是 1
.
相切,则此直线在y轴上的截距是 1
.
14.(04. 上海春季高考)过抛物线![]() 的焦点
的焦点![]() 作垂直于
作垂直于![]() 轴的直线,交抛物线于
轴的直线,交抛物线于![]() 、
、![]() 两点,则以
两点,则以![]() 为圆心、
为圆心、
![]() 为直径的圆方程是________________.
为直径的圆方程是________________.![]()
15.(2004. 重庆理)对任意实数K,直线:![]() 与椭圆:
与椭圆: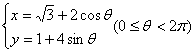 恒有公共点,则b取值范围是______
[-1,3]_________
恒有公共点,则b取值范围是______
[-1,3]_________
16.(2004. 福建理)直线x+2y=0被曲线x2+y2-6x-2y-15=0所截得的弦长等于 4![]() .
.
17.(04. 上海春季高考)若平移椭圆![]() ,使平移后的椭圆中心在第一象限,且它与
,使平移后的椭圆中心在第一象限,且它与![]() 轴、
轴、![]() 轴分别只有一个交点,则平移后的椭圆方程是______
轴分别只有一个交点,则平移后的椭圆方程是______![]() _____________.
_____________.
18.(04. 上海春季高考)若平移椭圆![]() ,使平移后的椭圆中心在第一象限,且它与
,使平移后的椭圆中心在第一象限,且它与![]() 轴、
轴、![]() 轴分别只有一个交点,则平移后的椭圆方程是______
轴分别只有一个交点,则平移后的椭圆方程是______![]() _____________.
_____________.
19(2004.湖南理)设F是椭圆![]() 的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使FP1,FP2,FP3,…组成公差为d的等差数列,则d的取值范围为
的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使FP1,FP2,FP3,…组成公差为d的等差数列,则d的取值范围为 ![]() .
.
20、(2004. 人教版理科)设![]() 是曲线
是曲线![]() 上的一个动点,则点
上的一个动点,则点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到
到![]() 轴的距离之和的最小值为
.
轴的距离之和的最小值为
.
21.以点(1,2)为圆心,与直线4x+3y-35=0相切的圆的方程是________________.![]()
22、(2004. 四川理)设x,y满足约束条件: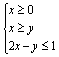 ,则z=3x+2y的最大值是
5 。
,则z=3x+2y的最大值是
5 。
23、(2004.
四川理)设中心在原点的椭圆与双曲线2x2-2y2=1有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是
。(![]() )
)
24.
(2004. 天津卷)如果过两点![]() 和
和![]() 的直线与抛物线
的直线与抛物线![]() 没有交点,那么实数
没有交点,那么实数![]() 的取值范围是__________________
的取值范围是__________________ ![]()
25、(2004.上海理)设抛物线的顶点坐标为(2,0),准线方程为x=-1,则它的焦点坐标为 (5,0) .
26、圆心在直线2x-y-7=0上的圆C与y轴交于两点A(0, -4),B(0, -2),则圆C的方程为 (x-2)2+(y+3)2=5 .
27、(2004.上海理)教材中“坐标平面上的直线”与“圆锥曲线”两章内容体现出解析几何的本质是 用代数的方法研究图形的几何性质 .
| 28、(2004. 上海卷文科)当x、y满足不等式组 |
| 时,目标函数k=3x-2y的最大值为6 . |
| y≥3 | ||
| x+y≤8 |
29、(2004. 上海卷文科)圆心在直线x=2上的圆C与y轴交于两点A(0, -4),B(0, -2),则圆C的方程为 (x-2)2+(y+3)2=5 .
三)解答题
30.(2004. 辽宁卷)(本小题满分12分)
设椭圆方程为![]() ,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,
,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,
点P满足![]() ,点N的坐标为
,点N的坐标为![]() ,当l绕点M旋转时,求:
,当l绕点M旋转时,求:
(1)动点P的轨迹方程;
(2)![]() 的最小值与最大值.
的最小值与最大值.
30.本小题主要考查平面向量的概念、直线方程的求法、椭圆的方程和性质等基础知识,以及轨迹的求法与应用、曲线与方程的关系等解析几何的基本思想和综合解题能力. 满分12分.
(1)解法一:直线l过点M(0,1)设其斜率为k,则l的方程为![]()
记![]() 、
、![]() 由题设可得点A、B的坐标
由题设可得点A、B的坐标![]() 、
、![]() 是方程组
是方程组
|
|
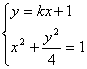 的解.…………………………2分
的解.…………………………2分
将①代入②并化简得,![]() ,所以
,所以
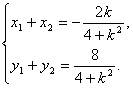 于是
于是
![]() …………6分
…………6分
设点P的坐标为![]() 则
则
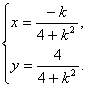 消去参数k得
消去参数k得![]() ③
③
当k不存在时,A、B中点为坐标原点(0,0),也满足方程③,所以点P的轨迹方
程为![]() ………………8分
………………8分
解法二:设点P的坐标为![]() ,因
,因![]() 、
、![]() 在椭圆上,所以
在椭圆上,所以
![]() ④
④
![]() ⑤
⑤
④—⑤得![]() ,所以
,所以
![]()
当![]() 时,有
时,有![]() ⑥
⑥
并且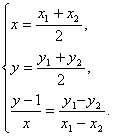 ⑦ 将⑦代入⑥并整理得
⑦ 将⑦代入⑥并整理得 ![]() ⑧
⑧
当![]() 时,点A、B的坐标为(0,2)、(0,-2),这时点P的坐标为(0,0)
时,点A、B的坐标为(0,2)、(0,-2),这时点P的坐标为(0,0)
也满足⑧,所以点P的轨迹方程为
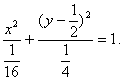 ………………8分
………………8分
(2)解:由点P的轨迹方程知![]() 所以
所以
![]() ……10分
……10分
故当![]() ,
,![]() 取得最小值,最小值为
取得最小值,最小值为![]() 时,
时,![]() 取得最大值,
取得最大值,
最大值为![]() ……………………12分
……………………12分
注:若将![]() 代入
代入![]() 的表达式求解,可参照上述标准给分.
的表达式求解,可参照上述标准给分.
31.(2004.湖南理)(本小题满分12分)
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.
(I)设点P分有向线段![]() 所成的比为
所成的比为![]() ,证明:
,证明:![]()
![]() ;
;
(II)设直线AB的方程是x-2y+12=0,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
31.解:(Ⅰ)依题意,可设直线AB的方程为 ![]() 代入抛物线方程
代入抛物线方程![]() 得
得
![]() ①
①
设A、B两点的坐标分别是 ![]() 、
、![]() 、x2是方程①的两根.
、x2是方程①的两根.
所以 ![]()
由点P(0,m)分有向线段![]() 所成的比为
所成的比为![]() ,
,
得![]()
又点Q是点P关于原点的对称点,
故点Q的坐标是(0,-m),从而![]() .
.
![]()
![]()
![]()
![]()
所以 ![]()
(Ⅱ)由 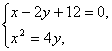 得点A、B的坐标分别是(6,9)、(-4,4).
得点A、B的坐标分别是(6,9)、(-4,4).
由 ![]() 得
得 ![]()
所以抛物线 ![]() 在点A处切线的斜率为
在点A处切线的斜率为 ![]()
设圆C的方程是![]()
则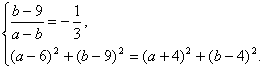
解之得 ![]()
所以圆C的方程是 ![]()
即 ![]()
32.(2004. 天津卷)(本小题满分14分)
椭圆的中心是原点O,它的短轴长为![]() ,相应于焦点
,相应于焦点![]() 的准线
的准线![]() 与
与![]() 轴相交于点A,
轴相交于点A,![]() ,过点A的直线与椭圆相交于P、Q两点。
,过点A的直线与椭圆相交于P、Q两点。
(I) 求椭圆的方程及离心率;
(II)若![]() 求直线PQ的方程;
求直线PQ的方程;
(III)设![]() ,过点P且平行于准线
,过点P且平行于准线![]() 的直线与椭圆相交于另一点M,证明
的直线与椭圆相交于另一点M,证明
![]() 。
。
(22)本小题主要考查椭圆的标准方程和几何性质,直线方程,平面向量的计算,曲线和方程的关系等解析几何的基本思想方法和综合解题能力。满分14分。
(I)解:由题意,可设椭圆的方程为![]()
由已知得
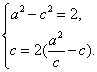
解得 ![]()
所以椭圆的方程为![]() ,离心率
,离心率![]() 。。。。。。。。。。。。。。。。。。。。。4分
。。。。。。。。。。。。。。。。。。。。。4分
(II)解: 由(I)可得![]()
设直线PQ的方程为![]() 由方程组
由方程组
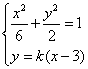
得
![]()
依题意 ![]() 得
得
![]()
设 ![]() 则
则
![]() ①
①
![]() ②
②
由直线PQ的方程得 ![]() 于是
于是
![]() ③
③
![]() ④
。。。。。。。。。。。。。。。。。。。。。8分
④
。。。。。。。。。。。。。。。。。。。。。8分
由①②③④得![]() 从而
从而![]()
所以直线PQ的方程为
![]() 或
或![]() 。。。。。。。。。。。。。。。。。。。10分
。。。。。。。。。。。。。。。。。。。10分
(III)证明:![]() 由已知得方程组
由已知得方程组
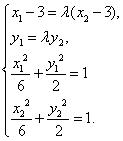
注意![]() 解得
解得 ![]() 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。12分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。12分
因![]() 故
故
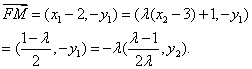
而![]() 所以
所以
![]() 。。。。。。。。。。。。。。。。。。。。。。。。。。。14分
。。。。。。。。。。。。。。。。。。。。。。。。。。。14分
33.制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.
某投资人打算投资甲、乙两个项目. 根据预测,甲、乙项目可能的最大盈利率分别为100﹪和50﹪,可能的最大亏损分别为30﹪和10﹪. 投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
33、解:![]() ,设
,设![]()
当![]() 时,
时,![]() 取最大值7万元
取最大值7万元
34.(2004.江苏)已知椭圆的中心在原点,离心率为,一个焦点是F(-m,0)(m是大于0的常数). (Ⅰ)求椭圆的方程;
(Ⅱ)设Q是椭圆上的一点,且过点F、Q的直线![]() 与y轴交于点M. 若
与y轴交于点M. 若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
35、解:(1)![]()
(2)![]() 或0
或0
36.(2004. 福建理)(本小题满分12分)
如图,P是抛物线C:y=![]() x2上一点,直线l过点P且与抛物线C交于另一点Q.
x2上一点,直线l过点P且与抛物线C交于另一点Q.
(Ⅰ)若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程;
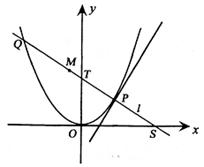 (Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求
(Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求![]() 的取值范围.
的取值范围.
37. 本题主要考查直线、抛物线、不等式等基础知识,求轨迹方程的方法,解析几何的基本思想和综合解题能力.满分12分.
解:(Ⅰ)设P(x1,y1),Q(x2,y2),M(x0,y0),依题意x1≠0,y1>0,y2>0.
由y=![]() x2,
①
x2,
①
得y'=x.
∴过点P的切线的斜率k切= x1,
∴直线l的斜率kl=-![]() =-
=-![]() ,
,
∴直线l的方程为y-![]() x12=-
x12=-![]() (x-x1),
(x-x1),
方法一:
联立①②消去y,得x2+![]() x-x12-2=0.
x-x12-2=0.
∵M是PQ的中点
![]() x0=
x0=![]() =-
=-![]() ,
,
∴
y0=![]() x12-
x12-![]() (x0-x1).
(x0-x1).
消去x1,得y0=x02+![]() +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+![]() +1(x≠0).
+1(x≠0).
方法二:
由y1=![]() x12,y2=
x12,y2=![]() x22,x0=
x22,x0=![]() ,
,
得y1-y2=![]() x12-
x12-![]() x22=
x22=![]() (x1+x2)(x1-x2)=x0(x1-x2),
(x1+x2)(x1-x2)=x0(x1-x2),
则x0=![]() =kl=-
=kl=-![]() ,
,
∴x1=-![]() ,
,
将上式代入②并整理,得
y0=x02+![]() +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+![]() +1(x≠0).
+1(x≠0).
(Ⅱ)设直线l:y=kx+b,依题意k≠0,b≠0,则T(0,b).
分别过P、Q作PP'⊥x轴,'⊥y轴,垂足分别为P'、Q',则
![]()
![]() .
.
![]() y=
y=![]() x2
x2
由 消去x,得y2-2(k2+b)y+b2=0. ③
y=kx+b
![]() y1+y2=2(k2+b),
y1+y2=2(k2+b),
则
y1y2=b2.
方法一:
∴![]() b(
b(![]() )≥2b
)≥2b![]() =2b
=2b![]() =2.
=2.
∵y1、y2可取一切不相等的正数,
∴![]() 的取值范围是(2,+
的取值范围是(2,+![]() ).
).
方法二:
∴![]() =b
=b![]() =b
=b![]() .
.
当b>0时,![]() =b
=b![]() =
=![]() =
=![]() +2>2;
+2>2;
当b<0时,![]() =-b
=-b![]() =
=![]() .
.
又由方程③有两个相异实根,得△=4(k2+b)2-4b2=4k2(k2+2b)>0,
于是k2+2b>0,即k2>-2b.
所以![]() >
>![]() =2.
=2.
∵当b>0时,![]() 可取一切正数,
可取一切正数,
∴![]() 的取值范围是(2,+
的取值范围是(2,+![]() ).
).
方法三:
由P、Q、T三点共线得kTQ=KTP,
即![]() =
=![]() .
.
则x1y2-bx1=x2y1-bx2,即b(x2-x1)=(x2y1-x1y2).
于是b=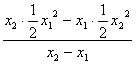 =-
=-![]() x1x2.
x1x2.
|
|
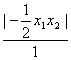 +
+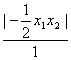 =
=∵![]() 可取一切不等于1的正数,
可取一切不等于1的正数,
∴![]() 的取值范围是(2,+
的取值范围是(2,+![]() ).
).
38.(2004.湖北理)(本小题满分12分)
直线![]() 的右支交于不同的两点A、B.
的右支交于不同的两点A、B.
(I)求实数k的取值范围;
(II)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
38.本小题主要考查直线、双曲线的方程和性质,曲线与方程的关系,及其综合应用能力,满分12分.
解:(Ⅰ)将直线![]()
![]() ……①
……①
依题意,直线l与双曲线C的右支交于不同两点,故

(Ⅱ)设A、B两点的坐标分别为![]() 、
、![]() ,则由①式得
,则由①式得
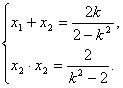 ……②
……②
假设存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F(c,0).
则由FA⊥FB得:
![]()
整理得
![]() ……③
……③
把②式及![]() 代入③式化简得
代入③式化简得
![]()
解得![]()
可知![]() 使得以线段AB为直径的圆经过双曲线C的右焦点
使得以线段AB为直径的圆经过双曲线C的右焦点
39. (04. 上海春季高考)(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知倾斜角为![]() 的直线
的直线![]() 过点
过点![]() 和点
和点![]() ,
,![]() 在第一象限,
在第一象限,![]() .
.
(1) 求点![]() 的坐标;
的坐标;
(2) 若直线![]() 与双曲线
与双曲线![]()
![]() 相交于
相交于![]() 、
、![]() 两点,且线段
两点,且线段![]() 的中点坐标为
的中点坐标为![]() ,求
,求![]() 的值;
的值;
(3) 对于平面上任一点![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,称
上运动时,称![]() 的最小值为
的最小值为![]() 与线段
与线段![]() 的距离. 已知点
的距离. 已知点![]() 在
在![]() 轴上运动,写出点
轴上运动,写出点![]() 到线段
到线段![]() 的距离
的距离![]() 关于
关于![]() 的函数关系式.
的函数关系式.
39. (1)
直线![]() 方程为
方程为![]() ,设点
,设点![]() ,由
,由![]() 及
及![]() ,
,![]() 得
得![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() 。
。
(2)由![]() 得
得![]() ,设
,设![]() ,则
,则![]() ,得
,得![]() 。
。
(3)(解法一)设线段![]() 上任意一点
上任意一点![]() 坐标为
坐标为![]() ,
,![]() ,
,
记![]()
![]() ,
,
当![]() 时,即
时,即![]() 时,
时,![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ;
;
 当
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() 。
。
综上所述,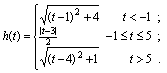
(解法二) 过![]() 、
、![]() 两点分别作线段
两点分别作线段![]() 的垂线,交
的垂线,交![]() 轴于
轴于![]() 、
、![]() ,
,
当点![]() 在线段
在线段![]() 上,即
上,即![]() 时,由点到直线的距离公式得:
时,由点到直线的距离公式得:![]() ;
;
当点![]() 的点在点
的点在点![]() 的左边,
的左边,![]() 时,
时,![]() ;
;
当点![]() 的点在点
的点在点![]() 的右边,
的右边,![]() 时,
时,![]() 。
。
综上所述,