| 班级 | 姓名 | 学号 | 时间 | |||||
| 课题 | 空间的两条直线及异面直线 | 设计 | ||||||
| 一、 知识点击 1.掌握空间两直线的位置关系,平行公理,异面直线的定义、性质和判定。 2. 掌握异面直线所成角和距离的概念与求法,求异面直线所成的角常采用“平移转化法”,异面直线的距离,只要求会计算已给出共垂线时的距离。 3. 理解并熟悉反证法的证题思路与步骤,会用反证法证明一些简单的问题。 二、 智能达标 1.已知异面直线a.b所成的角为50 A. 1条 B. 2条 C. 3条 D. 4条 2.棱长为1的正方体ABCD—A A. 3.在正三棱柱ABC—A A. 60 4.直线a, b, c两两垂直,且互为异面直线,若直线d是b、c的共垂线,则a和d是 ( B ) A. 重合直线 B平行直线 C相交直线 D 异面直线 5在空间四边形ABCD中,E. F分别为AB、 CD的中点,若AD=BC且AD与BC成60 6.如图是一个正方体的展开图,在原正方体中有下列命题 ⑴AB与EF所在直线平行
⑶MN与BA所在直线成60度角 F ⑷MN与CD所在直线互相垂直 C B 其中正确的命题的序号为 3,4 E N A M | ||||||||
| 7.如图,三棱台ABC—A (1) 求证:BC⊥A1B, BC⊥A1A, A1A⊥A1B, (2) 求异面直线AA1与BC的距离。
C1 A1
B C A 8、已知:直线a,b异面,a上两点A、B距离为8,b上两点距离为6,AD、BC的中点分别为M、N且 求证:a⊥b
A
M B N
D C b |
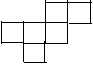 ⑵AB与CD所在直线平行 D
⑵AB与CD所在直线平行 D 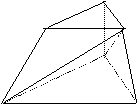 B1
B1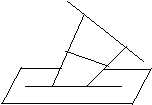 a
a