| 班级 | 姓名 | 学号 | 时间 | |||||||
| 课题 | 棱柱、棱锥侧面积与体积 | 设计 | ||||||||
| 一、方法点击: 1、 棱柱、棱锥的概念及性质是计算中必不可少的依据,在有关计算中要充分利用他们。 2、 多面体中的截面及棱锥直角三角形和直角梯形是将空间问题平面化的重要途径。 3、 平行于底面的截面分高的比与面积比、体积比的关系也是解题的一重要线索。 4、 求体积常用的方法:公式法、转移法、割补法等,注意等体积法在求点面距离中的重要应用。 二、知能达标: 1、已知正三棱柱ABC—A 1B 1C1的底面边长为2cm,高为4cm,过BC作一截面,使截面与底面成60°角,则截面面积为 ( B ) A 4cm2 B 2、正三棱锥侧面积是底面积的2倍,那么侧面与底面所成的二面角是 ( C ) A 30° B 45° C 60° D 75° 3、把等腰直角三角形ABC沿斜边上的高AD折成直二面角B—AD—C,则BD与面ABC所成角的正切值为 ( B ) A
∠APB=∠BPC=∠CPA=40°,过点A作截面 AEF,分别交PB,PC于E,F,则截面△AEF周长的 E F 最小值为 ( A ) A 6 B 5、正三棱锥的侧棱与底面所成角的正切值为 则棱锥的侧面积与全面积之比为 3:4 。 B 6、已知斜三棱柱ABC—A 1B 1C1各条棱长都是a,且一个顶点A1在另一底面的射影恰好是这底面正三角形的中心,求此三棱柱的全面积。
| ||||||||||
| 7、在斜三棱柱ABC-A1B1C1中,每条棱长都为a,侧棱长与底面所成的角等于 垂直于底面,求四棱锥C1-ABB1A1的体积.
8、如图,四棱锥S-ABCD的底面ABCD是边长为a的正方形,SD⊥面ABCD,面ABEF与侧面SCD交于EF,二面角S-AB-C为 (2)棱锥S-ABEF的体积. |
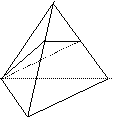 4、如图,在棱长为
4、如图,在棱长为