| 班级 | 姓名 | 学号 | 时间 | |||||||
| 课题 | 棱柱、棱锥有关概念及性质 | 设计 | ||||||||
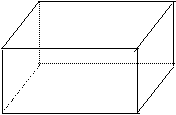
| 一、方法点击: 1、 棱柱、棱锥有关概念及性质是解决多面体问题的基础,必须熟练掌握。 2、 第一章的有关点、线、面之间的位置关系(主要是平行、垂直关系)和数量关系也是空间几何体的主要的研究对象,这些知识有助于多面体的有关问题的解决。 二、知能达标: 1、一个棱锥是正四棱锥的充分不必要条件是 ( ) A、 各侧面与底面成相等的二面角 B、 各侧面是等腰三角形,且底面是正方形 C、 各侧面是正三角形 D、 各侧棱与底面成相等的角 2、棱柱成为直棱柱的一个必要而不充分条件是 ( ) A、棱柱有一条侧棱与底面垂直 B、棱柱有一条侧棱与底面的两条边垂直 C、棱柱有一个侧面与底面的一条边垂直 E、 棱柱有一个侧面是矩形且与底面垂直 3、有一正棱锥的底面边长与侧棱的长相等,则这个棱锥一定不是 ( ) A、三棱锥 B、 四棱锥 C、五棱锥 D、六棱锥 4、在三棱锥A—BCD中,AC=BD,AD=BC,AB=CD,三个侧面与底面所成的二面角分别为 5、已知长方体ABCD—A 1B 1C1 D1中,棱长AA1=5,AB=12,求直线B1 C1和平面A1 BCD1的距离。
A1 B1 D C A B | ||||||||||
| 8、四面体P—ABC中,已知PA=3,PB=PC=2,∠APB=∠BPC=∠CPA=60°,求证:(1)PA⊥BC;(2)平面PBC⊥平面ABC
A C
B 9、已知,斜三棱柱ABC—A 1B 1C1,在底面△ABC中,A=30°,C=90°,BC=1,侧面A 1ACC1⊥底面ABC,侧棱与底面成60°的角,AA1= |
 D1 C1
D1 C1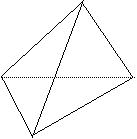 P
P