| 班级 | 姓名 | 学号 | 时间 | |||||||
| 课题 | 棱柱、棱锥、棱台的侧面积与体积 | 设计 | ||||||||
| 一、方法点击: 1、 棱柱、棱锥、棱台的概念及性质是计算中必不可少的依据,在有关计算中要充分利用他们。 2、 多面体中的截面及棱锥、棱台的直角三角形和直角梯形是将空间问题平面化的重要途径。 3、 对于棱台有时采用“还台为锥”的方法可使问题得以解决。 4、 平行于底面的截面分高的比与面积比、体积比的关系也是解题的一重要线索。 5、 求体积常用的方法:公式法、转移法、割补法等,注意等体积法在求点面距离中的重要应用。 二、知能达标: 1、已知正三棱柱ABC—A 1B 1C1的底面边长为2cm,高为4cm,过BC作一截面,使截面与底面成60°角,则截面面积为 ( B ) A 4cm2 B 2、正三棱锥侧面积是底面积的2倍,那么侧面与底面所成的二面角是 ( C ) A 30° B 45° C 60° D 75° 3、把等腰直角三角形ABC沿斜边上的高AD折成直二面角B—AD—C,则BD与面ABC所成角的正切值为 ( B ) A
∠APB=∠BPC=∠CPA=40°,过点A作截面 AEF,分别交PB,PC于E,F,则截面△AEF周长的 E F 最小值为 ( A ) A 6 B 5、正三棱锥的侧棱与底面所成角的正切值为 则棱锥的侧面积与全面积之比为 3:4 。 B 6、正四棱台的上、下底面边长分别是方程x2-9x+18=0的两根,其侧面积等于两底面积之和,则其斜高= 2.2 ;高= 2 。 7、已知斜三棱柱ABC—A 1B 1C1各条棱长都是a,且一个顶点A1在另一底面的射影恰好是这底面正三角形的中心,求此三棱柱的全面积。
| ||||||||||
|
|
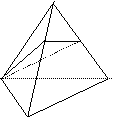 4、如图,在棱长为
4、如图,在棱长为