| 姓名 | 班 级 | 学 号 | 时 间 | ||||
| 课题 | 函数的图象 | 设 计 |
| ||||
| 一、方法点拨: 1、 掌握基本初等函数的图象特征。主要指掌握一次函数、二次函数、指数函数与对数函数、三角函数的图象特征。能利用函数的图象研究函数的性质。 2、 掌握作函数图象的基本方法:描点法和图象变换法(平移、伸缩、对称)。 3、 函数图象从“形”的方面反映了函数的变化规律,因此要能运用数形结合的思想方法解决有关问题。 二、知能达标: 1、 将f(x)=lg(1-x)的图象沿X轴向左平移1个单位,再关于Y轴对称所得的函数解析式为 2、 y= 3、 f(x)的图象过点(0,1),则f(4-x)的反函数的图象过点( ) A.(3,0) B.(0,3) C.(4,1) D.(1,4) 4、 直线y=x+b与函数y= 5、 方程lgx=cosx的实根个数为 6、 函数y=x-3+2+x,x 7、 已知f(x)= | |||||||
| 8、作出下列函数的简图: (1)y=log (3)y=2x; (4)y=elnx。 9、奇函数f(x)的定义域是R,当x>0时,f(x)= - x2+2x+2,求f(x)在R上的表达式,且作出f(x)的图象。 10、试讨论方程1-x=kx的实数根的个数。 |
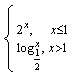 ,试作出f(x)的草图。
,试作出f(x)的草图。