高三数学统练十立体几何（2）
班级 学号 姓名
一、选择题（每小题5分，共40分）
1．对于直线
、
和平面
、
，
的一个充分条件是（ ）
∥，
，
，∥，∥
，
，
∥，，
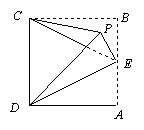
2．如图，正方形
的边长为
，
是
的中点，沿
、
分别把
、
折起，使
与
重合，重合后的点记为
，则到平面
的距离为（ ）
3．二面角
的大小为
，
，在内的射影为，在内的射影为
，则、到的距离之比为（ ）
4．在矩形中，
，
，是
的中点，沿
、
折起，使、重合为
，则直线
与平面
所成的角的余弦为（ ）
5．已知直线
平面，直线
平面，给出下列命题：①∥
；②
∥；③
∥
；④
∥．其中真命题的个数是（ ）
个
个 
个 
6．平行四边形的四个顶点在平面的同侧，、、到的距离分别为、、
，则顶点
到的距离为（ ）
7．已知
是平面的一条斜线，，线段
，
，点到平面的距离为，设
，则（ ）
≤
≥
8．已知三棱锥
的三个侧面与底面全等，且
，
，则以为棱，以
和
为面的二面角的余弦值为（ ）
二、填空题（每小题5分，共30分）
9．在
的二面角的一个面内有一条直线与二面角的棱成角，则此直线与二面角的另一个面所成角的正弦值为
．
10．如图，、
分别为两个正方形，
为
的中点，沿将正方形、折成
的二面角，则折后
与
所成角的余弦值为
．
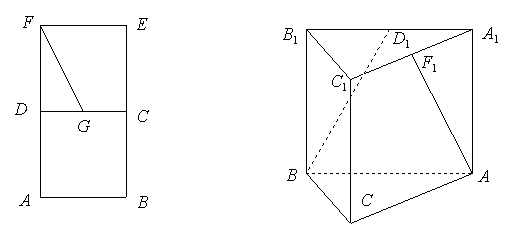
第10题图 第12题图
11．在三棱锥
中，
，
，则二面角
的余弦值为
．
12．如图，
是直三棱柱，
，点
、
分别是
、
的中点．若
，则
与
所成角的余弦是
．
13．如图所示，已知异面直线、
的公垂线段的长为
，
，
，
．若、所成的角为，则点
到直线的距离为
．
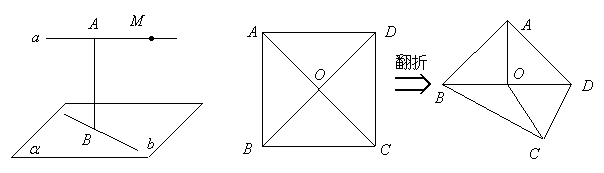
第13题图 第14题图
14．已知正方形，
、
相交于点
．若将正方形沿对角线折成的二面角，并给出下面四个结论：
①
；②
；③
为正三角形；④
．
其中，正确命题的序号是 ．
（反面有题）
三、解答题（每题15分，共30分）
15．如图，在四棱锥
中，底面是平行四边形，
底面，且
，
，
．
(Ⅰ)求证：平面
平面
；
(Ⅱ)求异面直线
与所成角的余弦值；
(Ⅲ)设二面角
的大小为
，求tg的值．
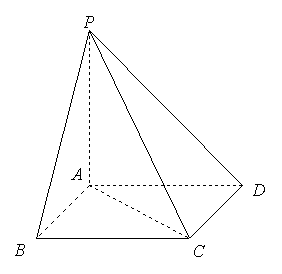
16．如图所示，直三棱柱中，
，
，
．
(Ⅰ)求点到平面
的距离；
(Ⅱ)求直线
与平面所成角的正切值；
(Ⅲ)求以与
为半平面的二面角的正切值．
参考答案
1—4：
；5—8：
。
9．
； 10．
； 11．
； 12．
； 13．
； 14．①④．
15．(Ⅰ)在三角形
中，
，
，，故
，故
．（……2分）
又底面，是在底面内的射影，
底面，∴
，故
平面．（4分）又平面
，∴平面平面．（……5分）
(Ⅱ)连结，交于，则为的中点，取的中点，连
，则∥，∴
就是异面直线与所成的角．（……7分）连结
，则
，
，
，由余弦定理，得
．（……10分）
(Ⅲ)∵∥，∴平面，∴
平面．过作
，垂足为，连结
，由三垂线定理知
．∴
为所求二面角的平面角．（……12分）在Rt
中，由面积关系得
，在Rt
中，tg
．（15分）
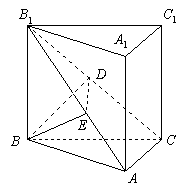
16．(Ⅰ)过作
，垂足为，容易证明
平面，故的长就是点到平面的距离．（……3分）计算得
．（…5分）(Ⅱ)由(Ⅰ)知，平面，则
就是直线与平面所成的角．（……8分）计算得tg
．（……10分）
(Ⅲ)过作
的垂线交于，连结，由(Ⅰ)知，
，则
就是所求二面角的平面角．（……13分）计算得，tg
．（……15分）