高三数学统练十一立体几何（3）
班级___________ 姓名_____________ 学号____________ 成绩___________
一、选择题（每小题5分，共40分）
1. 已知m, n是直线，
, 
, 
是平面，给出下列的命题：① m//, m//, ∩=n, 则m//n；②
⊥,⊥, 则//；③ m⊥, n⊥, m⊥n, 则⊥；④ //, //, m⊥, 则m⊥，其中错误的命题的序号是……（ ）
（A）① （B）② （C）③ （D）④
2. 将边长为a的正方形ABCD沿对角线AC折起，使得BD=a，则三棱锥D－ABC的体积是…………………………………………………………………（ ）
（A）
a3 （B）
a3 （C）
a3 （D）
a3
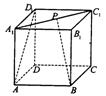
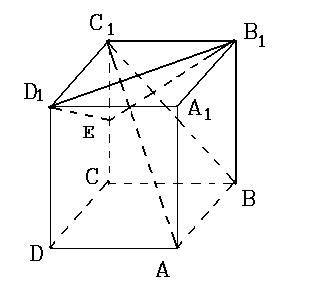
3. 如图ABCD－A1B1C1D1是正方体，点P在线段A1C1上运动，异面直线BP与AD1所成的角为θ，则θ的取值范围是………………………………… ( )
（A）0<θ<
（B）0<θ≤
（C）0<θ<
（D）0<θ≤
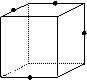
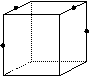
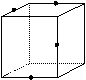
4.下列四个图形中,P,Q,R,S分别是正方体所在棱的中点,
这四个点共面的图形是…………………………………………………… ( )
（A）甲与乙 （B）乙与丙 （C）丙与丁 （D）丁与甲
（甲） (乙) （丙） （丁）
5. 如果一个圆锥中的有三条的母线两两所成的角均为60°，那么这个圆锥的侧面展开图的圆心角等于…………………………………………………（ ）
（A）π （B）
（C）
π （D）π
6．若圆锥的轴截面是一个面积为
的正三角形,那么其内切球的体积是………………………………………………………………………………( )
（A）4
（B）6
（C）
（D）
7. 等边△ABC的边长为4，将它沿平行于BC的线段PQ折起，使平面APQ⊥平面BPQC.若折叠后AB的长记为d，则d的最小值为…………………（ ）
（A）
（B）3
（C）
（D）
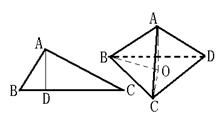
8．如图，在⊿ABC中，AB⊥AC、AD⊥BC，D是垂足，则
（射影定理）。类似有命题：“三棱锥A-BCD（图2）中，AD⊥平面ABC，AO⊥平面BCD，O为垂足，且O在⊿BCD内，则
” ，上述命题是……………………………………………………………………………（ ）
（A） 真命题
（B）
假命题
（C） 增加AB⊥AC的条件才是真命题
（D） 增加三棱锥A-BCD是正三棱锥的
条件才是真命题
二、填空题（每小题5分，共30分）
9．等腰直角三角形ABD与正三角形CBD所在平面互相垂直，∠BAD=90°,E是BC的中点，则AE与平面BCD所成的角的大小是_________.
10. 在同一桌面上,有四个半径为R的球两两相切,则放在上边的球的球心到桌面的距离为___________．
11.如图,用一个平面去截圆柱，截得的截面曲线是一个离心率为
椭圆，则这个平面与底面所成的较小的二面角的大小为 ______________ .
12.
设一个圆锥的母线长为
，底面半径等于母线长的
，那么这个圆锥的内接圆柱的侧面积的最大值是____________
.
13. 如果a、b是异面直线，给出以下四个命题:①过空间内任何一点可以作一个和a、b都平行的平面;②过直线a有且只有一个平面和b平行;③有且只有一条直线和a、b都垂直;④过空间内任何一点可以作一条直线和a、b都相交.则所有正确命题的序号是_____________.
14. 设四面体ABCD的两条对棱AB=a, CD=b，且AB⊥CD，四面体的表面积为S，则S与ab的大小关系是 .
三、解答题（第15、16题各15分）
15. 已知长方体
中，AB=BC=1，
=2，连结
，过定点
作的垂线交
于
．
(1)求证：
；(证明过程写在下一页)
(2)求二面角
的正切值；
(3)求点
到平面
的距离．
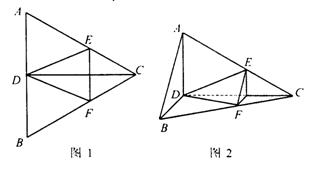
16. 如图，正△ABC的边长为2，CD是AB边上的高，E、F分别是AC和BC边上的点，且满足
，现将△ABC沿CD翻折成直二面角A－DC－B，
(1) 判断翻折后直线AB与平面DEF的位置关系并说明理由；
(2) 求二面角B－AC－D的大小；
(3) 当k为何值时，异面直线AB与DE所成角的余弦值为
，并说明理由.