高三年级五月调研考试数学试题
一、选择题
1．不等式y≤3x＋b所表示的区域恰好使点(3,4)不在此区域内，而点(4,4)在此区域内，则b的取值范围是：
A．－8≤b≤－5 B．b≤－8或b＞－5
C．－8≤b＜－5 D．b≤－8或b≥－5
2．甲：
成等比数列；
乙：lgx，lg(x+1)，lg(x+3)成等差数列。
则甲是乙的
A．充分非必要条件 B．必要非充分条件
C．充要条件 D．既非充分又非必要条件
3．已知直线
与圆
无公共点，则点
一定（ ）．
A．在圆内 B．在圆外 C．在圆上 D．都有可能
4．等差数列
与等比数列
满足:
，
，则
与
的大小关系是
A．
B．
C．
D．
5．已知f(x)=(x－a)(x－b)－2，m,n是方程f(x)=0的两根，且a＜b，m＜n，则实数a,b,m,n的大小关系是：
A．m＜a＜b＜n B．a＜m＜n＜b
C．a＜m＜b＜n D．m＜a＜n＜b
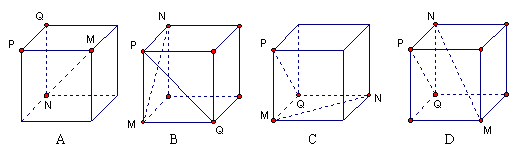
6．下列正方形中，能得出MN⊥PQ的是：
7．直线l是双曲线
的右准线，以原点为圆心且过双曲线的焦点的圆被直线l分成弧长为2比1的两段圆弧，则该双曲线的离心率是
A．
B．
C．
D．
8．函数f(x)=3ax＋1－2a在(－1，1)内不存在x0，使f(x0)=0，那么a的取值范围是：
A．a≥或a≤－1 B．a≤ C．－1≤a≤ D．a≥－1
9．在(1＋x)n=1＋a1x＋a2x2＋……＋an－1xn-1＋anxn中，若2a4=3an－6，则n的值为：
A．7 B．8 C．9 D．10
10．在等比数列{an}中，设前n项和为Sn，则 x=Sn2＋S2n2，y=Sn(S2n＋S3n)的大小关系是：
A．x＞y B．x＜y C．x=y D．为确定
11. 设
,
,
都是正实数,且,满足
,则使得
恒成立的的范围是
A. 
B. 
C. 
D. 
12．已知定义域为R的函数f（x）满足
，当x＞2时，f（x）单调递增．如果
且
，则
的值．
A．可能为0 B．恒大于0 C．恒小于0 D．可正可负
二、填空题
13．某工厂产值连续二年持续增长，已知年平均增长率P，若这二年的增长率分别为
、
，则
的最小值是________．
| ξ | 0 | 1 | 2 |
| P | 1－P |
14．设随机变量ξ的分布列为：
则ξ的数学期望Eξ的最
大值是： 。
15．前后两次民意调查显示，某竞选者第一次的支持率为46%，第二次上升到64%；第一次被调查的选民为1000人，第二次调查包括了第一次被调查者，且第一次被调查的选民在第二次调查时支持的意向没有改变，则第二次被调查者的选民总数至少是
人。
16．设s,t为非零实数，，为单位向量，若s＋t=t－s，则与的夹
角为： 。
一、选择题答题卡：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题答题卡：
13 14 15 16
三、解答题：
17．已知函数y=Asin(ωx＋Φ)(x∈R,A＞0,ω＞0)的图象在y轴右侧的第一个最高点为P(,2)，在原点右侧与x轴的第一个交点为R(，0)；
⑴求函数的解析式；⑵求函数在区间[,]上的对称轴方程。（12′）
18．箱内有大小相同的20个红球，80个黑球，从中任意取出1个，记录它的颜色后放回箱内，进行搅拌后再任意取出1个，记录它的颜色后放回箱内搅拌；假设三次都是这样抽取，试回答下列问题：（12′）
⑴求事件A：“第一次取出黑球，第二次取出红球，第三次取出黑球”的概率；
⑵求事件B：“三次中恰好有一次取出红球”的概率；
⑶如果有50人进行这样的抽取，试推测约有多少人取出2个黑球，1个红球？
19．已知数列{an}(n为正整数)是首项为a1，公比为q的等比数列：
⑴求和：a1C－a2C＋a3C；a1C－a2C＋a3C－a4C；
⑵由⑴的结果，归纳概括出关于正整数n的一个结论，并加以证明。（12′）
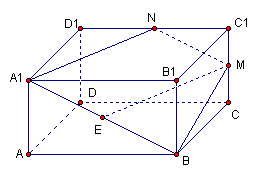
20．如图，在正四棱柱ABCD－A1B1C1D1中，A1A=AB,点E、M分别是A1B、C1C的中点，过点A1，B，M三点的平面A1BMN交C1D1于点N；
⑴求证：EM∥平面A1B1C1D1； ⑵求二面角B－A1N－B1的正切值。
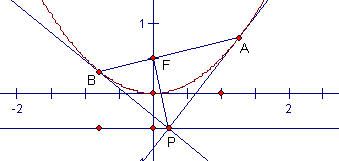
21．已知抛物线x2=2y的焦点为F，准线为l，过l上一点P作抛物线的两条切线，切点分别为A、B。某学习小组在研究讨论中提出如下三个猜想：
⑴直线PA、PB恒垂直；⑵直线AB恒过定点F；⑶等式·=λ2中λ恒为常数。
现请你一一进行论证。
22．设函数f(x)与数列{an}满足下列关系：（14′）
①a1＞a，其中a是方程f(x)=x的实数根；②an＋1=f(an)(n∈N＋)
③f(x)的导函数f′(x)∈（0，1）；
⑴证明：an＞a；(n∈N＋)；⑵判断an与an＋1的大小，并证明你的结论。