高三数学备考解答题训练
概率与应用
班级__________ 姓名___________ 考号__________
高考方向：
概率可能作为应用题出现，但也有可能除概率外再有一道有关数列或函数不等式的应用题
概率部分强调：分清模型、规范格式
基本模型：等可能性事件、互斥事件(分类)、对立事件、独立事件同时发生、重复独立试验
1．热身题：
（1）某类电灯泡使用时数在1000小时以上的概率为0.2，则三个灯泡在使用1000小时以后最多只有一个坏的概率是_____________. （0.104）
所用模型：
（2）发报台分别以概率0.6和0.4发出信号“·”和“—”，由于通讯受到干扰，当发出信号“·”时，收报台未必收到信号“·”，而是分别以概率0.8和0.2收到信号“·”和“—”，同样，当发出信号“—”时，收报台分别以概率0.9和0.1收到信号“—”和“·”，
（I）收报台收到信号“·”的概率是_____________；（0.52）
（II）当收报台收到信号“·”时，发报台是发出信号“·”的概率是__________. (12/13)
所用模型：
（3）甲、乙二人各有一个装有3张卡片的盒子，从中取卡片来比胜负，甲的盒子中卡片的号码是2张1，1张3；乙的盒子中卡片的号码是1张1，2张2，甲乙两人同时从自己的盒子中取出1张比较，取出的不再放回，直到二人取的卡片号码不相同时，号码大的一方为胜，则甲获胜的概率是____________.（4/9）
所用模型：
（4）一学生在上学途中要经过6个路口，假设他在各个路口遇到红灯这一事件是相互独立的，并且概率都是
.
（I）他通过第3个路口时，首次遇到红灯的概率是_________；(4/27)
（II）他在途中恰好遇到3次红灯的概率是__________.(160/729)
（III）他在途中遇到红灯数ξ的期望是_________，方差是____________. (2，4/3)
所用模型：
| 窗口 | 1 | 2 | 过道 | 3 | 4 | 5 | 窗口 |
| 6 | 7 | 8 | 9 | 10 | |||
| 11 | 12 | 13 | 14 | 15 | |||
| 16 | 17 | … | … | … |
（5）两游客坐火车旅游，希望座位是连在一起，且有一个靠窗，已知火车上的座位的排法如图，则下列座位号码符合要求的是
A）48,49 B）62,63 C）75,76 D) 84,85
| 型号 | 小包装 | 大包装 |
| 重量 | 100克 | 300克 |
| 包装费 | 0.5元 | 0.7元 |
| 售价 | 3.00元 | 8.40元 |
（6）已知每生产100克洗衣粉的原料和加工费为1.8元，某洗衣粉厂采用两种包装，其包装费及售价如右表所示，则下列说法中：
①买小包装实惠；②卖小包装盈利多；③买大包装实惠；
④卖1包大包装比卖3包小包装还要多盈利
所有正确的说法是
A）①② B）②③ C）③ D）③④
（7）把一边长为a的木制正方体模型旋成一个尽可能大的球模型，则旋去部分的体积为________.
（9）某饭店有n间客房，客房的定价将影响住房率，每天客房的定价与每天的住房率的关系如下表：
| 每间客房的定价 | 每天的住房率 |
| 90元 | 65% |
| 80元 | 75% |
| 70元 | 85% |
| 60元 | 90% |
要使此饭店每天收入最高，则每间房价应定为B
A．90元 B．80元 C．70元 D．60元
（8）一张厚度为0.1mm的巨大的矩形纸，每次将纸沿对边中点连线剪开一起叠放，一共这样剪叠20次后所有纸的总厚度h1与一座塔的高度h2＝100m的大小关系为h1__________h2．
答以下解答题时，一定要注重格式
2．有两批产品，第一批20件，有5件一级品；第二批有12件，有2件一级品，今按两种抽样方法抽样：
（1）将两批产品混在一起，从中任取2件，求所抽两件均是一级品的概率；(21/496)
（2）从第一批中任取2件混入第二批中，再从混合后的第二批中抽取2件，试求所抽两件均是一级品的概率.(3/133)
3．某公司“咨询热线”电话共有10路外线，经长期统计发现，在8点至10点这段时间内，外线电话同时打入情况如下表所示：
| 电话同时打入数ξ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 概率P | 0.13 | 0.35 | 0.27 | 0.14 | 0.08 | 0.02 | 0.01 | 0 | 0 | 0 | 0 |
(1) 若这段时间内，公司只安排了2位接线员.(一个接线员一次只能接一个电话)
（I）求至少一路电话不能一次接通的概率;
（II) 在一周五个工作日中，如果有三个工作日的这一时间内至少一路电话不能一次接通，那么公司的形象将受到损害，现用至少一路电话不能一次接通的概率表示公司形象的“损害度”，求这种情况下公司形象的“损害度”；
(2) 求一周五个工作日的这一时间内，电话同时打入数ξ的期望.
4．某厂生产的A产品按每盒10件进行包装，每盒产品均需检验合格后方可出厂．质检办法规定：从每盒10件A产品中任抽4件进行检验，若次品数不超过1件，就认为该盒产品合格；否则，就认为该盒产品不合格．已知某盒A产品中有2件次品．
（1）求该盒产品被检验合格的概率；
（2）若对该盒产品分别进行两次检验，求两次检验得出的结果不一致的概率．
5．甲乙两人独立解某一道数学题，已知该题被甲独立解出的概率为0.6，被甲或乙解出的概率为0.92.
（1）求该题被乙独立解出的概率；
（2）求解出该题的人数
的数学期望和方差.
6．长江三峡大江截流工程有关数据如下表所示：
| 时 间 | 9:00 | 10:00 | 12:00 | … | 16:00 |
| 龙口宽 | 40m | 39m | 34m | … | |
| 工程进展 | 1m | 5m | … | ||
| 模拟数列 | a1 | a2+a3 | … | a7 |
预计16:00合龙.
(1)同学甲将工程进展情况模拟成等差数列，即a1=1,a2+a3=5,根据表中所列数据，通过计算，说明能否按期合龙.
(2)同学乙将工程进展情况模拟成等比数列，根据表中所列数据，通过计算，说明能否合龙(取
=4.6).
7．某工厂最近用50万元购买一台德国仿型铣床，在买回来以后的第二天投入使用，使用后的第t天应付的保养费是(t + 500)元，(买来当天的保养维修费以t = 0计算)，机器从买来当天到报废共付的保养维修费与购买机器费用的和平均摊到每一天的费用叫做每天的平均损耗．当平均损耗达到最小值时，机器报废最划算．
(1) 求每天平均损耗y (元)表示为天数x的函数；
(2) 求该机器买回来后多少天应报废．
8．为合理用电缓解电力紧张，某市将试行“峰谷电价”计费方法，在高峰用电时段，即居民户每日8时至22时，电价每千瓦时为0.56元，其余时段电价每千瓦时为0.28元．而目前没有实行“峰谷电价”的居民户电价为每千瓦时0.53元．若总用电量为S千瓦时，设高峰时段用电量为X千瓦时．
（1）写出实行峰谷电价的电费y1＝g1（x）及现行电价的电费y2＝g2（S）的函数解析式及电费总差额f(x)＝y2－y1的解析式；
（2）对于用电量按时均等的电器（在任何相同的时间内，用电量相同），采用峰谷电价的计费方法后是否能省钱?
（3）若每户实行“峰谷电价”的居民需缴纳安装“分时段电能计量表”的成本费100元．在用电量按时均等的条件下，一户居民要在一年内收回安装“分时段电能计量表”的成本费，每户每月用电至少要不低于多少千瓦时（结果取整数）?
9．某工厂有旧墙一面长14米，现准备利用这面旧墙建造平面图形为矩形，面积为126米2的厂房，工程条件是：①建1米新墙的费用为a元；②修1米旧墙的费用是a/4元；③拆去1米旧墙用所得的材料建1米新墙的费用为a/2元. 经过讨论有两种方案：
（1） 利用旧墙的一段x米(x<14)为矩形厂房的一面边长；
（2） 矩形厂房的一面边长x≥14.
问如何利用旧墙，即x为多少时建墙费用最省？（1）（2）两种方案哪种方案最好？
概率与应用题部分参考答案
3．（1）（I）解一. 只安排2位接线员，则3路及以上电话同时打入会至少有一路不能接通，
其概率P = 0.14 + 0.08 + 0.02 + 0.01 = 0.25 = 
.
解二. 只安排2位接线员，则2路及以下电话同时打入均能接通，
其概率P1 = 0.13 + 0.35 + 0.27 = 0.75 = 
，所求概率P = 1 – 
= 
. --- 4分
(II) “损害度”P = 
()3()2 = 
.
---
8分
(2) ∵在一天的这一时间内同时电话开入数ξ的期望为
0´0.13 + 1´0.35 + 2 ´ 0.27 + 3 ´ 0.14 + 4´ 0.08 + 5 ´ 0.02 + 6 ´ 0.01 = 1.79. --- 11分
∴ 一周五个工作日的这一时间电话打入数的期望等于 5 ´ 1.79 = 8.95 -- 12分
答略.
4．解: (1)从该盒10件产品中任抽4件，有等可能的结果数为
种，……………………1＇
其中次品数不超过1件有
种，…………………………………………………2＇
被检验认为是合格的概率为
……………4＇（本步正确，对上两步不作要求）
=……………………………………………………6＇
(2)两次检验是相互独立的，可视为独立重复试验，…………………………………………7＇
因两次检验得出该盒产品合格的概率均为，
故“两次检验得出的结果不一致”即两次检验中恰有一次是合格的概率为
…………………………………10＇
=…………………………………………11＇
答：该盒产品被检验认为是合格的概率为；两次检验得出的结果不一致的概率为…………12＇
说明：两小题中没有简要的分析过程，各扣1分．
5．解：（1）记甲、乙分别解出此题的事件记为A、B.
设甲独立解出此题的概率为P1，乙为P2. （2分）
则P（A）=P1=0.6, P(B)=P2
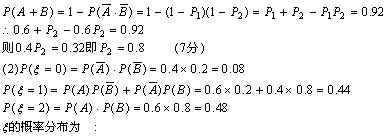
| ξ | 0 | 1 | 2 |
| P | 0.08 | 0.44 | 0.48 |
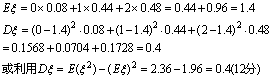
7．解：（1）第一天应付维修保养费a1 = 500元；
第二天应付维修保养费a2 = (500 + 1) 元；
第三天应付维修保养费a3 =（500 + 2）元；
┄
第x天应付维修保养费ax = [500 + (x－1)] 元. 2分
由此可知 {a n} 是首项a1 = 500，公差d = 1的等差数列，
∴ 前x天共付维修保养费Sx = a1x + d = 500x + , 4分
因而，每天平均费用y与时间x (天数)的函数关系为
y = (x Î N*) ,
即y = + + (x Î N*) . 7分
(2) 即y = + + ≥2 + = 1000 + = ,
当且仅当= ，即x = 1000时取等号， 11分
∴ x = 1000天时，机器报废最合算。 12分
8．解（1）若总用电量为S千瓦时，设高峰时段用电量为x千瓦时，则低谷时段用电量为
千瓦时
……………………………………………………………2分
…………………………………………………………………………………………………3分
电费总差额
………………………………………………4分
（2）可以省钱
令
，即
…………………………………………………………6分
对于用电量按时均等的电器而言，高峰用电时段的时间与总时间的比为：
能保证，即
所以用电量按时均等的电器采用峰谷电价的计算方法后能省钱．……………………………………9分
（3）由（Ⅱ）知，根据按时均等用电可知：
，即
令
，即
…………………………………………12分
得
答：每月用电量至少要不低于97千瓦时，才能在一年内收回成本． ………………………………14分
9．提示：
(1)(x<14)总费用y=
当且仅当a=12时ymin=35a.
(2)(x≥14)y=7a/2+2(x+126/x–7)a,由单调性x=14时ymin=35.5a,故第(1)方案最省.