高三数学练习题
一、选择题：
1．已知
和
是方程
的两根，则p、q间的关系是
（ D ）
A．
B．
C．
D．
2．如果数列
的前n项和
，那么这个数列
（ 
）
A．是等差数列而不是等比数列 B．是等比数列而不是等差数列
C．既是等差数列又是等比数列 D．既不是等差数列又不是等比数列
3．锐二面角
的棱l上一点A，射线
，且与棱成45°角，又AB与
成30°角，则二
面角的大小是
（ ）
A．30° B．45° C．60° D．90°
4．有6个人分别来自3个不同的国家，每一个国家2人。他们排成一行，要求同一国家的人不能相邻，那么他们不同的排法有 （ D ）
A．720 B．432 C．360 D．240
5．将
的图象向右平移
个单位，再作关于x轴的对称变换，得到函数
的图象，则
可以是
（ A ）
A．
B．
C．
D．
6．如果
，那么
的取值范围是 （ 
）
A．
，
B．，
C．，
， D．，
，
7．若圆
上有且仅有两个点到直线
的距离为1，则半径r的取值范围是
（ A ）
A．（4，6） B．[4，
C．（4，
D．[4，6]
8．某种体育彩票抽奖规定，从01到36共36个号码中抽出7个为一注，每注2元，某人想从01到10中选3个连续号，从11到20中选2个连续号，从21到30中选1个号，从31到36中选1个号组成一注，现这人把这些特殊的号全买，要花费的钱数是 （ D ）
A．3 360元 B．6 720元 C．4 320元 D．8 640元
9．已知ab≠0，
（x＞0，且x≠1），则
展开式中的常数项为
（ ）
A．12 B．60 C．30 D．160
10．已知O是
内一点且满足
，试问O点是的 （ ）
A 重心 B 垂心 C 外心 D 内心
二、填空题：
11．已知△ABC中，
，
，且
是方程
的两根，
，则AB的长为 
。
12．若函数
的图象关于直线
对称，则实数
。
13．空间有四个不同的平面，则这四个平面可能形成的交线条数取值的集合是
。
14．已知
是直线
上的动点，
是圆
的两切线，
为切点，
为圆心，那么四边形
的面积最小时点坐标为 
。
15．已知P是以
、
为焦点的双曲线
上一点，
⊥
，且
，则此双曲线的焦距与实轴长的比值为
．
16．当
时，
的大小关系是 
。
三、解答题：
17．在△ABC中，已知角A、B、C所对的三边a，b，c成等比数列．
（1）求证：
；（2）求函数
的值域．
解：（1）∵a、b、c成等比数列，∴
，由余弦定理得：
又∵∠B
（0，
），∴0＜∠B≤
．
（2）
，∵0＜∠B≤，
∴
，∴
，即原函数的值域是（1，
18．设
（1）如果当
时，恒有
，求
的值；
（2）
且
若的最大值为0,求
的值。
解：（1）∵，∴
，即
，得
（2）
∵
，由
， 得 
再由 
，得 
。
19．已知等比数列及等差数列
，其中
，公差d≠0．将这两个数列的对应项相加，得一新数列1，1，2，…，试求这个新数列的前10项之和．
解：的公比为q，由题知：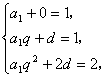
解得
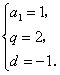则
，
．
这个新数列的前10项之和为
20．如图，△ABC中，AC＝BC，AE和CD都垂直于平面ABC，且AE＝AB＝2，F为BE的中点，
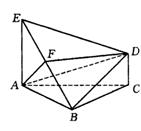DF∥平面ABC，
（1）求CD的长；
解：取AB中点G，连FG、CG，则FG∥AE，又AE和CD都垂直于
平面ABC，∴AE∥CD，∴FG∥CD，∴F、G、C、D四点共面．
又平面
平面ABC＝CG，DF∥平面ABC，∴DF∥CG，
∴四边形FGCD是平行四边形，∴
．
（2）求证：AF⊥BD；
解：直角三角形ABE中，AE＝AB，F是BE的中点，∴AF⊥BE，又△ABC中，AC＝BC，G是AB中点，∴CG⊥AB，又AE垂直于平面ABC，∴AE⊥CG，又
，∴CG⊥面ABE．
∵DF∥CG，∴DF⊥面ABE，∴AF⊥DF，又∵
，∴AF⊥面BED，∴AF⊥BD．
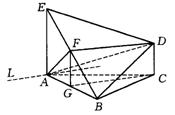（3）求平面ADF与平面ABC所成的二面角的大小．
解：设面
面ABC＝L，∵DF∥平面ABC，
∴DF∥L，又DF⊥面ABE，∴L⊥面ABE，
∴L⊥AF，L⊥AB，∴∠FAB即为二面角的平面角．
直角三角形ABE中，易得∠FAB＝45°，
∴平面ADF与平面ABC所形成的较小的二面角为45°
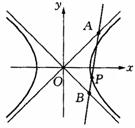21．如图，P为双曲线（a、b为正常数）上任一点，过P点作直线分别与双曲线的两渐近线相交于A、B两点．若
．
（1）求证：A、B两点的横坐标之积为常数；
（2）求△AOB的面积（其中O为原点）．
解：（1）设A（
，
）、B（
，
）、P（
，
）．∵
，
∴
，
．又
，
．∴
．
从而
．又∵P点在双曲线上．∴
，
为常数．
（2）又∠
，则
，
，
22．对于函数
（a＞0），如果方程
有相异两根，．
（1）若
，且的图象关于直线x＝m对称．求证：
；
（2）若
且
，求b的取值范围；
（3）
、为区间
，
上的两个不同的点，求证：
．
解：（1）
，且a＞0．∵，所以
，
即
，于是
．
（2）由方程
，可知
，∴、同号．
由，则
，∴
，∴
，即4a＋2b-1＜0 ①
又
，∴
，（∵a＞0）代入①式得：
，解之得
．
（3）由条件得
，
，不妨设
，
则
故
．