高三数学模拟试题（理）
本试卷分第I卷（选择题）和第II卷（非选择题）两部分，满分150分，用时120分钟）.
参考公式：
如果事件A、B互斥，那么P（A+B）＝P（A）+P（B）
如果事件A、B相互独立，那么P（AB）＝P（A）P（B）
如果事件A在一次试验中发生的概率是P，
那么n次独立重复试验中恰好发生k次的概率
．
球的表面积公式S＝4πR2，其中R表示球的半径
球的体积公式
，其中R表示球的半径
第Ⅰ卷（选择题，共60分）
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的4个选顶中，只有一项是符合题目要求
的.
1、复数
的模为
，则实数a 的值是（ ）
A．
B．3
C．
D．±3
2、在等比数列{an}中，an>0 ，且a2＝1-a1 ，a4＝9-a3 ，则a4+a5 ＝（ ）
A．16 B．27
C．36 D．81
3、使得点A（cos2α，sin2α）到点B（cosα，sinα）的距离为1的α 的一个值是（ ）
A．
B．
C．
D．
4、已知偶函数f(x)＝logax+b在（0，+∞）上单调递减，则f(b-2) 与f(a+1)的大小关系是（ ）
A．f(b-2)<f(a+1) B．f(b-2)＝f(a+1)
C．f(b-2)>f(a+1) D．无法确定的
5、设一个正多面体的面数为F，顶点数为V，若F+V＝8，且它的各条棱长都等于4，则这一多面体的外接球的球面
面积是（ ）
A．12π B．24π
C． 16π D．28π
6、曲线C与曲线y＝2x-3 图象关于直线l:y＝x 对称，则曲线C与l 的有一个交点位于区间（ ）
A．(-2，-1) B．（2，3）
C．（1，2） D．（-1，0 ）
7、已知双曲线kx2-y2＝1 的一条渐近线与直线2x+y+1＝0 垂直，则这一双曲线的离心率是（ ）
A．
B．
C． D．
8、一个盒子里装有相同大小的黑球10个，红球12个，白球4个，从中任取2个，其中白球的个数记为ξ ，则下列
算式中等于
的是（ ）
A．P(0<ξ≤2) B．P(ξ≤ 1)
C．Eξ D．Dξ
9、若
且
，则
（ ）
A．256 B．136
C．120 D．16
10、已知椭圆有这样的光学性质：从椭圆的一个焦点出发的光线，经椭圆反射后，反射光线必经过椭圆的另一个
焦点.今有一个水平放置的椭圆形台球盘，点A、B是它的两个焦点，长轴长为2a，焦距为2c.当静放在点A的
小球（小球的半径不计），从点A沿直线击出，经椭圆壁反弹后再回到点A，小球经过的路程是（ ）
A．4a B．2(a-c)
C．2(a+c) D．以上种情况都有可能
11、已知不等式logx(2x2+1)<logx(3x)<0 成立，则实数x 的取值范围是（ ）
A．（0，
） B．（0，
）
C．（，1） D．（，）
12、已知一个半径为
的球中有一个各条棱长都相等的内接正三棱柱，则这一正三棱柱的体积是（ ）
A．
B．
C．
D．
第Ⅱ卷（非选择题，共90分）
二、填空题：本大题共4小题，每小题4分，共16分．把各题的结果直接填在各题中的横线上．
13、函数
的图象中相邻两条对称轴的距离是___________.
14、给出下列三对函数：①
；②
；
③
；
其中有且仅有一对函数“既互为反函数，又同是各自定义域上的递增函数”，则这样的两个函数的导函数分别是f′(x)＝_________，g′(x)_________.
15、在ΔABC中，BC＝1，
，当ΔABC的面积等于时，tanC＝________．
16、已知抛物线y2＝2px(p>0) 的焦点在直线 y＝x-2上，现将抛物线沿向量a进行平移，且使得抛物线的焦点沿
直线y＝x-2 移到点（2a，4a+2 ）处，则平移后所得抛物线被y轴截得的弦长
＝ _________.
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
17、（本小题满分12分）设O为坐标原点，已知向量
分别对应复数 z1、z2，且
（其中a∈R），若
可以与任意实数比较大
小，求的值.
18、（本小题满分12分）已知函数
，其中
.
（1）判断函数的增减性；
（2）若命题
为真命题，求实数x 的取值范围.
19、（本小题满分12分）如图所示，已知四边形ABCD、EADM和MDCF都是边长为a的正方形，点P、Q分别是ED和
AC的中点，求：
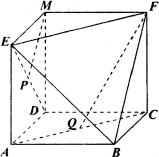
（1）
与
所成的角；
（2）P点到平面EFB的距离；
（3）异面直线PM与FQ的距离.
20、（本小题满分12分）某市出租车的起步价为6元，行驶路程不超过3km时，租车费为6元，若行驶路程超过
3km，则按每超出1km（不足1km也按1km计程）收费3元计费.设出租车一天行驶的路程数ξ（按整km数计
算，不足1km的自动计为1km）是一个随机变量，则其收费数η
也是一个随机变量.已知一个司机在某个
月中每次出车都超过了3km，且一天的总路程数可能的取值是200、220、240、260、280、300（km），它
们出现的概率依次是0.12、0.18、0.20、0.20、100a2+3a、4a .
（1）求作这一个月中一天行驶路程ξ的分布列，并求ξ的数学期望和方差；
（2）求这一个月中一天所收租车费η的数学期望和方差.
21、（本小题满分12分）已知函数
具有下列性质：
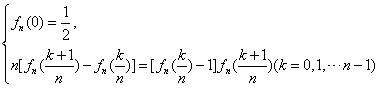
（1）当 n一定，记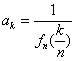
，求 ak的表达式（k＝0，1，…，n ）；
（2）对
，证明
.
22、（本小题满分14分）已知椭圆E：
，以F1（ -c，0）为圆心，以a-c 为半径作圆
F1，过点B2（0，b ）作圆F1的两条切线，设切点为M、N.
（1）若过两个切点M、N的直线恰好经过点B1（0，-b ）时，求此椭圆的离心率；
（2）若直线MN的斜率为-1 ，且原点到直线MN的距离为
，求此时的椭圆方程；
（3）是否存在椭圆E，使得直线MN的斜率k 在区间
内取值？若存在，求出椭圆E的离心率e
的取值范围；若不存在，请说明理由.
答案：一、1、C 提示：解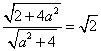
得.
2、B 提示：即
.
3、C
提示： 
.
4、A 提示：必有b＝0，且0<a<1，f(b-2)＝f(2)，而2>a+1>0.
5、B 提示：即求棱长为4的正四面体的外接球面积.
6、B 提示：由于函数是单调函数，∴ 这样的交点必在l:y＝x上，
令x＝2x-3，作y＝2x和y＝x+3的图象分析得有一个交点在区间(2，3)， 另一个交点在(-3，-2)区间.
7、A 提示：渐近线方程是kx2-y2＝0，由此得
，再求a、c.
8、B 提示：作出概率分布可得.
9、A 提示：n＝4，在展开式中令x＝-1得
.
10、D 提示： 击出后第一次触壁可以是近焦点的一长轴端点，也可以是远焦点的一长轴端点，还可以是异于端点的一个点，三种情况下分别为2(a-c)、2(a+c)和4a
11、D 提示：必有0<x<1，且2x2+1>3x>1.
12、A 提示：
.
二、13、
提示：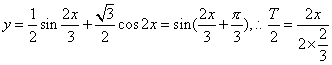
14、
提示：③中两个函数适合，利用指数函数和对数函数的求导法则可得.
15、
提示：由面积公式
得c＝4，由余弦定理得
.
16、
提示：由4a＋2＝2a－2，得a＝－2，∴平移后抛物线的焦点为F（－4，－6），
又
在y＝x－2上，∴p＝4，由此可求得平移公式为
，
代入原方程得平移后的抛物线方程是
，
令x＝0，得
三、17、解：依题意为实数，由
的虚部为0，
，解得a＝－5，或a＝3，又分母不为零，∴a＝3，
此时
，即
.
18、解：
(1)∵a∈｛a20<12a-a2｝，∴a2-12a+20<0，即2<a<10，∴函数y＝logax是增函数；
(2)
，
必有x>0，当0<x<
时，
，
不等式化为 
，
故
，
，
不等式化为
，
这显然成立，此时
；
当
时，
，不等式化为
，
；
综上所述知，使命题p为真命题的x的取值范围是
.
19、解：
建立空间直角坐标系，使得D(0，0，0)，A(a，0，0)，B(a，a，0)，C(0，a，0)，M(0，0，a)，E(a，0，a)，F(0，a，a)，则由中点坐标公式得
，
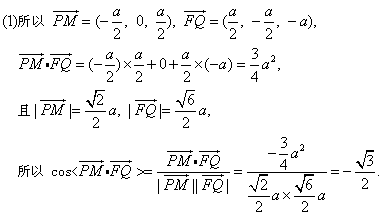
故得两向量所成的角为150°；
(2)设n＝(x，y，z)是平面EFB的单位法向量，即n＝1，n⊥平面EFB，
所以n⊥
，且n⊥
，又＝(－a，a，0)，
＝(0，a， －a)．
即有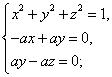
得其中的一个解是
，
．
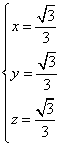设所求距离为d，则
.
(3)设e＝(x1，y1，z1)是两异面直线的公垂线上的单位方向向量，
则由
得
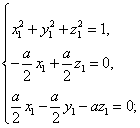求得其中的一个
，
而
，设所求距离为m，则
20、解：
(1)由概率分布的性质2有，0.12+0.18+0.20+0.20+100a2+3a+4a＝1，
∴100a2+7a＝0.3，∴ 1000a2+70a-3＝0，
，
或
(舍去)，即a＝0.03，
∴100a2+3a＝0.18，4a＝0.12，∴ξ的分布列为
∴Eξ＝200×0.12+220×0.18+240×0.20+260×0.20+280×0.18+300×0.12＝250(km)
Dξ＝502×0.12+302×0.18+102×0.20+102×0.20+302×0.18+502×0.12＝964;
(2)由已知η＝3ξ-3(ξ>3，ξ∈Z），∴ Eη＝E(3ξ-3)＝3Eξ-3＝3×250-3＝747(元)，
Dη＝D(3ξ-3)＝32Dξ＝8676.
21、解：
（1）
，
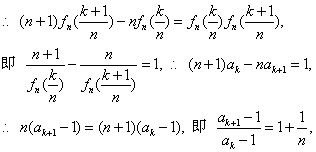
由n为定值，则数列
是以
为首项，
为公比的等比数列，
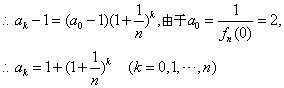
（2）
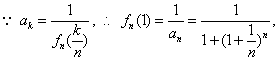
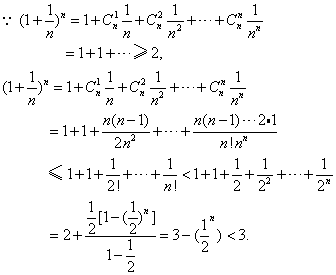
22、解：
(1)圆F1的方程是(x+c)2+y2＝(a-c)2，
因为B2M、B2N与该圆切于M、N点，所以B2、M、F1、N四点共圆，
且B2F1为直径，则过此四点的圆的方程是
，
从而两个圆的公共弦MN的方程为
cx+by+c2＝(a-c)2，又点B1在MN上，∴a2+b2-2ac＝0；∵b2＝a2-c2，
∴2a2-2ac-c2＝0，即e2+2e-2＝0，∴
(负值舍去)；
(2)由(1)，MN的方程为cx+by+c2＝(a-c)2，由已知
，∴b＝c，
而原点到MN的距离
，
∴a＝4，b2＝c2＝8，所求椭圆方程是
；
(3)假设这样的椭圆存在，由(2)则有
.
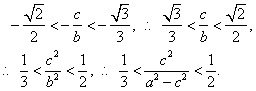故得
求得
，
即当离心率取值范围是
时，
直线MN的斜率可以在区间内取值.