高三数学模拟试题(文)
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,用时120分钟.
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(AB)=P(A)P(B)
如果事件A在一次试验中发生的概率是P,
那么n次独立重复试验中恰好发生k次的概率![]()
球的表面积公式S=4πR2,其中R表示球的半径
球的体积公式![]() ,其中R表示球的半径
,其中R表示球的半径
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的4个选顶中,只有一项是符合题目要求的.
1、已知向量![]() 的模为
的模为![]() ,则实数a的值是( )
,则实数a的值是( )
A.-1 B.2
C.-1 或2 D.1或-2
2、在等比数列{an}中,an>0 ,且a2=1-a1 ,a4=9-a3 ,则a4+a5 =( )
A.16 B.27
C.36 D.81
3、使得点A(cos2α,sin2α)到点B(cosα,sinα)的距离为1的α 的一个值是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4、已知偶函数f(x)=logax+b在(0,+∞)上单调递减,则f(b-2) 与f(a+1)的大小关系是( )
A.f(b-2)<f(a+1) B.f(b-2)=f(a+1)
C.f(b-2)>f(a+1) D.无法确定的
5、将一块边长为2的正三角形铁皮沿各边的中位线折叠成一个正四面体,则这一正四面体某顶点到其相对面的距
离是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6、已知点A(m-1,m+1)与点B(m,m)关于直线l对称,则直线l的方程是( )
A.x+y-1=0 B.x-y+1=0
C.x+y+1=0 D.x-y-1=0
7、已知双曲线kx2-y2=1 的一条渐近线与直线2x+y+1=0 垂直,则这一双曲线的离心率是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8、如图,某电路中,在A、B之间有1,2,3,4四个焊接点,若焊接点脱落,则电路不通.则可能出现的使A、B之
间的电路不通的焊接点脱落的不同情况有( )

A.4种 B.10种
C.12种 D.13种
9、设(3-x)n=a0+a1x+a2x2+…+anxn,若n=4 ,则 a0-a1+a2-… +(-1)nan=( )
A.256 B.136
C.120 D.16
10、椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线必经过椭圆的另一个焦
点.今有一个水平放置的椭圆形台球盘,点A、B是它的两个焦点,长轴长为2a,焦距为2c.当静放在点A的小
球(小球的半径不计),从点A沿直线l击出,经椭圆壁反弹后再回到点A,若l与椭圆长轴的夹角为锐角,
则小球经过的路程是( )
A.4b B.2(a-c)
C.2(a+c) D.4a
11、已知不等式-1<logx(3x)<0成立,则实数x 的取值范围是( )
A.(![]() ,1 ) B.(0,
,1 ) B.(0,![]() )
)
C.(![]() ,1) D.(
,1) D.(![]() ,
,![]() )
)
12、已知一个半径为![]() 的球中有一个各条棱长都相等的内接正三棱柱,则这一正三棱柱的体积是( )
的球中有一个各条棱长都相等的内接正三棱柱,则这一正三棱柱的体积是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把各题的结果直接填在各题中的横线上.
13、有一个简单的随机样本:6,10,12,9,14,15,则样本平均数![]() =__________.
=__________.
14、设棱锥的底面面积是8,那么这个棱锥的中截面(过棱锥高的中点且平行于底面的截面)的面积是
__________.
15、函数![]() 的图象中相邻两条对称轴的距离是__________.
的图象中相邻两条对称轴的距离是__________.
16、已知抛物线y2=2px(p>0) 的焦点在直线 y=x-2上,现将抛物线沿向量a进行平移,且使得抛物线的焦点沿
直线y=x-2 移到点(2a,4a+2 )处,则在平移中抛物线的顶点移动的距离d=__________.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17、(本小题满分12分)已知非钝角ΔABC中,∠B=60°,边AB的长减去BC的长等于AC边上的高,若sinC和
-sinA分别是方程![]() 的两个根,求实数m 和角A、C的值.
的两个根,求实数m 和角A、C的值.
18、(本小题满分12分)已知函数![]() 在y 轴上的截距为1,且在曲线上一点
在y 轴上的截距为1,且在曲线上一点![]()
处的切线斜率为![]() ,求这一切线方程,并求该函数的极大值和极小值.
,求这一切线方程,并求该函数的极大值和极小值.
19、(本小题满分12分)已知函数![]() ,其中
,其中![]() .
.
(1)判断函数![]() 的单调性;
的单调性;
(2)若命题![]() 为真命题,求实数x 的取值范围.
为真命题,求实数x 的取值范围.
20、(本小题满分12分)如图所示,已知四边形ABCD、EADM和MDCF都是边长为a的正方形,点P、Q分别是ED和
AC的中点,求:
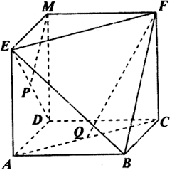
(1)异面直线PM与FQ所成的角;
(2)四面体P—EFB的体积;
(3)(附加题,满分5分,全卷总分不超过150分)异面直线PM与FQ的距离.
21、(本小题满分12分)已知等差数列{an} 的前四项的和为60,第二项与第四项的和为34,等比数列{bn}
的前四项的和为120,第二项与第四项的和为90.
(1)求数列 {an}、{bn} 的通项公式;
(2)对一切正整数n,是否存在正整数p,使得![]() ?无论存在与否,都请给出证明.
?无论存在与否,都请给出证明.
22、(本小题满分14分)有如下命题:已知椭圆![]() ,AA′是椭圆的长轴,P(x1,y1)是椭圆上异
,AA′是椭圆的长轴,P(x1,y1)是椭圆上异
于A、A′的任意一点,过P点斜率为![]() 的直线l ,若直线l上的两点M、M′在x轴上的射影分别为
的直线l ,若直线l上的两点M、M′在x轴上的射影分别为
A、A′,则
(1)AMA′M′为定值4;
(2)由A、A′、M′、M四点构成的四边形面积的最小值为12.
请分析上述命题,并根据上述问题对于椭圆
![]() (a>b>0)构造出一个具有一般性结论的命题.写出这一命题,并判断这一命题的真假.
(a>b>0)构造出一个具有一般性结论的命题.写出这一命题,并判断这一命题的真假.
答案:一、1、C 提示:解![]() 得.
得.
2、B 提示:即![]() .
.![]()
3、C 提示: ![]() .
.
4、A 提示:必有b=0,且0<a<1,f(b-2)=f(2),而2>a+1>0.
5、A 提示:即求棱长为1的正四面体的高, ∴为![]() .
.
6、B 提示:直线与AB垂直,且过AB的中点, 故得![]() =1,且过点
=1,且过点![]() .
.
7、A 提示:渐近线方程是kx2-y2=0,由此得![]() ,再求a、c.
,再求a、c.
8、D 提示:1号接点脱落,有23种情况;1号接点正常,2号脱落有22种情况;
1号、2号接点正常,3、4号接点都脱落有1种情况.
9、A 提示:在展开式中令x=-1得![]() .
.
10、D 提示:由椭圆的第一定义得4a.
11、D 提示:必有0<x<1,且 ![]() >3x>1.
>3x>1.
12、A 提示:![]() .
.
二、13、11 提示:即![]() .
.
14、2 提示: 设中截面面积是S,则![]() .
.
15、![]() 提示:
提示: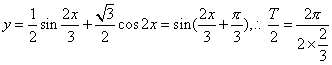 .
.
16、![]() 提示:由4a+2=2a-2,得a=-2, ∴平移后抛物线的焦点为F(-4,-6),
提示:由4a+2=2a-2,得a=-2, ∴平移后抛物线的焦点为F(-4,-6),
又(![]() ,0)在y=x-2上,∴p=4, 由此可以求得平移公式为
,0)在y=x-2上,∴p=4, 由此可以求得平移公式为![]() ,
,
代入原方程得平移后的抛物线方程是(y+6)2=8(x+6), 其顶点坐标为(-6,-6)) .
三、17、解:设△ABC的AC边上的高为h,由∠B=60°,且三角形是非钝角三角形,
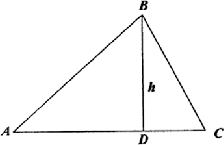
![]() ,依题意得AB-BC=h,
,依题意得AB-BC=h,
![]() ,故得sinC-sinA=sinCsinA,
,故得sinC-sinA=sinCsinA,
又sinC和-sinA是方程![]() 的两个根,
的两个根,
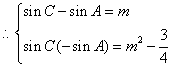 ;
;![]() ,即
,即![]() ,
,
![]() ,此时方程为
,此时方程为![]() ,
,
它的两个根是![]() 和x2=1,,∴ sinC=1,
和x2=1,,∴ sinC=1,
![]() ,即有A=30°,C=90°.
,即有A=30°,C=90°.
18、解:依题意,f(0)=1,∴b=1,又∵f′(x)=x2-a,由已知![]() ,
,
![]() ,
,![]() ,
,
∴所求的切线方程是 ![]()
令![]() ,
,
∵当![]() 时,f′(x)>0,当
时,f′(x)>0,当![]() ,
,
当![]() ,∴
函数f(x)有极大值
,∴
函数f(x)有极大值![]() ,
,
极小值![]() .
.
19、解:
(1)∵a∈{a20<12a-a2},∴a2-12a+20<0,
即2<a<10,∴函数y=logax是增函数;
(2)![]() ,必有x>0,当0<x<1,
,必有x>0,当0<x<1,
![]() ,不等式化为
,不等式化为![]() ,
,
这显然成立,此时0<x<1;
当![]() 时,
时,![]() ,不等式化为
,不等式化为![]() ,
,
![]() ,故
,故![]() ,此时
,此时![]() ;
;
综上所述知,使命题p为真命题的x的取值范围是![]() .
.
20、解:
(1)将已知图形以AD、DC、DM为相邻的三条棱补成如图所示的正方体,易知BF∥MP,
连结BQ,则∠QFB即为异面直线PM与FQ所成的角,
由正方体的性质知△BFQ是直角三角形,由![]() ,
,
知∠QFB=30°,即所求的角为30°;
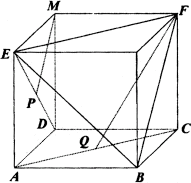
(2)由于DP=PE,所以四面体P-EBF的体积等于四面体D-EBF的一半,
所以所求的体积![]() .
.
(3)由(1)异面直线PM与FQ的距离即为MP到平面BFQ的距离,
也即M点到平面BFD的距离,设这一距离为d,
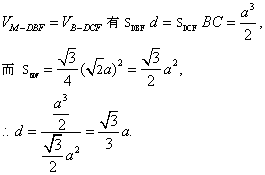
21、解:
(1)设等差数列的首项为a1,公差为d,
等比数列的首项为b1,公比为q,
依题意有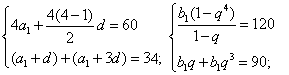
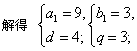 ∴ an=4n+5,bn=3n;
∴ an=4n+5,bn=3n;
(2)由(1)![]() 令4p+5=9n,得
令4p+5=9n,得![]() ,
,
而![]() ,
,
由于![]() ,∴ 9n-5≥4,且上式小括号中的数为8的倍数,
,∴ 9n-5≥4,且上式小括号中的数为8的倍数,
故对于一切正整数n,使得![]() 的正整数p总存在.
的正整数p总存在.
22、解:
这一命题是:已知![]() ,AA′是椭圆的长轴,P(x1,y1)是椭圆上异于A、A′的任意一点,过P点作斜率为
,AA′是椭圆的长轴,P(x1,y1)是椭圆上异于A、A′的任意一点,过P点作斜率为![]() 的直线l,若直线l上的两点M、M′在x轴上的射影分别为A、A′,则(1)AMA′M′为定值b2;(2)由A、A′、M′、M四点构成的四边形面积的最小值为2ab.这一命题是真命题,证明如下:
的直线l,若直线l上的两点M、M′在x轴上的射影分别为A、A′,则(1)AMA′M′为定值b2;(2)由A、A′、M′、M四点构成的四边形面积的最小值为2ab.这一命题是真命题,证明如下:
(1)不妨设A(-a,0)、 A′(a,0),由点斜式得直线l的方程是![]() ,
,
即![]() ,由射影的概念知M与A、M′与A′有相同的横坐标,
,由射影的概念知M与A、M′与A′有相同的横坐标,
由此可得, ![]() ,
,
![]() ;
;
(2)由图形分析知,不论四点的位置如何,四边形的面积S=![]() AA′(AM+A′M′),
AA′(AM+A′M′),
∵AA′=2a,且AM、A′M′都为正数,
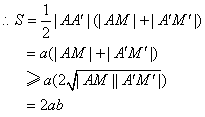
即四边形的面积的最小值为2ab.