高三专题突破—《平面向量》

高三专题突破—《平面向量》

　　　　　　　　　　　　　　　　  班级　　　　姓名　　　　　　

1、已知＝（4，3），向量是垂直于的单位向量，则_{＝　　　　　　　　  （　　 ）}

（A）（ ，－）或（－ ，）　  （B）（ ，－）或（－ ，）

（C）（ ，）或（－ ，－）　　（D）（ ，）或（ ，）

2、下列向量组中能作为表示它们所在平面内的所有向量的基底的是　　　　　  （　　 ）

A.e₁=（0，0），e₂=（1，－2）　　　　　B.e₁=（－1，2），e₂=（5，7）

C.e₁=（3，5），e₂=（6，10）　　　　　　D.e₁=（2，－3），e₂=（，－）

3、△ABC中，=，=，·<0，S_△ABC=，=3，=5，则、夹角

为（　　）　 (A)30　　　　(B) －150 　　 (C)150　 　(D) 30或150

4、平面直角坐标系中，O为坐标原点，已知两点A（3，1），B（－1，3），若点C满足=α+β,其中α、β∈R,且α+β=1,则点C的轨迹方程为　　　　　　　 （　　）

A.3x－2y－11=0　　　 B.（x－1）²+(y－2)²=5　　　C.2x－y=0　　 D.x+2y－5=0

5、将函数y=的图象F，按a=（，－1）平移到F′,则F′的解析式为（　　）

A.y=sin2x－1　　　　 B.y=cos2x+1　 C.y=sin(2x-)-1　　　　　　　D.y=cos(2x－)+1

6、将函数y=2x的图象按向量平移后得到函数y=2x+6的图象，给出以下四个命题：

①的坐标可以是（-3，0）②的坐标可以是（6，0）③的坐标可以是（-3，0）或（0，6）④的坐标可以有无数中情况。其中真命题的序号是　　　　　　　　　  ；

7、有下列四个命题：①＋＋＝0　②0 ·＝  ③（· ）·＝ ·（·）

④＋²＝(＋)²⑤若∥，则· ＝ · ⑥若⊥，则- ＝+　

⑦若，不共线，且=，则（+）（-）=0　 ⑧在平行四边形ABCD中

。其中真命题的序号是　　　　　　　　　　　　　　　　　

8、

9、设坐标原点为O，抛物线y²=2x与经过焦点的直线交于A、B，则=　　　　　　 

10、已知a=（,2）,b=(3,+1)且a与b的夹角是钝角，则实数λ的取值范围是_____________.

11、已知a=3，b=5，且a·b=12，则向量a在向量b的方向上的投影为_____________.

12、已知++=0，==，则，的夹角为_________.

13、点P在平面上按向量作匀速直线运动，当t=0时，点P在（-6，-2）处，则当t=6时点P的坐标为　　　　　　　　

14、已知A、B、C三点共线，O是该直线外的一点，设，，且存在实数m使成立，则点A分的比为　　　　　　　   ；

15、已知：D为△ABC的边BC上的中点，E是AD上的一点，且=3，若=a，则++=_____________.（用a表示）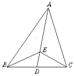

16、在水流速度为10km/h的河流中，要使船以km/h的速度与河岸成直角横渡，则船航行的速度为　　　　　　  , 与水流方向的夹角为　　　　　　  .

17、已知＝1，＝，①若∥，求 · ；②若、的夹角为60°，求＋。

18、如果4－2=（－2，2），=（1，），·=3，=4，求与夹角。