高中高三考前模拟试卷（二）
一、选择题（每小题5分，共60分）
1．已知集合A＝{0，2，4}，B＝{x｜x＝ab，a，
，a≠b}，则集合B的子集的个数为
A．4 B．8 C．16 D．15
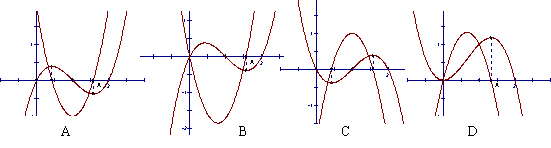2．以下四图，都是同一坐标系中三次函数及其导函数的图象，其中一定不正确的序号是
3．已知
和
是方程
的两根，则p、q间的关系是（ ）．
A．
B．
C．
D．
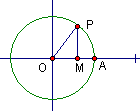4．质点P在半径为r的圆周上逆时针做匀速运动，角速度为1rd/s，设A为起点，那么在t时刻，点P在x轴上的射影点M的速度为：
A．rsint B．－rsint
C．rcost D．－rcost
5．直线ax－by－a＋1=0，被圆x2＋y2＋2y－24=0截得的弦的中点M的坐标为(－2,1)，则a＋b的值是：
A．2 B．1 C．3 D．
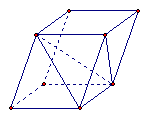
6．以平行六面体相邻两个面上互相异面的两条面对角线的端点为顶点的四面体的体积是平行六面体体积的：
A． B． C． D．
7．设M={平面内的点(a,b)}，N={f(x)f(x)=acos2x＋bsin2x} ，给出M到N的映射：
f：(a,b)
f(x)= acos2x＋bsin2x。则点(1,)的象f(x)的最小正周期为：
A．π B．2π C． D．
8．等差数列
的前n项和记为
，若
为一个确定的常数，则下列各数中也是常数的是
A．
B．
C．
D．
9．如果
，那么
的取值范围是
A．[－，] B．[－，1]
C．[－，）∪（，1] D．[－，)∪(，1]
10．过抛物线y2=ax(a＞0)的焦点F作一直线交抛物线于A、B两点，若线段AF、BF的长分别为m,n，则等于：
A． B． C．2a D．
11．某种体育彩票抽奖规定，从01到36共36个号码中抽出7个为一注，每注2元，某人想从01到10中选3个连续号，从11到20中选2个连续号，从21到30中选1个号，从31到36中选1个号组成一注，现这人把这些特殊的号全买，要花费的钱数是（ ）．
A．3360元 B．6720元 C．4320元 D．8640元
12．已知函数f(x)=－2x＋1，对于任意正数a，使得f(x1)－f(x2)＜a(x1,x2∈R)成立的一个充分不必要条件是：
A．x1－x2＜a B．x1－x2＜ C．x1－x2＜ D．x1－x2＞
二、填空题（每小题4分，共16分）
13．一容量为20的样本数据，其频率分布直方图如图所示：
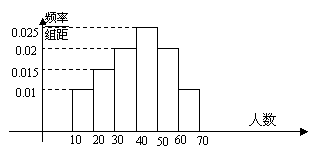则样本在(－∞,60]
上的频率为：
14．已知函数f(x)=x－22x2＋32x3－42x4＋……＋(－1)n－1n2xn(n∈N＋，n为常数)，
则f(1)= 。
15．已知过球面上A,B,C三点的截面和球心的距离是球直径的，且AB=5，AC⊥BC，则该球的表面积为__________．
16．对于函数
有以下四个结论：
①
的定义域为R； ②在（0，＋∞）上是增函数；
③是偶函数； ④若已知a，
，且
，则
．
其中正确的命题的序号是__________．
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题：
13 14 15 16
三、解答题（第17～21题每题12分，第22题14分，共74分）
17．已知等比数列及等差数列
，其中
，公差d≠0．将这两个数列的对应项相加，得一新数列1，1，2，…，试求这个新数列的前10项之和．
18．已知向量
，
，
，
，且
与
之间有关系式：
，其中k＞0．
（1）试用k表示
； （2）求的最小值，并求此时与的夹角
的值．
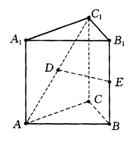
19．如图，在正三棱柱
中，各棱长都等于a，D、E分别是
、
的中点，
（1）求证：DE是异面直线与的公垂线段，并求其长度；
（2）求二面角
的大小；
（3）求点
到平面AEC的距离．
20．如图，P为双曲线
（a、b为正常数）上任一点，过P点作直线分别与双曲线的两渐近线相交于A、B两点．若
．
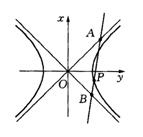（1）求证：A、B两点的横坐标之积为常数；
（2）求△AOB的面积（其中O为原点）．
21．某工厂去年的某产品的年产量为100万只，每只产品的销售价为10元，固定成本为8元．今年，工厂第一次投入100万元（科技成本），并计划以后每年比上一年多投入100万元（科技成本），预计产量年递增10万只，第n次投入后，每只产品的固定成本为
（k＞0，k为常数，
且n≥0），若产品销售价保持不变，第n次投入后的年利润为
万元．
（1）求k的值，并求出的表达式；
（2）问从今年算起第几年利润最高?最高利润为多少万元?
22．对于函数
（a＞0），如果方程
有相异两根
，
．
（1）若
，且的图象关于直线x＝m对称．求证：
；
（2）若
且
，求b的取值范围；
（3）、
为区间
，
上的两个不同的点，求证：
．
参考答案
1．A 2．C 3．D 4．B 5．D 6．C 7．A 8．B 9．B 10．A
11．D 12．B 13．
14．
15．
16．①②④
17．设的公比为q，由题知：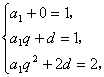
解得
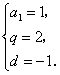则
，
．这个新数列的前10项之和为
18．（1）因为，所以
，
，
，
，
． （2）由（1）
，当且仅当
，即
时取等号．此时，
，
，
，所以的最小值为
，此时与的夹角
为
19．（1）取AC中点F，连接DF．因为D是的中点，所以DF∥
，且
．又
，E是的中点，所以DF∥BE，DF＝BE，所以四边形BEDF是平行四边形，所以DE∥BF，DE＝BF．因为⊥面ABC，
面ABC，所以⊥BF．又因为F是AC的中点，△ABC是正三角形，所以BF⊥AC，
．因为⊥BF，∥，所以BF⊥，所以BF⊥面
，又因为
面，所以BF⊥，因为DE∥BF，所以DE⊥，DE⊥，所以DE是异面直线与的公垂线段，且
． （2）因为，DE⊥，所以DE⊥，又因为DE⊥，所以DE⊥面．又
面
，所以面⊥面
，所以二面角的大小为90°． （3）连接CE，则三棱锥
的底面面积为
，高
．所以
．在三棱锥
中，底面△AEC中，
，则其高为a，所以
．设点到平面AEC的距离为d，由
得
，所以
，即点到平面AEC的距离为
20．（1）设A（，
）、B（，
）、P（
，
）．因为
，所以
，
．又
，
．所以
．从而
．又因为P点在双曲线上．所以
，
为常数． （2）又∠
，则
，
21．（1）由，当n＝0时，由题意，可得k＝8，所以
．
（2）由
．当且仅当
，即n＝8时取等号，所以第8年工厂的利润最高，最高为520万元
22．（1）
，且a＞0．因为，所以
，即
，于是
． （2）由方程
，可知
，所以、同号．由，则
，所以
，所以
，即4a＋2b-1＜0，又
，所以
，（因为a＞0）代入①式得：
，解之得
． （3）由条件得
，
，不妨设
，则
，故
．