高考冲刺模拟考试试卷数学试题

高考冲刺模拟考试试卷数学试题

第Ⅰ卷（选择题　共60分）

参考公式：

如果事件A、B互斥，那么　　　　　　　　　　　　　  球的表面积公式

P（A+B）=P（A）+P（B）　　　　　　　　　　　  S_球=4πR²

如果事件A、B相互独立，那么　　　　　　　　　　　  其中R表示球的半径

P（AB）=P（A）P（B）　　　　　　　　　　　  球的体积公式

如果事件A在一次试验中发生的概率是　　　　  　　　　

P，那么n次独立重复试验中恰好发生k次的概率　　　　 其中R表示球的半径

一、选择题：本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，有

且只有一项是符合题目要求的

1．若在　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．第一象限　　　　　　B．第二象限　　　　　　C．第三象限　　　　　　D．第四象限

2．已知集合等于　　　 （　　）

　　　 A．1　　　　　　　　　　　　B．2　　　　　　　　　　　　C．1或2　　　　　　　　 D．8

3．函数的定义域为　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　B．　　　　　　　 C．（1，2）　　　　　　　D．

4．设，则下列不等式成立的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　　　　　　　D．

5．某地区高中分三类，A类校共有学生4000人，B类校共有学生2000人，C类校共有学生

　 3000人，现欲抽样分析某次考试的情况，若抽取900份试卷进行分析，则从A类校抽取

　 的试卷份数应为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．450　　　　　　　　　　 B．400　　　　　　　　　　 C．300　　　　　　　　　　 D．200

6．如图，函数的图象如下，则函数的解析式为　　　　　　　　　　 （　　）

　　　 A．

　　　 B．

　　　 C．

　　　 D．

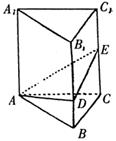
7．在底面边长为的正三棱柱ABC—A₁B₁C₁中，D、E分别为

　 侧棱BB₁、CC₁上的点且EC=BC=2BD，则截面ADE与底面

　 ABC所成的角为　　　　　　　　　　　　　　 （　　）

　　　 A．30°　　　　　　　　　 B．45°

　　　 C．60°　　　　　　　　　 D．75°

8．一旅社有100间相同的客房，经过一段时间的经营实践，发现每间客房每天的定价与住

　 房率有如下关系：

每间房定价	100元	90元	80元	60元
住房率	65%	75%	85%	95%

　 要使每天的收入最高，每间房定价应为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．100元　　　　　　　　B．90元　　　　　　　　　C．80元　　　　　　　　　D．60元

9．已知公差不为零的等差数列的第、、项依次构成等比数列的连续三项，则此等比

　 数列的公比q是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　B．　　　　　　　　C．　　　　　　　　D．

10．半径为1的球面上有三点A、B、C，A和B与A和C之间的球面距离都是，B和C

之间的球面距离是，则过A、B、C三点的截面到球心的距离是　　　　　　　　　 （　　）

A．　　　　　　　　　 B．　　　　　　　　　 C．　　　　　　　　 D．

11．已知函数，则必有　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　　　　　　　 D．

12．已知F₁和F₂是两个定点，点P是以F₁和F₂为公共焦点的椭圆和双曲线的一个交点，并

且分别是椭圆和双曲线的离心率，则有　　　　　　　　　　　　　　　（　　）

A．　　　 B．　　　 C．　　　　D．

第Ⅱ卷（非选择题，共90分）

二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中的横线上。

13．已知抛物线的焦点在直线上，若抛物线作如下移动，其

焦点沿直线滑动，对称轴作平行移动，那么当焦点移动到时，抛物线的

方程是　　　　　　　　　　　　　　　 .

14．已知，则方程可表示不同的

圆的个数是　　　　　　　　　　　　　　  .

15．设，且点B的坐标为B（3，－2，1）则点A的

坐标为　　　　　　　　　　　　　　　  .

16．定义一种运算“*”，对于正整数n满足以下运算性质：

　 （1）， （2）

则用含n的代数式表示是　　　　　　　　　　  .

三、解答题：本大题共6小题，满分74分，解答应写出文字说明、证明过程或演算步骤。

17．（本小题满分12分）

已知向量，求

①；

②（理科做）若的最小值是，求实数的值；

　（文科做）求函数的最小值.

18．（本小题满分12分）

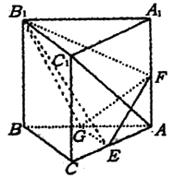
　　　　如图，在直三棱柱ABC—A₁B₁C₁中，AC=BC=AA₁=2，，E、F、G

分别是AC、AA₁、AB的中点.

①求异面直线AC₁与GF所成的角.

②求二面角B₁—EG—B的大小.

19．（本小题满分12分）

　　　　某工厂去年的某产品的年产量为100万只，每只产品的销售价为10元，固定成本

为8元. 今年，工厂第一次投入100万元（科技成本），并计划以后每年比上一年多投入

100万元（科技成本），预计产量年递增10万元，第n次投入后，每只产品的固定成本

为为常数，），若产品销售价保持不变，第n次

投入后的年利润为万元.

　 （1）求k的值，并求出的表达式；

　 （2）问从今年算起第几年利润最高？最高利润为多少万元？

20．（本小题满分12分）

（理）设函数是定义在上的奇函数，当时，

为实数）

①求：当的解析式；

②若在区间上为增函数，求a取值范围；

③求在区间上的最大值.

　 （文）已知，函数，

①当时，判断函数上单调性，并加以证明；

②求的取值范围，使上为增函数.

21．（本小题满分12分）

已知△OPQ的面积为S，且；

　 （1）若，求向量的夹角的取值范围；

　 （2）设以O为中心，P为焦点的椭圆经过点Q，当上变

动时，求的最小值，并求出此时的椭圆方程.

22．（本小题满分14分）

　　　　数列的前n项和为S_n，满足：，

　 （1）求证：数列是等比数列；

　 （2）设数列的公比为，数列满足的

通项公式；

　 （3）记

高考冲刺模拟考试训练题

数学参考答案

一、选择题（每小题5分，共计60分）

BCDCB　ABCAC　DD

二、填空题（每小题4分，共计16分）

13．　　14．24个　15．（－8，0，－22）　16．

三、解答题（本题共6小题，共计74分）

17．解：①a·b=

a+b=，

∵， ∴　∴ a+b=2cosx.

②（理科）　即

∵，　∴

时，当且仅当取得最小值－1，这与已知矛盾.

时，当且仅当取最小值

由已知得，解得

时，当且仅当取得最小值

由已知得，解得，这与相矛盾.

综上所述，为所求.

②（文科）

∵　 ∴，

∴当且仅当取得最小值

18．解：①连结A₁B、A₁C，由已知得A₁B//FG　∵BC⊥平面A₁ACC₁，且AC₁⊥A₁C，

∴A₁B在平面A₁ACC₁上的射影为A₁C.　由三垂线定理，得AC₁⊥A₁B，

∴FG⊥AC₁，即AC₁与GF所成的角为90°

②过点B作BT⊥EG交EG的延长线于T，连B₁T，　∵BB₁⊥平面ABC，

∴B₁T⊥EG，　∴∠B₁TB为二面角B₁—EG—B的平面角.

又∵GE//BC，AC⊥BC，　∴AC⊥GE， ∴AC//BT　∴ECBT为矩形，

∴BT=1，　在△BTB₁中，故二面角B₁—EG—B的大小为arctan2.

19．解：（1）由时，由题意可得k=8，

∴，

（2）由

=，

当且仅当，即n=8时，取等号.

∴第8年工厂的利润最高，最高为520万元.

20．解：（理）①设　又∵为奇函数，

∴　 ∴

②∵上为增函数，　

∴上恒成立，

∴上恒成立，　∴a>－1.

当a=－1时也成立，　∴

③（1）∵当时，上递增，　 ∴

（2）当a<－1时，由时，

∴内单调递减

∴

（文）解：①

∵，　∴，　 ∴

故当a=2时，函数为增函数.

②由题意得：

当时，恒成立，

又，故

21．解：（1）∵夹角为，∴与夹解为，

∴

又　 ∴

　∴　　∴

（2）以O为原点，所在直线为x轴建立直角坐标系，

∴

∴　∴，

由　∴

∴　∴

令上是增函数，

∴上为增函数，

∴当m=2时，

此时P（2，0），椭圆另一焦点为P′（－2，0），则椭圆长轴长

，

　故椭圆方程为

22．解：（1）　①，　　　②

②－①得：，∴

又　　解得：

∴，　　∴是等比数列.

（2）　∴

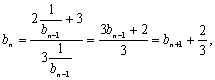
∴　∴数列为等差数列，

（3）

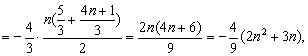
当为减函数，　 ∴