试卷类型：A
高考模拟考试（三）
数学试题（文）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.第Ⅰ卷1至2页，第Ⅱ卷3至8页.考试结束后，将本试卷和答题卡一并交回. 共150分，考试时间120分钟.
第Ⅰ卷（选择题 共60分）
注意事项：
1．答第Ⅰ卷前，考生必将自己的姓名、准考证号、考试科目、试卷类型（A）用铅笔涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，不能答在试题卷上。
参考公式:
三角函数的积化和差公式 正棱台、圆台的侧面及公式
其中
、
分别
表示上、下底面周长，
表示斜高或母线长
球的体积公式 
其中R表示
球的半径
一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.
(1)集合
，若
，
，则
，则运算
可能是
(A)加法 (B)减法 (C)乘法 (D)除法
(2)复数
、
，则
的充要条件是
(A)
(B)
(C)
(D)
(3)不等式
的解集为
，则函数
的图象为
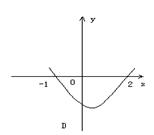
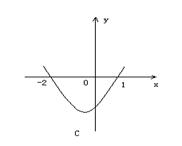
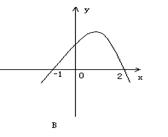
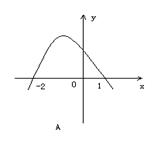
(4)已知
，则
(A)
(B)
(C)
(D)
(5)函数是定义在R上的偶函数，且最小值为2，则函数
是
(A)奇函数，最小值为
(B)偶函数，最大值为
(C)奇函数，最大值为
(D)偶函数，最小值为
(6)函数
，给出下列命题，其中正确的是
(A)当
时，
(B)函数
在区间
上是增函数
(C)函数的图象关于直线
对称
(D)函数的图象是由函数
的图象向左平移
个单位得到
(7)已知圆
与直线
和
轴都相切，则
=
(A)1
(B)2
(C)
(D)与
有关
(8)在正数
、
之间插入数
，使之成为等差数列，又、之间插入数、
使之成为等比数列，则有
(A)
(C)
(C)
(D)
(9)一个圆锥有三条母线两两垂直，则它的侧面展开图的圆心角为
(A)
(B)
(C)
(D)
(10)双曲线
与抛物线
交于
、
两点，若直线
既过双曲线的焦点，又过抛物线的焦点，则此双曲线的离心率为
(A)
(B)
(C)2
(D)3
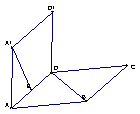(11)在直二面角
中，四边形
、
是长方形，已知
，
，
为
的中点，则异面直线
与
所成角的余弦值为
(A)
(B)
(C)
(D)
(12)某纯净水制造厂在净化水过程中，每增加一次过滤可减少水中杂质20%，要使水中杂质减少到原来的5%以下，则至少需过滤的次数为（参考数据lg2=0.3010,lg3=0.4771）
(A)5 (B)10 (C)14 (D)15
高考模拟考试（三）
数学试题（文）
第Ⅱ卷（非选择题 共90分）
注意事项：
1. 第Ⅱ卷共7页，用钢笔或圆珠笔直接答在试卷上.
2. 答卷前将密封线内的项目填写清楚.
二、填空题：本大题共4小题，每小题4分，共16分. 把答案填在题中的横线上.
(13)
的展开式中的常数项为__________________.
(14) 一山坡与水平面成
二面角，坡脚的水平线上有两点
、
，若甲沿山坡面自朝垂直于的方向向上走30米至
，乙沿水平面自朝垂直于的方向向前走30米至
，若
米，则此时甲、乙两人间的直线距离为约_______________（精确到
米）.
(15)对某种产品中的10件不同的正品和2件不同的次品，一一进行测试，到区分出所有次品为至，若所有次品中恰好在第四次测试中全部出现，则测试的方法有____________种.
(16)椭圆两焦点
、
，椭圆上满足
的点个数为______________.
三、解答题：本大题共6小题，共74分. 解答应写出文字说明，证明过程或演算步骤.
（17）（本小题满分12分）解不等式
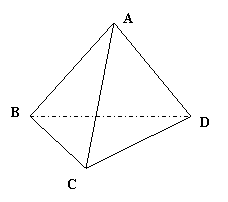（18）（本小题满分12分）如图，四面体中，
与
都是边长为4的正三角形
(I)求证：
(II)若点到平面
的距离不小于3，求二面角
的平面角的取值范围
(III)在②条件下，求四面体体积的最大值与最小值.
（19）（本小题满分12分）已知函数
的反函数
，
(I)若
，求
的取值范围
(II)设函数
，当
时，求
的值域
（20）（本小题满分12分）已知动点到定点
的距离比它到定直线
的距离小1
(I)求动点的轨迹方程
(II)设点是①中轨迹上任意一点，试问：是否存在常数
，使得在直线
上存在唯一点，满足
，若存在，求出常数，若不存在，请说明理由。
（21）（本小题满分12分）某人从A地乘出租车到B地，由两种方案. 第一种方案：租用起步价10元，每千米为1.2元的汽车；第二种方案：租用起步价8元，每千米为1.4元的汽车. 按出租车管理条例,在起步价内,不同型号的车行驶的历程是相等的,则从经济角度出发此人从A地到B地应选择哪一种方案?
（22）（本小题满分14分）数列{
}的前
项和为
，
(I)若数列{+c}成等比数列，求常数c的值；
(II)求数列{}的通项公式；
(III)数列{}中是否存在三项，它们可以构成等差数列？若存在，请求出一组适合条件的
项；若不存在，请说明理由.
高考模拟考试数学（三）
参考答案（文）
一、选择题
1~5 CDABB 6~10 C BDBA 11~12 CC
二、填空
13、 160
14、
15、 540
16、 0或2或4
三、17、解：①当
即 
或
时
原式变形为
即
…………………………………4分
解得
或
∴或……………………………………………………………6分
②当
即
时
原式变形为
即
…………………………………8分
∴
…………………………………………………………………10分
综上知：原不等式解集为
或
且
…………………………12分
18、(Ⅰ)取
的中点
，连
∵，
都是边长为4的正三角形
∴
，
且
………………………………2分
∴
面
又∵
面
∴……………………………………………………………………4分
（Ⅱ）∵，
∴
为二面角
的平面角，过D作
交
于E
∵面
面ABC
∴DE⊥面ABC
∴DE是D到面ABC的距离，DO=
BD
……………………………………6分
∵DE≥3
∴
sin∠AOD≥3 
∴
…………………………………………………………8分
（Ⅲ）
=
………………10分
当∠AOD=
，四面体体积取得最小值
当∠AOD=
时，四面体体积取得最大值
………………………………12分
19、解：∵
∴
………………………………………………………2分
①∵ 即
∴
∴
…………………………………………………………4分
解之得：
∴
…………………………………………………………6分
②∵
…………………………………8分
令
在[0，1]递增
则
……………………………………………………………10分
∴
，即的值域为
……………………12分
20、解：（Ⅰ）设
，依题意知点P的轨迹是以点F（1，0）为焦点，以直线
为准线的抛物线，其轨迹方程为
…………………………………………4分
（Ⅱ）假设有在常数a满足题设
则以PF为直径的圆与直线相切
设P（
）则PF的中点M（
）到直线的距离为
，……………………………………………………………………8分
则
化简得 
…………………………………………………………10分
上式为关于y的恒等式，于是
综上知，有在常数，使得在直线上存在唯一点Q，满足PQ⊥QF
…………………………………………………………………………………………12分
21、解：设A地到B地的距离为s千米，起步价内车辆行驶的距离为
千米
显然，当
时，应选择第二种方案；……………………………………………4分
当
时，比较第一种方案应付的车费
与第二种方案
的大小；…………………………………………………………………………………8分
当
时，应选择第二种方案；
当
时，应选择第一种方案；
当
时，两种方案均可.……………………………………………………10分
综上所述，所求答案为：（1）当时，应选择第二种方案；
（2）当时，应选择第一种方案；
（3）当时，两种方案均可.………………………………………………12分
22、解：（1）当
时有：
两式相减得：
…………………………2分
………………………………………………………………………4分
又
，∴
……………………………………………………………6分
∴数列{
}是首项6，公比为2的等比数列.从而
…………………………8分
（2）由（1）知：
……………………………………10分
（3）假设数列{
}中存在三项
，它们可以构成等差数列，
只能是
，
即
………………………………………………………………………12分
、
、
均为正整数，
∴（*）式左边为奇数右边为偶数，不可能成立. 因此数列{}中不存在可以构成等差
数列的三项.……………………………………………………………………………14分