试卷类型:A
高考模拟考试(三)
数学试题(理)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页,第Ⅱ卷3至8页。考试结束后,将本是卷和答题卡一并交回.共150分,考试时间120分钟.
第Ⅰ卷(选择题 共60分)
注意事项:
1.答第Ⅰ卷前,考生必将自己的姓名、准考证号、考试科目、试卷类型(A)用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,不能答在试题卷上。
参考公式:
三角函数的积化和差公式 正棱台、圆台的侧面及公式
![]()
![]() 其中
其中![]() 、
、![]() 分别表示
分别表示
![]() 上、下底面周长,
上、下底面周长,![]() 表示斜高或母线长
表示斜高或母线长
![]() 球的体积公式
球的体积公式 ![]() 其中R表
其中R表
![]() 示球的半径
示球的半径
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)已知集合![]()
![]() ,若
,若![]() ,则
,则![]() 的值为
的值为
(A)0 (B)1 (C)、2 (D)0或1
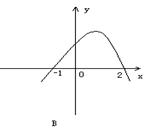
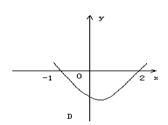
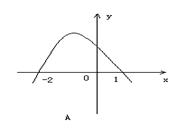
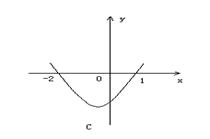 (2)不等式
(2)不等式![]() 的解集为
的解集为![]() ,则函数
,则函数![]() 的图象为
的图象为
(3)复数![]() 且
且![]() ,则
,则![]() 的一个取值区间为
的一个取值区间为
(A)(![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(4)方程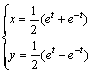 (
(![]() 为参数)化为普通方程是
为参数)化为普通方程是
(A)![]() (B)
(B)![]() (
(![]() (C)
(C)![]() (
(![]() (D)
(D)![]()
(5))函数![]() ,给出下列命题,其中正确的是
,给出下列命题,其中正确的是
(A)当![]() 时,
时,![]()
(B)函数![]() 在区间
在区间![]() 上是增函数
上是增函数
(C)函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
(D)函数![]() 的图象是由函数
的图象是由函数![]() 的图象向左平移
的图象向左平移![]() 个单位得到
个单位得到
(6)某人坐在一趟以每小时120公里由东向西行驶的火车上,发现在与火车道平行且与火车道相距1公里的笔直公路上行驶着一辆汽车,此时汽车处于北偏西![]() 处,当行驶1小时后,汽车在北偏东
处,当行驶1小时后,汽车在北偏东![]() 处,则汽车行驶的速度为
处,则汽车行驶的速度为
(A) 120 (B)![]() (C)118
(D)117
(C)118
(D)117
(7)数列![]() 满足
满足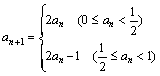 若
若![]() ,则
,则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(8)一个圆锥有三条母线两两垂直,则它的侧面展开图的圆心角为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(9)函数![]() 在区间
在区间![]() 上是增函数,则
上是增函数,则![]() 的取值范围为
的取值范围为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(10)双曲线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,若直线
两点,若直线![]() 既过双曲线的焦点,又过抛物线的焦点,则此双曲线的离心率为
既过双曲线的焦点,又过抛物线的焦点,则此双曲线的离心率为
(A) ![]() (B)
(B)![]() (C)2
(D)3
(C)2
(D)3
(11)在正三棱柱![]() 中,
中,![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成的角的大小是
所成的角的大小是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(12)13年前有一笔扶贫助学基金,将利息用于扶贫助学,每年的存款年利率为11.34%(不扣税),可资助100人上学,平均每人每月94.5元,而现在的年利率为1.98%,且扣20%的利息率税,同样资助100人上学,而现在每人每月的生活费为100元,则需要的扶贫助学资金再增加的款数约为
(A)631313 (B)83333 (C)547980 (D)
高考模拟考试(三)
数学试题(理)
第Ⅱ卷(非选择题 共90分)
注意事项:
1. 第Ⅱ卷共7页,用钢笔或圆珠笔直接答在试卷上.
2. 答卷前将密封线内的项目填写清楚.
二、填空题:本大题共4小题,每小题4分,共16分. 把答案填在题中的横线上.
(13)(0.997)![]() 的近似值(精确到0.001)为__________________.
的近似值(精确到0.001)为__________________.
(14)正方体![]() 中,
中,![]() ,线段
,线段![]() 在
在![]() 上运动,且
上运动,且![]() ,则四面体
,则四面体![]() 的体积为_____________________.
的体积为_____________________.
(15)对某种产品中的10件不同的正品和2件不同的次品,一一进行测试,到区分出所有次品为至,若所有次品中恰好在第四次测试中全部出现,则测试的方法有____________种.
(16)椭圆两焦点![]() 、
、![]() ,椭圆上满足
,椭圆上满足![]() 的点
的点![]() 个数为______________.
个数为______________.
三、解答题:本大题共6小题,共74分. 解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)函数![]() ,求
,求![]() 的最大值及取最大时
的最大值及取最大时![]() 的集合.
的集合.
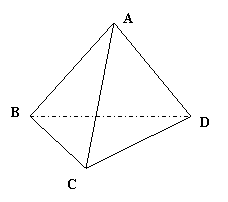 (18)(本小题满分12分)如图,四面体
(18)(本小题满分12分)如图,四面体![]() 中,
中,![]() 与
与![]() 都是边长为4的正三角形
都是边长为4的正三角形
(I)求证:![]()
(II)若点![]() 到平面
到平面![]() 的距离不小于3,求二面角
的距离不小于3,求二面角![]() 的平面角的取值范围
的平面角的取值范围
(III)当二面角![]() 的平面角为
的平面角为![]() 时,求点
时,求点![]() 到平面
到平面![]() 的距离.
的距离.
(19) (本小题满分12分)已知![]() 定义域为
定义域为![]() ,且对任意的
,且对任意的![]() 、
、![]() ,恒有
,恒有![]() ,
,![]() 时,
时,![]()
(I)求![]() 的值,并证明
的值,并证明![]()
(II)求证:在![]() 的定义域内恒有
的定义域内恒有![]()
(20)(本小题满分12分)已知动点![]() 到定点
到定点![]() 的距离比它到定直线
的距离比它到定直线![]() 的距离小1
的距离小1
(I)求动点![]() 的轨迹方程
的轨迹方程
(II)设点![]() 是①中轨迹上任意一点,试问:是否存在常数
是①中轨迹上任意一点,试问:是否存在常数![]() ,使得在直线
,使得在直线![]() 上存在唯一点
上存在唯一点![]() ,满足
,满足![]() ,若存在,求出常数
,若存在,求出常数![]() ,若不存在,请说明理由。
,若不存在,请说明理由。
(21)(本小题满分12分)某地计划从今年起填海湾围造一部分生产和生活用地,若填海湾费,购置排水设备费等所需经费与当年所填海湾造地面积![]() (亩)的平方成正比,其比例系数为
(亩)的平方成正比,其比例系数为![]() ,设每亩水面的年平均经济收益为
,设每亩水面的年平均经济收益为![]() 元,填海湾造地后的每亩土地的年平均收益为
元,填海湾造地后的每亩土地的年平均收益为![]() 元(其中
元(其中![]() 、
、![]() 、
、![]() 均为常数)
均为常数)
(I)若按计划填海湾造地,且使得今年的收益不小于支出,试求所填面积![]() 的最大值
的最大值
(II)如果填海湾造地面积按每年1%的速度减少,为保证水面的畜洪能力和环保要求,填海湾造地的总面积永远不能超过现有海湾面积的25%,求今年填海湾造地的面积最多能占现有海湾的百分之几?
(22) (本小题满分14分)我们可以证明:当![]() 时,函数
时,函数![]() 在开区间
在开区间![]() 内是增函数;当
内是增函数;当![]() 时,函数
时,函数![]() 在开区间
在开区间![]() 内是减函数.
内是减函数.
(I)若数列![]() 满足
满足![]() ,
,![]() (
(![]() 为正整数),
为正整数),
求证:![]()
(II)若数列![]() 满足
满足![]() ,
,![]() (
(![]() 为正整数),问数列
为正整数),问数列![]() 是否单调?
是否单调?
高考模拟考试数学理(三)
参考答案(理)
一、选择题(每小题5分,共60分)
1~5 BBABC 6~10 C BB AB 11~12 C D
二、填空(每小题4分,共16分)
13、 0.991 14、![]() 15、 540 16、 0或2或4
15、 540 16、 0或2或4
三、解答题
17、 ![]()
=![]()
=![]() ……………………………………………………4分
……………………………………………………4分
=![]()
=1+![]() …………………………………………………………6分
…………………………………………………………6分
![]() …………………………………………………………8分
…………………………………………………………8分
当![]() ,即
,即![]()
![]() …………………………10分
…………………………10分
∴![]() 最大值
最大值![]() ,此时
,此时![]() …………………………12分
…………………………12分
18、(Ⅰ)取![]() 的中点
的中点![]() ,连
,连![]()
∵![]() ,
,![]() 都是边长为4的正三角形
都是边长为4的正三角形
∴![]() ,
,![]() 且
且![]() …………………………………………2分
…………………………………………2分
∴![]() 面
面![]()
又∵![]() 面
面![]()
∴![]() …………………………………………………………………………4分
…………………………………………………………………………4分
(Ⅱ)∵![]() ,
,![]()
∴![]() 为二面角
为二面角![]() 的平面角,过D作
的平面角,过D作![]() 交
交![]() 于E
于E
∵面![]() 面ABC
面ABC
∴DE⊥面ABC
∴DE是D到面ABC的跑离,DO=![]() BD
BD
![]() ……………………………………………………6分
……………………………………………………6分
∵DE≥3
∴![]() sin∠AOD≥3
sin∠AOD≥3 ![]()
∴![]() …………………………………………………………………8分
…………………………………………………………………8分
(Ⅲ)由于![]() ,
,![]()
![]()
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由
,由![]() 得
得
![]() ……………………………………………………………10分
……………………………………………………………10分
所以![]()
故点![]() 到平面
到平面![]() 的距离为
的距离为![]() ………………………………………………12分
………………………………………………12分
19、(1)∵![]()
![]()
∴当![]() 时,
时,![]()
得![]() ……………………………………………………………………2分
……………………………………………………………………2分
令![]() 得
得 ![]()
∴![]()
即![]() ………………………………………………………………4分
………………………………………………………………4分
(2)∵![]() 时
时![]()
![]()
![]()
∴![]() 时,
时,![]()
![]() ……………………………6分
……………………………6分
∴![]() 在
在![]() 上单调递减……………………………………………8分
上单调递减……………………………………………8分
(3)∵对于![]() 的定义域内
的定义域内![]() 有
有
![]() ………………………10分
………………………10分
∴![]() ……………………………………12分
……………………………………12分
20、(Ⅰ)设![]() ,依题意知点P的轨迹是以点F(1,0)为焦点,以直线
,依题意知点P的轨迹是以点F(1,0)为焦点,以直线![]() 为准线的抛物线,其轨迹方程为
为准线的抛物线,其轨迹方程为![]() …………………………………………4分
…………………………………………4分
(Ⅱ)假设有在常数a满足题设
则以PF为直径的圆与直线![]() 相切
相切
设P(![]() )则PF的中点M(
)则PF的中点M(![]() )到直线
)到直线![]() 的距离为
的距离为
![]() ,…………………………………………………………………8分
,…………………………………………………………………8分
则![]()
![]()
化简得 ![]() …………………………………………………………10分
…………………………………………………………10分
上式为关于y的恒等式,于是![]()
综上知,有在常数![]() ,使得在直线
,使得在直线![]() 上存在唯一点Q,满足PQ⊥QF
上存在唯一点Q,满足PQ⊥QF
…………………………………………………………………………………………12分
21、填海湾面积![]() (亩),填海湾及排水设备费
(亩),填海湾及排水设备费![]() (元),水面经济收益
(元),水面经济收益![]() ,填海湾造地后收益
,填海湾造地后收益![]() …………………………………………………………………2分
…………………………………………………………………2分
(Ⅰ)收益不小于支出的条件可以表示为
![]() ………………………………………………………………………4分
………………………………………………………………………4分
所以![]()
当![]() 即
即![]() 时,不能填海湾造地
时,不能填海湾造地
当![]() 即
即![]() 时,此时所填面积的最大值为
时,此时所填面积的最大值为![]() 亩…………………6分
亩…………………6分
(Ⅱ)设该地现有水面![]() 亩,今年填海湾造地
亩,今年填海湾造地![]() 亩则
亩则
![]() ……………………………………………8分
……………………………………………8分
不等式左边也是无穷等比数列(首项为![]() ,公比
,公比![]() )的和
)的和
故有![]() 即
即![]() ………………………………………………10分
………………………………………………10分
因此,今年海湾造地面积最多只能占现有水面的0.25%…………………………12分
22、(Ⅰ)由题设知,当![]() 时,
时,![]()
假设当![]() 时,有
时,有![]() 则
则
当![]() 时,有
时,有![]()
且![]()
(因为![]() 在(0,1)上是增函数)
在(0,1)上是增函数)
∴![]() 时命题成立,故
时命题成立,故![]() 为正整数……………………………6分
为正整数……………………………6分
又∵![]()
∴![]() …………………………………………………………………8分
…………………………………………………………………8分
(Ⅱ)数列![]() 不具有单调性
不具有单调性
令![]() 则
则![]()
![]()
∴![]() …………………………………………………………………………10分
…………………………………………………………………………10分
而![]() (因为
(因为![]() 在(0,1)上是减函数)
在(0,1)上是减函数)
∴![]()
∴数列![]() 不具有单调性………………………………………………………14分
不具有单调性………………………………………………………14分