高考数学卷（理）
一、选择题：本大题共12小题，每小题5分，满分60分。
1．
若U={1,2,3,4}，M={1,2},
N={2,3}, 则
(M
N)=
(A){1,2,3} (B){2} (C){1,3,4} (D){4}
2．
点P从(1,0)出发，沿单位圆x2+y2=1按逆时针方向运动
弧长到达Q点，则Q的坐标为
(A)(-
,
) (B) (--) (C)(-,-) (D)(-,)
3．
已知等差数列{an}的公差为2，若a1,a3,a4成等比数列，则a2=
(A)-4 (B)-6 (C)-8
(D)-10
4．
曲线y2=4x关于直线x=2对称的曲线方程是
(A)y2=8-4x (B)y2=4x-8 (C)y2=16-4x (D)y2=4x-16
5．
设z=x-y, 式中变量x和y满足条件
， 则z的最小值为
(A)1 (B)-1 (C)3 (D)-3
6．
已知复数z1=3+4i,
z2=t+i, 且
是实数，则实数t=
(A)
(B)
(C)-
(D)-
7．
若
展开式中存在常数项，则n的值可以是
(A)8 (B)9 (C)10 (D)12
8．
在△ABC中，“A＞30°”是“sinA＞”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件
(D)既不充分也不必要条件
9．
若椭圆
(a＞b＞0)的左、右焦点分别为F1、F2，线段F1F2被抛物线y2=2bx的焦点分成5∶3的两段，则此椭圆的离心率为
(A)
(B)
(C)
(D)
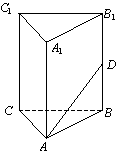
10．如图，在正三棱柱ABC-A1B1C1中，已知AB=1，D在棱BB1上，且BD=1，若AD与平面AA1C1C所成的角为a，则a=
(A)
(B)
(C)
(D)
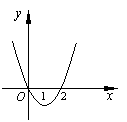
11．设f '(x)是函数f(x)的导函数，y=f '(x)的图象如右图所示，则y=f(x)的图象最有可能的是
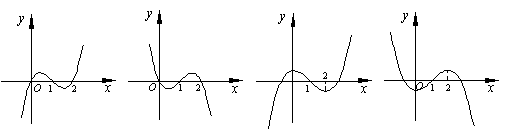
(A) (B) (C) (D)
12．若f(x)和g(x)都是定义在实数集R上的函数，且方程x-f[g(x)]=0有实数解，则g[f(x)]不可能是
(A)x2+x-
(B)x2+x+ (C)x2- (D)x2+
二、填空题：本大题共4小题，每小题4分，满分16分。把答案填在题中横线上。
13．已知f(x)=
,则不等式x+(x+2)·f(x+2)≤5的解集是__________.
14．已知平面上三点A、B、C满足
=3, 
=4, 
=5，则
的值等于________.
15．设坐标平面内有一个质点从原点出发，沿x轴跳动，每次向正方向或负方向跳1个单位，经过5次跳动质点落在点（3，0）（允许重复过此点）处，则质点不同的运动方法共有__________种（用数字作答）.
16．已知平面a与平面b交于直线l，P是空间一点，PA⊥a，垂足为A，PB⊥b，垂足为B，且PA=1，PB=2，若点A在b内的射影与点B在a内的射影重合，则点P到l的距离为________.
三、解答题：本大题共6小题，满分74分。解答应写出文字说明证明过程或演算步骤。
17． (本题满分12分)
在△ABC中，角A、B、C所对的边分别为a,b,c，且cosA=
(Ⅰ)求sin2
+cos2A的值；
(Ⅱ)若a=
,求bc的最大值。
18．
(本题满分12分)
盒子中有大小相同的球10个，其中标号为1的球3个，标号为2的球4个，标号为5的球3个。第一次从盒子中任取1个球，放回后第二次再任取1个球（假设取到每个球的可能性都相同），记第一次与第二次取到球的标号之和为x。
（1）求随机变量x的分布列；
（2）求随机变量x的期望Ex。
19．如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=
，AF=1，M是线段EF的中点。
（1）求证AM//平面BDE；
（2）求二面角A-DF-B的大小；
（3）试在线段AC上确定一点P，使得PF与BC所成的角是60°。
20．设曲线y=e-x(x≥0)在点M(t,e-t}处的切线l与x轴、y轴围成的三角形面积为S(t).
(1)求切线l的方程；
(2)求S(t)的最大值。
21．已知双曲线的中心在原点，右顶点为A(1,0)，点P、Q在双曲线的右支上，点M(m,0)到直线AP的距离为1，
（1）若直线AP的斜率为k，且kÎ[
], 求实数m的取值范围；
（2）当m=
+1时，△APQ的内心恰好是点M，求此双曲线的方程。
22．
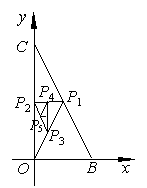如图，△OBC的三个顶点坐标分别为(0,0)、(1,0)、(0,2)，设P1为线段BC的中点，P2为线段CO的中点，P3为线段OP1的中点，对于每一个正整数n，Pn+3为线段PnPn+1的中点，令Pn的坐标为(xn,yn)，an=yn+yn+1+yn+2.
（1）求a1,a2,a3及an；
（2）证明
,nÎN*;
（3）若记bn=y4n+4-y4n,nÎN*，证明{bn}是等比数列。