高考数学第一次月考试题
集合 简易逻辑 函数
一选择题(每题5分,共60分)
1.设f(x)、g(x)都是单调函数,有如下四个命题:
①若f(x)单调递增,g(x)单调递增,则f(x)-g(x)单调递增;
②若f(x)单调递增,g(x)单调递减,则f(x)-g(x)单调递增;
③若f(x)单调递减,g(x)单调递增,则f(x)-g(x)单调递减;
④若f(x)单调递减,g(x)单调递减,则f(x)-g(x)单调递减;其中,正确的命题是 ()
A.①③ B.①④ C.②③ D.②④
2.设f(x)是(-∞,+∞)上的奇函数,f(x+2)=-f(x),当0≤x≤1时,f(x)=x,则f(7.5)=( )
A.0.5 B.-0.5 C.1.5 D.-1.5
3.已知映射f:A→B,其中,集合A={-3,-2,-1,1,2,3,4},集合B中的元素都是A中元素在映射f下的像,且对任意的a∈A,在B中和它对应的元素是a,则集合B中元素的个数是( )
A.4 B.5 C.6 D.7
4.集合A={a2,a+1,-1},B={2a-1, a-2 , 3a2+4},A∩B={-1},则a的值是( )
A.-1 B.0 或1 C.2 D.0
5.己知关于x的方程(m+3)x2-4mx+2m-1=0的两根异号,且负根的绝对值比正根大,那么实数m的取值范围是 ( )
A.-3<m<0 B.m<-3或m>0
C.0<m<3 D.m<0 或 m>3
6.有下列四个命题:
①“若x+y=0 ,则x ,y互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若q≤1,则x2+2x+q=0有实根”的逆否命题;
④“不等边三角形的三个内角相等”逆命题;
其中的真命题为 ( )
A.①② B.②③ C.①③ D.③④
7.命题p:若A∩B=B,则![]() ;命题q:若
;命题q:若![]() ,则A∩B≠B.那么命题p与命题q的关系是
( )
,则A∩B≠B.那么命题p与命题q的关系是
( )
A.互逆 B.互否 C.互为逆否命题 D.不能确定
8.a=log0.70.8,b=log1.10.9,C=1.10.9,那么( )
(A)a<b<c (B)a<c<b (C)b<a<c (D)C<a<b
9.函数y=a-![]() 的反函数是( )
的反函数是( )
(A)y=(x-a)2-a (x![]() a)
(B)y=(x-a)2+a (x
a)
(B)y=(x-a)2+a (x![]() a)
a)
(C)y=(x-a)2-a (x![]() )
(D)y=(x-a)2+a (x
)
(D)y=(x-a)2+a (x![]() )
)
10、函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() 的递增区间为()
的递增区间为()
A.
(-2,2) B.
![]() C.
C.
![]() D.
D.
![]()
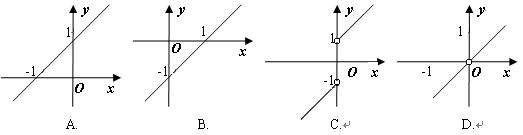
11、已知函数![]() ,则其图象为()
,则其图象为()
12、设![]() 是R上的奇函数,且当
是R上的奇函数,且当![]() 时
时![]() ,则当
,则当![]() 时
时![]() 的表达式为( )
的表达式为( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
二、填空题:(每题4分,共16分)
13.方程![]() 的解是______________
的解是______________
14.若对于任意a![]() [-1,1], 函数f(x) = x
[-1,1], 函数f(x) = x![]() + (a-4)x + 4-2a的值恒大于零, 则x的取值范围是
.
+ (a-4)x + 4-2a的值恒大于零, 则x的取值范围是
.
15.定义运算法则如下:
a![]() 则M+N=
则M+N=
16.如果函数f(x)的定义域为R,对于![]() 是不大于5的正整数,当x>-1时,f(x)>0. 那么具有这种性质的函数f(x)=
.(注:填上你认为正确的一个函数即可)
是不大于5的正整数,当x>-1时,f(x)>0. 那么具有这种性质的函数f(x)=
.(注:填上你认为正确的一个函数即可)
三.解答题(17-21题,每题12分,22题14分,共74分)
(17)解关于x的不等式![]()
.
18 已知实数![]() 满足不等式
满足不等式![]() ,试判断方程
,试判断方程![]() 有无
有无
实根,并给出证明.
19某村计划建造一个室内面积为800![]() 的矩形蔬菜温室。在温室内,沿左、右两端与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左、右两端与后侧内墙各保留1![]() 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3![]() 宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
20 记函数f(x)=![]() 的定义域为A, g(x)=lg[(x-a-1)(2a-x)](a<1) 的定义域为B.(1) 求A;
的定义域为A, g(x)=lg[(x-a-1)(2a-x)](a<1) 的定义域为B.(1) 求A;
(2) 若B![]() A, 求实数a的取值范围.
A, 求实数a的取值范围.
21. 如果函数![]() 在区间D上都是增函数,那么函数
在区间D上都是增函数,那么函数![]() 在区间D上也是增函数。设
在区间D上也是增函数。设![]()
(I)求函数![]() 的定义域;
的定义域;
(II)求函数![]() 的值域。
的值域。
22、已知f(x)=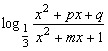 。是否存在实数p、q、m,使f(x)同时满足下列三个条件:①定义域为R的奇函数;
。是否存在实数p、q、m,使f(x)同时满足下列三个条件:①定义域为R的奇函数;
②在[1,+∞)上是减函数;
③最小值是-1。
若存在,求出p、q、m;若不存在,说明理由。
参考答案
一选择题
1C,2B,3A,4D,5A,6C,7C,8C,9D,10C,11C,12A
二填空题
13![]() 14,(-∞‚1)∪(3,+∞) 15, 5. 16.
x+6或2x+6或3x+6或4x+6或5x+6
14,(-∞‚1)∪(3,+∞) 15, 5. 16.
x+6或2x+6或3x+6或4x+6或5x+6
三.解答题
(17) 解:原不等式化为![]() ………………3分
………………3分
若![]() ,有
,有![]() ,原不等式的解集为
,原不等式的解集为![]() ;
;
若![]() ,有
,有![]() ,原不等式的解集为
,原不等式的解集为![]() ;
;
若![]() ,有
,有![]() ,原不等式的解集为
,原不等式的解集为![]() 或
或![]() ………………12分18.解:(Ⅰ)
………………12分18.解:(Ⅰ)![]() 等价于
等价于 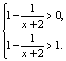 解得
解得![]() …………5分
…………5分
方程![]() 的判别式
的判别式
![]() …………9分 ∵
…………9分 ∵![]()
由此得方程![]() 无实根.…………13分
无实根.…………13分
18.解:(Ⅰ)![]() 等价于
等价于 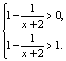 解得
解得![]() …………5分
…………5分
方程![]() 的判别式
的判别式
![]() …………9分 ∵
…………9分 ∵![]()
由此得方程![]() 无实根.…………13分
无实根.…………13分
 20、【解】(1)2-
20、【解】(1)2-![]() ≥0, 得
≥0, 得![]() ≥0, x<-1或x≥1
≥0, x<-1或x≥1
即A=(-∞,-1)∪[1,+ ∞)
(2) 由(x-a-1)(2a-x)>0, 得(x-a-1)(x-2a)<0.
∵a<1,∴a+1>2a, ∴B=(2a,a+1).
∵B![]() A, ∴2a≥1或a+1≤-1, 即a≥
A, ∴2a≥1或a+1≤-1, 即a≥![]() 或a≤-2, 而a<1,
或a≤-2, 而a<1,
∴![]() ≤a<1或a≤-2,
故当B
≤a<1或a≤-2,
故当B![]() A时, 实数a的取值范围是(-∞,-2)∪[
A时, 实数a的取值范围是(-∞,-2)∪[![]() ,1]
,1]
21 解:(I)函数![]() 应满足
应满足
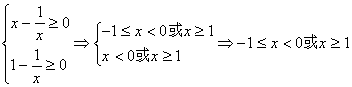 3分
3分
所以![]() 的定义域为
的定义域为![]() 4分
4分
(II)函数![]() 时是增函数,证明如下:
时是增函数,证明如下:
设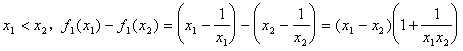
当![]() 时,
时,![]()
所以![]()
则函数![]() 或
或![]() 时是增函数 7分
时是增函数 7分
又函数![]() 时是增函数,证明如下:
时是增函数,证明如下:
设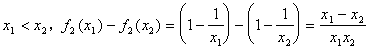
当![]()
所以![]()
函数![]() 时是增函数 9分
时是增函数 9分
则![]() 时是增函数
时是增函数
当![]() 11分
11分
函数![]() 的值域为
的值域为![]() 13分
13分
22、∵f(x)是奇函数 ∴f(0)=0 得q=1
又f(-x)=-f(x) ∴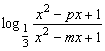 =-
=-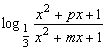
![]() =
=![]() 即(x2+1)2-p2x2=(x2+1)2-m2x2
即(x2+1)2-p2x2=(x2+1)2-m2x2
∴p2=m2
若p=m,则f(x)=0,不合题意。故p=-m≠0
∴f(x)=![]()
由f(x)在[1,+∞)上是减函数,令g(x)=![]() =1-
=1-![]() =1-
=1-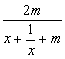
∵![]() 在[1,+∞)上递增,在(-∞,-1]也递增,只有m>0时,在[1,+∞)上g(x)递增,从而f(x)递减。
在[1,+∞)上递增,在(-∞,-1]也递增,只有m>0时,在[1,+∞)上g(x)递增,从而f(x)递减。
∴x=-1时,![]() 在(-∞,-1]上取得最大值-2,此时由f(x)的最小值为-1得g(x)的最大值为3。
在(-∞,-1]上取得最大值-2,此时由f(x)的最小值为-1得g(x)的最大值为3。
1-![]() =3 得m=1,
=3 得m=1,
从而p=-1
∴存在p=-1,q=1,m=1。