集合、子集

　　　　　　　　　　　　　　　　　　 集合、子集

一、学习目标

　1.理解集合的概念．

　2.掌握集合的表示法：列举法、描述法、图示法．

　3.理解子集的概念，掌握“属于、包含、相等”三种关系的有关术语和符号，形成正确、简明的集

　　合语言．

二、例题

　　　　　　　　　　　　　　　　　　　  第一阶梯

1.什么是集合、集合的元素？怎样表示元素与集合的关系？集合有哪些基本性质？

参考答案：

　　一组对象的全体，就形成一个集合．集合里的各个对象叫做集合的元素．集合用大写拉丁字母表示，

　　如N、Z、Q等．元素用小写拉丁字母表示，如a．

　　集合和元素的关系是“属于”和“不属于”的关系，其符号是“∈”和“”．，如a是集合A的元素，

　　记作a∈A，如果a不是集合B的元素，记作aB．

　　集合的元素有两个基本性质：

　　(1)确定性 对于集合A和元素x有明确的关系，是x∈A，还是xA，二者必居其一．

　　(2)互异性 在同一集合中，任何两个元素必须是不同的，相同的元素，只能算作一个．例如方程x²＋

　　　 2x＋1=0有相等二根：x₁=－1，x₂=－1，但在集合语言，方程x²＋2x＋1=0的解集应是{－1}，而不

　　　 可写为{－1，－1}．

　　　 任何集合的元素都有上述两个共性，所以我们把元素的确定性和互异性称为集合的基本性质．

说明：

　　集合和元素是最原始的不定义概念，就和“点”、“线”、“面”一样，都是不加定义的．因此，你

　　不要追求集合的严格定义，只能用它的两个基本性质理解它．由元素的确定性和互异性，必然推出集

　　合的元素具有无序性，例如，{1，2，3}={1，3，2}．

　　请记住常用数集的代号：

　　N={自然数}={正整数}， Z={整数}，

　　Q={有理数}，Q^＋={正有理数}，

　　R={实数}，R^＋={正实数}

2.怎样表示集合？

　参考答案：

　

3.什么叫子集、等集、真子集？什么叫空集？

　参考答案：

　　任意的xÎ A ÞÞ xÎB，则称A是B的子集，记作AÍB，读作A包含于B，或说B包含A．

　　如果AÍB，且BÍ A，则称A=B．

　　如果AÍB，且A≠ B，则称A是B的真子集，记作AÌB，不含任何元素的集合叫做空集，记作f ．

说明：

　　(1)关于子集和真子集有下列推论：

　　　①AÍB ÞAÌB或A=B，且二者必居其一；

　　　②AÌB ÞÞ AÍB；

　　　③AÍA（A是任何集合）；

　　　④规定f ÍA（A是任何集合）．

　　(2)子集与真子集是集合与集合的包含关系，等集是集合与集合的相等关系．“包含”与“相等”关

　　　 系都是集合与集合的关系，它们和元素与集合的关系不同，后者是属于（ÎÎ ）与不属于（ÏÏ ）

　　　 的关系．“包含”、“相等”、“属于”是重要的三大关系，易错易混，要注意区分．

　　　　　　　　　　　　　　　　　　　　　 第二阶梯

1. 化简下列集合：

　　(1){x x=x²}；

　　(2){x )} ;

　　(3){不超过10的质数}．

[提示] 

　　用列举法来化简集合．

[参考答案]

　　(1){x x=x2}={－1, 0, 1}.

　　(2)原集合化简为{－1，}．

　　(3)原集合化简为{2，3，5，7}．

[说明]

　　　列举法具有化简有限集合的功能．

2.已知集合A{x, xy, xy－1} , xÎZ , yÎZ , 且y≠0. 如果0ÎA，求A．

[提示]

　　　利用集合元素的互异性，分类讨论

[参考答案]

　　 由0ÎA，y≠0 ÞÞ x=0，或xy－1=0.

　　 若x=0 , 则xy=0 , 此时A中的元素x、xy相同，所以x≠0．

　　 若xy－1=0，由于x , y ÎZ，所以x=y=1，或x=y=－1．

　　 当x=y=1时，A={1，1，0}P这与元素互异相矛盾，因此，只能x=y=－1．

　　 所以，A={－1，1，0}．

3.下列命题中，正确的是（ ）．

　　(A) R^＋Î R　　(B) Z^＋ÉÉ{x x≥0 , xÎZ}　　 (C)空集是任何集合的真子集　 (D) f Î {f }

[提示]

　　　　(A)中R^＋不是元素，R^＋与R的关系是包含关系，不是属于关系.

　　　　(B) 0Î{x x≥0 , xÎ Z},但0ÏZ^＋.

　　　　(C)当任何集合为空集时，即为反例.

　　　　(D){f}表示以空集f为元素的集合，故（D）正确．

[参考答案]（D）

4.已知A={x 1≤x≤2} , B={x (x－1)(x－a)≤0 , aÎ R} , 且AÌB，求实数a的取值集合

[提示]

　　用数轴表示数集A，B，比较端点，即可解．

[参考答案] 

　　　A={x 1≤x＜2＝．如图4．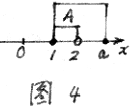

对于B：当a=1时，B={1}，此时AÌ B无解；

当a＜1时，B={x a≤x≤1} ，此时AÌB也无解；

当a＞1时，B={x 1≤x≤a}，此时AÌB，得解a≥a，综上，a的取值集合是{a a≥2}．

[说明]

　　　用数轴表示集合是集合的一种图示法，属于数形结合法，是解决集合问题的好方法．

　　　　　　　　　　　　　　　　　　　　  第三阶梯

1.判定下列A和B的关系：

　　　（1）

　　　（2）

　　　（3）

　　　（4）

[提示]

　　　　 利用子集、真子集和等集的概念解题．

[参考答案]

　　　　（1）因为．

　　　　（2）因为A=φ，所以A=B．

　　　　（3）A={x x≥3}，B={y y≥1}，所以AÉ B．

　　 　 （4）

　　　　　 　

[说明]

　　判定两个集合之间的关系的通法：通过元素与集合的关系（），确定集合与集合的关系

　　（）；数形结合，用图示法．注意集合的列举法、描述法和图示法三法之间的相互转化，

　　其中描述法较难，常将描述法转化为列举法或图示法．

2.（1）列出下列集合的所有子集：

　　　．

　（2）试猜想有限集的子集个数

[提示]

　　　（1）根据子集的定义，一一列举各集合的子集，注意列举和计数的规律．

　　　（2）根据（1），用归纳法猜测．

　

[参考答案]

　　　　 （1）A₁的子集：φ，

　　　　　　  A₂的子集：φ，，，

　　　　 （2）由（1）可知：A₁，A₂，A₃的子集个数分别为2¹，2²，2³．

∴猜想A_n的子集个数为2ⁿ．

三、练习题

1．方程组 （ ）

　　 A．　　 B.　　　C.　　　 D.

2．已知，，．

　 如果a∈M₀，b∈M₁，c∈M₂,那么a+b-c∈

　  A．　　B．　　 C．　　 D．

3． =

　  A．　B．　　 C．　　　 D．

4．集合M={1，2}，P={x ax－1=0}，若PÌ　M，则满足条件的实数a的个数是（ ）

　  A．无穷多　　　 B．3　　　　C．2　　　 D．1

5．集合{12的正因数}用列举法表示为 　　　　　　　　　　　　　

6．集合{1，2，3}的所有真子集是 　　　　　　　　　　　 

7.一次函数y=2x－2的图象与坐标轴的交点的集合是 　　　　　　　

8. 若{x (a+1)x>a+1,a∈R}={x x<1}，那么a的取值范围是　　　　　 

9. 已知集合A={x x²+x－2=0}, B={x (x²+x－2)(x²+ax+4)=0}，如果AÌ B，那么实数a的取值集合

　  是 　　　　　　

10.一次函数y=2x－2的图象与坐标轴的交点的集合是________________

11.若{x (a+1)x>a+1,a∈R}={x x<1}，那么a的取值范围是________________

12．已知集合A={x x²+x－2=0}, B={x (x²+x－2)(x²+ax+4)=0)，如果AÌ B，那么实数a的取值集合

　  是_______________

答案：

　  1---4　　 C，C，D，B

　  5. {1，2，3，4，6，12}

　  6. φ，{1}，{2}，{3}，{1，2}，{1，3}，{2，3}

　  7. {（1，0），（0，－2）}

　  8. a < －1

　  9. {a a>4，或a≤－4}

　  10．{（1，0），（0，－2）}

　  11．a < －1

　  12．{a a>4，或a≤－4}