高三数学测试题
—集合与函数
一、选择题（本题每小题5分，共60分）
（1）已知集合
，集合
，则
是 ( )
(A) 
(B) 
(C) 
(D) 
（2） a、b为实数，集合
，
，
表示把集合M中的元素
映射到集合N中仍为，则a+b ( )
(A)
(B) 0
(C) 1
（D） 
（3）已知函数
，那么
的值为
( )
（A）9
（B）
（C）-9 （D）
（4）设
,若
、
且
，则下列不等式必定成立的是
（ ）
（B）
（C）
（D）
（5）函数 y=－x(x+2)(x≥0)的反函数定义域为 （ ） （A）
（B）
（C）
（0，1） （D）
（6）设函数
表示除以3的余数,对
都有
( )
(A) 
(B)
(C) 
(D)
(7)函数
的图象是
( )
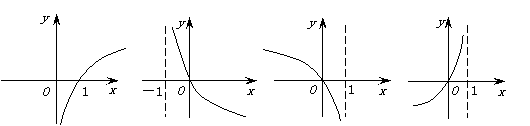(A)
(B) (C)
(D)
（8）设函数f (x)＝ax2＋bx＋c对任意实数t都有f (2＋t)＝ f (2－t)成立，在函数值f (－1)，f (1)，f (2)，f (5)中的最小的一个不可能是 ( )
(A) f (－1) (B) f (1) (C) f (2) (D) f (5)
（9）已知函数
，则 ( )
(A) 
(B) 
(C) 
(D) 
（10）由等式
定义
，则
等于 （ ）
（
）
（
）
（
）
（
）
（11）若方程
有正数解，则实数
的取值范围是 （ ）
（A）
（B）
（C）
（D）
（12）二次函数
满足
, 又
,
.若在
有最大值3, 最小值1, 则
的取值范围是 （ ）
（A）
（B）
（C）
（D）
二、填空题（本题每小题4分，共16分）
（13）函数
的图象与
的图象关于直线y=x对称，则
的递减区间是
．
（14）已知函数
是奇函数，当
时，
，且
，则a等于 ．
（15）函数f(x)满足
写出一个满足上述条件的函数_______．
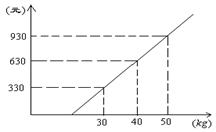（16）某航空公司规定，乘机所携带行李的重量（kg）与其运费（元）由如图的一次函数图像确定，那么乘客免费可携带行李的最大重量为 ______ ______.
三、解答题（本题17—21小题每题12分，22小题14分，共74分）
（17）已知集合
, 若
, 试证明 
.
（18）给定函数
.
（Ⅰ）求.
； （Ⅱ）判断的奇偶性，并证明你的结论.
（19）已知函数f(x)＝a＋
(a，b为实常数)
(I) 若a＝2，b＝－1，求f(x)的值域．
(II) 若f(x)的值域为[0，＋∞)，求常数a，b应满足的条件．
（20）某校校长暑假将带领该校市级“三好生”去北京旅游。甲旅行社说：“如果校长买全票一张，则其余学生可享受半价优待。”乙旅行社说：“包括校长在内，全部按全票价的6折(即按全票价的60%收费)优惠。”若全票价为240元.
(I)设学生数为x，甲旅行社收费为
，乙旅行社收费为
，分别计算两家旅行社的收费(建立表达式)；
(II)当学生数是多少时，两家旅行社的收费一样；
(III)就学生数x讨论哪家旅行社更优惠.
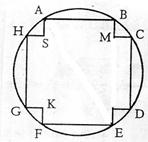
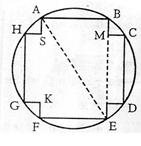
（21）有一种变压器，铁芯的截面是正十字形（如图（5）），其中矩形ABEF与矩形CDGH全等，且AS=KF=HS=MC，为保证所需的磁通量，要求正十字形面积为
，为了使绕铁芯的铜线最省，即正十字形外接圆周长最小，正十字形的AB、BE长度应各为多少cm?
|
(22) 定义在
上的函数f(x)，对于任意的
，都有
成立，当
时，
.
（Ⅰ）计算
；
（Ⅱ）证明f (x)在上是减函数；
（Ⅲ）当
时，解不等式
.
高三数学函数测试题1参考答案
一、(1)C. (2)C. (3)B. (4)C. (5)B. (6)A. (7)C. (8)B. (9)B. (10)D. (11)D. (12)D.
二、(13)（0，1
. (14)5. (15)f(x)＝
等. (16)19kg.
三、(17)因为,所以知存在
,使得
, 
.
于是 
显然
, 故知 
.
(18)（Ⅰ）令
, 解得
.
又
, 所以
, 则
,
故 
.
（Ⅱ）因为
,
所以
为奇函数.
(19)(I) ∵ x2＋2x－1＝(x－1)2－2≥－2，∴
≥0,
∴ f(x)的值域为[2，+∞]．
(II)当a＝0时，则须x2＋b的最小值≤0，∴b≤0 ;
当a≠0时，只须a＜0，且x2＋ax＋b＝
的最小值
＝a2，
即4b＝5a2. ∴ a＝0，b≤0或a＜0，4b＝5a2 .
(20)(I)=120x+240, =240·60%(x+1)=144x+144.
(II)根据题意，得120x+240=144x+144, 解得 x=4.
答：当学生人数为4人时，两家旅行社的收费一样多.
(III)当>，120x+240>144x+144， 解得 x<4;
当<, 120x+240<144x+144, 解得 x>4.
答：当学生人数少于4人时，乙旅行社更优惠；当学生人数多于4人时，甲旅行社更优惠.
(21)设AB=x，BE=y，连AE，则AE为直径，令为d，要使外接圆周长
|
,
而S□ABEF+2S□CDNM=
,
得：
,
,
上式等号成立时有
.
故当正十字形的AB为2cm，BE为（1+
）cm时，绕铁芯的铜线最省.
(22)（Ⅰ）
.
（II）设
, 因为
即
,所以
.
因为，则
，而当时，, 从而
于是在上是减函数.
（Ⅲ）因为
, 所以
,
因为在上是减函数，所以
,
解得 
或
,
故所求不等式的解集为
或
.