高考预测
将三角形的周长和面积同时平分的直线
问题 已知三角形三边长分别为4，6，8，那么同时平分这个三角形的周长和面积的直线有几条呢？
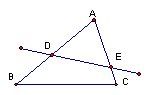
一般地，如图，直线L将
ABC的周长和面积都平分，L与边AB,AC分别交于D,E点，设m=AD, n=AE, 其内角A为
，三角形面积为，半周长为s, 则
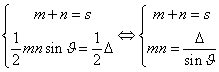
说明m,n 是关于x的方程
的两根，它有实数解的充要条件为
是否任意一个三角形都存在这样的直线L呢？若存在，最多有几条？
关于三角形的面积与半周长s平方的比的上下界, 有命题：
。（证明略）
因为任意一个三角形的三个内角中至少有一个内角不小于60º，也就是说必有（至少有一个）一个内角使得
下面我们来分析本文开头的问题：
这里，s=9, 
.
该问题有解
这里 sinB=
; 
(1) 若
， 则
m,n是方程
的两根，
。
在边BC, BA上分别取点E，D使BE=
, 直线DE即为所求。
（2）若
，则
m,n是方程
的两根，
，
说明在线段AC（角A的夹边的较长边）上找不出点F使得
，所以满足条件的解不存在。
（3）若
C, 
, 无解。
综合，满足题设条件的直线L只有一条，即情形（1）所示。