交集、并集、补集、全集
一、学习内容：
1.理解交集、并集、全集与补集的概念。
2.熟悉交集、并集、补集的性质，熟练进行交、并、补的运算
二、例题
第一阶梯
例1、什么叫集合A、B的交集？并集？
答案：
交集：A∩B={x x∈A , 且x∈B}
并集：A∪B={x x∈A , 或x∈B}
说明：
上面用描述法给出的交集、并集的定义，要特别注意逻辑联结词"且"、"或"的准确意义，在交集中
用"且"在并集中用"或交、并运算有下列推论：
例2、什么叫全集？补集？
答案：
在研究集合与集合的关系时，相对于所研究的问题，存在一个集合I，使得问题中的所有集合都是I的
子集，我们就把集合I看作全集，全集通常用I表示。
补集：
。
说明：
全集和补集都是相对的概念。全集相对于所研究的问题，我们可以适当地选取全集，而补集又相对于
全集而言。如果全集改设了，那么补集也随之而改变。为了简化问题可以巧设全集或改设全集，"选
取全集"成为解题的巧妙方法。
补运算有下列推论：①
；②
；③
。
例3、(1)求证：
，
。
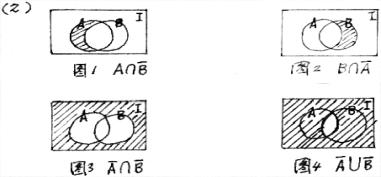
(2)画出下列集合图（用阴影表示）：
①
； ②
； ③
； ④
。
提示：
(1)证明两个集合M和P相等可分两步完成：第一步证明"由x∈M
T
x∈P"；第二步证明"由x∈P
Tx∈M "。
(2)利用（1）的结果画③、④。
答案：
说明：
(1)中的两个等式是集合的运算定律，很容易记住它，解题时可以 应用它。这个证明较难，通常不作
要求。
但其证明是对交、并、补运算及子集的很好练习。
(2)中的四个集合图也是集合的图示法的很好练习。图(1)叫做"左月牙"，图2叫做"右月牙"。画图3、
图4时要利用集合的两个运算律来画。
第二阶梯
例1、已知A={x 2x4＋5x3－3x2=0}，B={x x2＋2x－15=0}，求A∩B，A∪B。
[提示]
先用列举法化简集合A和B。
[答案]
由2x4＋5x3－3x2=0得x=0，或2x2＋5x－3=0，
∴x=0，或x=－3，或x=，
∴A={－3，0， }
由x2＋2x－15=0得x=3或x=－5，
∴x= ±3，即得B={－3，3}。
∴A∩B={－3}，A∪B={－3，0，
，3}
例2、设全集I={2，3，a2＋2a－3} , A={2 , 2a－1} , ={5} , 求实数a的值。
答案：
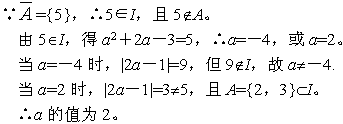
说明：
例3、设全集I={1，2，3，…9}，
={3，8}，
={2，5}，
={1，2，3，5，6，7，8}，
求集合A，B。
[答案]
说明：
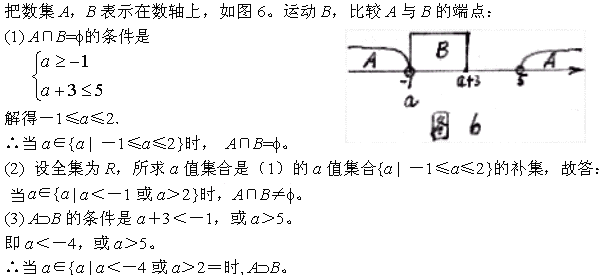
例4、设A={x x>5或x<－1} , B={x a≤x≤a＋3}，试问实数a为何值时，
(1) A∩B=φ；(2) A∩B≠φ；(3) A
B。
答案：
说明：
数形结合在集合中有两个方法：一是画集合图，如例3；二是利用坐标系，如本例画数轴（数轴是
一维的坐标系）。这两个方法总括为集合的图示法，即寻求集合与图形的对应，找到直觉。从而把
抽象的集合问题具体化和形象化
此外，本题之（二）的解法是补集法，省去了多少烦恼！
第三阶梯：
例1、设全集I={(x , y) x , y∈R}，集合M={(x , y) 
}，N={(x , y) y=3x－2}，那
么
等于（ ）。
(A) φ (B) (2 , 4) (C) {(2 , 4)} (D) N
提示：
先等价化简集合M，再用坐标平面内的点集理解集合M与N的关系。
答案：
，
∴M={(x , y) y=3x－2，且x≠2}，
∴N=M∪{(2 , 4)}
∴
={(2
, 4)}，故选（C）。
说明：
本题是数形结合法的范例，用点集来理解抽象的集合M、N的关系就十分清晰、直观。解题的关键是
分清M和N的关系，当找到N=M∪{(2 , 4)}时，问题便迎刃而解。此外，注意单元素集合{(2,4)}和元素
（2, 4）不同，所以选（B）是错误的。
例2、据统计我校高中一年级的100名学生中，爱好体育的学生有75人，爱好文艺的学生有56人，试问文
艺、体育都爱好的学生最多有多少人？最少有多少人？
提示：
利用集合图列出各种爱好者的人数间的函数关系。
答案：
设A={爱好体育的学生}，B={爱好文艺的学生}，
则A∩B={文艺、体育都爱好的学生}，
A∪B={爱好文艺或爱好体育的学生}。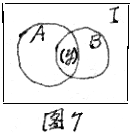
我们把有限集合M的元素个数记作card(M)，card(A)=75，
card(B)=56，card(A∩B)=y , card(A∪B)=x。于是由集合图（图7）
得 x=75＋56－y (75≤x≤100)
即 y=131－x (75≤x≤100)
∴31≤y≤56。
答：文艺、体育都爱好的学生最多有56人，最少有31人。
说明：
关于有限集合的并、交的元素个数的问题，用图解法解决具有无比的优越性。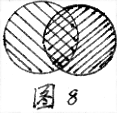
一般地，对于任意两个有限集合A , B有
card(A∪B)=card(A)＋card(B)－card(A∩B).
其道理可由图8看出来。
对于任意的三个有限集合A，B，C，有
card(A∪B∪C)
=card(A)＋card(B)+card(C)－
card(A∩B)－ card(B∩C)－ card(C∩A)＋ card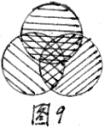
(A∩B∩C)
其道理可由图9看出来。
三、练习题
A组
一、选择题
(1．已知全集I={0,－1 ,－2 ,－3 ,－4}，集合M={0,1,－2}，N ={0,－3,－4}，则=
A.{0} B.{－3，－4} C.{－1，－2} D. φ
(2．设全集为R，集合M={x f(x)=0}，P={x g(x)=0}，S={x
h(x)=0}，则方程
的解集是（ ）
A. M∩P∩N B.M∩P
C.M∩P∩S
D.M∩P∩
(3．已知集合P、M满足P∩M={1，2}，P∪M={1，2，3，4，5}，全集I=N，则(P∪M)∩(
)为（ ）
A.{1，2，3} B.{2，3，4} C.{3，4，5} D.{1，4，5}
(4．设I是全集，集合P、Q满足P∈Q，则下面结论中错误的是
A.P∪Q=Q
B.
C.
D.
(5．满足{1，2}∪M={1，2，3}的所有集合M有（ ）
A.1个 B.2个 C.3个 D. 4个
二、填空题
1、设A={梯形}，B={平行四边形}，C={矩形}，D={菱形}，E={正方形}，则(A∩B) ∪(B∩C)∪(D∪E)=
.
2、设x,y∈R，集合A={(x,y)4x－y－3=0},B={(x,y)2x－3y＋11=0} , 则A∩B= .
3、全集I={1，2，3，4}，子集A和B满足： 
={1}，A∩B={3}， 
={2}，则A=
。
4、集合A={1，x2}，且
={1，3，x}，则实数x的取值范围是
。
5、某班48名学生中，有13人爱打篮球又爱唱歌，有29人不爱唱歌，有16人不爱打篮球。则不爱打篮球
又不爱唱歌的学生数为 。
答案：
一、选择题
1—5 B，D，C，D，D
二、填空题
1、D
2、{(2 , 5)}
3、{3 , 4}
4、{0 , －
, }
5、10
B组
一、选择题
1．集合{1，2，3}的子集共有（ ）
A．7个 B．8个 C．6个 D．5个
2．下列命题或记法中正确的是（ ）
A．R+∈R
B．Z-
{xx
0,x∈Z}
C．空集是任何集合的真子集 D．
3．同时满足{1}
A
{1，2，3，4，5}，且A中所有元素之和为奇数的集合A的个数是（ ）
A．5 B．6 C．7 D．8
4．设A={x1<x<2},B={xx<a},若AB，则a的取值范围是（ ）
A．
B．
C．
D．
5．六个关系式：（1）{a,b}={b,a};(2){a,b}{b,a}；（3）
；（4）{0}=
；（5）{0}；
（6）0∈{0}。其中正确的个数为（ ）
A．6个 B．5个 C．4个 D．3个及3个以下
6．集合M={xx=3k-2，k∈Z}，P={yy=3l+1,l∈Z}，S={yy=6m+1,m∈Z}之间的关系是（ ）
A．SPM B．S=PM C．SP=M D．S
P=M
二、填空题
7．已知集合P={xx2=1},集合Q={xax=1},若QP，那么a的值是________。
8．设S={xx是至少有一组对边平行的四边形}，A={xx是平行四边形}，则CsA=________.
9．求满足条件{xx2+1=0,x∈R}的集合M的个数。
答案：
一、1．B 2．D 3．C 4．A 5．C 6．C
二、7．0、或—1 8．{xx是梯形}
9．{xx2+1=0,x∈R}=
，又{xx2-1=0,x∈R}={-1,1},其非空子集为{-1}，{1}，{-1，1}。
所以满足条件{xx2+1=0,x∈R}M{xx2-1=0}的集合M共3个.