含绝对值的不等式解法
一、学习要求：
1、掌握x＜a，x＞a型不等式解法。
2、能将含绝对值的不等式化归为x＜a，x＞a型的不等式。
3、掌握实数子集的简洁表示法──区间。
二、例题：
第一阶梯
例1、总结一下初中学过的不等式的基本性质。
答案：
不等式的基本性质：
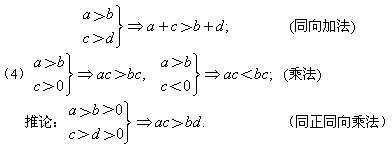
说明：
1、上面每条性质后面用括号注明性质的名称，其用意是帮助你加深理解和记忆。这些性质到了高中
二年级还要系统学习，如果在高一你就熟练地掌握了不等式的基本性质，那么你的整个数学学习
将少犯错误。
2、上面使用了现代语言符号"
"、"
"，后面将在"充要条件"一节中学习它，现在""译成"推出"，
而"AB"表示"AB，且BA"，即""译成"等价"较早地熟练使用这些符号，将推进你的数学学习。
例2、写出实数绝对值的定义。
答案：
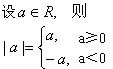
说明：
绝对值的定义是用分类法给出的，这种分类是以"0"划分的，所以叫做"零点划分"。利用绝对值的定
义可以脱去绝对值，同时"零点划分"是今后解决含绝对值的问题的一个基本分类方法。
例3、写出不等式x＜a，x＞a（a＞0）的同解定理，并把解表示在数轴上。
提示：
x的几何意义表示数轴上的点x到原点的距离，利用绝对值的几何意义，直接得到不等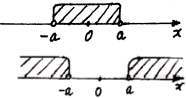
式的解。
答案：
不等式x＜a，x＞a（a＞0）的同解定理是
（Ⅰ）x＜a－a＜x＜a；
（Ⅱ）x＞ax＜－a，或x＞a。
说明：
1、同解定理（Ⅰ）和（Ⅱ）要利用绝对值的几何意义记熟。
2、应用同解定理（Ⅰ）和（Ⅱ）解ax+b＜c，ax+b＞c（c＞0）型不等式：
设ax+b=y，则这两个不等式化为
y＜c，y＞c
再应用同解定理可解。这个方法叫做换元法。
例4、试用集合的描述法给下列区间下定义：
[a,b]，(a,b)，[a,b]，(a,∞)，(－∞,+ ∞)
答案：
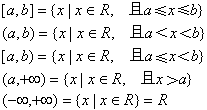
说明：
区间是表示实数子集的简洁方法，而不等式的解集都是实数的子集，因此，我们提前学习区间。例如
不等式x＜a，x＞a（a＞0）的解集可用区间分别表示为
（－a，a），（－∞，－a）∪（a，+∞）
因为区间是集合，所以对于区间可使用子、交、并、补等符号。各学校都在讲函数时讲授区间，因此，
很多同学不敢用简洁的区间取代集合的大括号表示法。
[a,b]叫闭区间，（a,b）叫开区间；
[a,b]，(a,b)叫半开半闭区间。
只要你记住含端点用"方括"，不含端点用"圆括"。
第二阶梯：
例1、解不等式ax＞b
提示：
对a进行分类讨论，分情况给出解集。
答案：
说明：
今后很多不等式都化归为不等式ax＞b，因此，遇到字母系数，不要忘记分类讨论。
例2、如果a＞b＞0，那么下列各式中错误的不等式是（
）
A、
B、ad＞bd
C、a－c＞b－c
D、c－a＜c－b
提示：
利用不等式性质
答案：
例3、解不等式
答案：
例4、等式1≤│2x-3│＜7
答案：
说明：
1、解不等式的过程必须步步等价，因此求解过程的表述用"即"或"等价"的语言，本例的表述用了
""，这是非常简明的，你应从此学会运用""。解不等式不可以用""（推出），这与"证明"
或解方程不同。
2、相连不等式a≤b＜c等价于不等式组
，而不等价于a≤b，或b＜c。这一点在本例求解开始时
要特别注意。
第三阶梯：
例1、解关于x的不等式：a(x－1)＞x－1
答案：
原不等式等价于
(a－1)x＞a－1
当a＞1时，则a－1＞0，解为x＞1；
当a＜1时，则a－1＜0，解为x＜1；
当a=1时，则a－1=0，0·x＞0无解。
综上，原不等式的解集：当a＞1时为（1，+∞）；当a＜1时为（－∞，1）；当a=1时为φ。
说明：
含字母的不等式的讨论问题始终是不等式的难点。
例2、解不等式│x+2│+│x-2│＞4
提示：
思路一：零点划分法。
思路二：数形结合法──利用绝对值的几何意义。
答案：
【解法一】 │x+2│+│x-2│＞4
由x+2=0得分点x1=－2，x－2=0得分点x2=2，于是分三种情况：
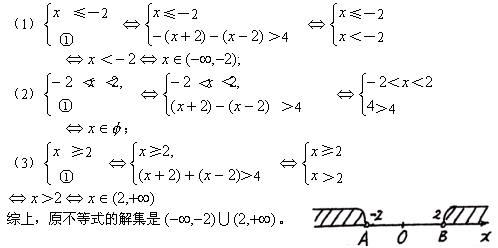
设－2，2在数轴上的对应点为A，B，如图：
不等式│x+2│+│x-2│＞4的解集，表示数轴上与A，B两点距离之和大于4的点集，又由图可知，数
轴上与A，B两点距离之和等于4的点集是线段AB（包括端点A、B），所以与A，B两点距离之和大于4的点在
线段AB的两侧延长线上（不包括端点A、B）。
∴原不等式的解集是
。
说明：
解法一──零点划分法是解决绝对值问题的通法，虽然有时麻烦，但非常清晰、好用，必须掌握它。
解法二是数形结合法，比解法一简捷，能直观地看到结果。这忠告你：要养成从数、形两个方面去思考的
习惯，提高数形结合的思维能力。
三、练习题
选择题
(1．如果a＜b，那么下列各式中错误的是（ ）
A.2a＜3b
B.a+1＜b+1
C.a－2＜b－2
D.－2a＞－2b
(2．不等式x－2＞3的解集是（ ）
A.{x│x＜5}
B.{x│-1＜x＜5}
C.{x│x＜-1}
D.{x│x＜-1，或x＜5＝
(3．已知a＞1, 则不等式│x+b│+a＞1的解集是（ ）
A.{x│b+a-1＜x＜b-a+1＝
B.{x│x＞b-a+1}
C.φ
D.R
(4．不等式0＜│x-1│≤2的解集是（ ）
A.[-1，3]
B.[-1，1）∪（1，3]
C.（1，3）
D.（-1，1）∪（1，3）
(5．设全集为R，A={xx＞6，或x＜－1}，B={xx－5＜a}其中a是常数，且11∈B ，则（ ）
A.
B.
C.
D.
二、填空题
1、当a＜2时，不等式ax＞2x的解集是
2、1-3x≤2的解集是
3、
的解集是 。
4、x+1＞x-3的解集是 。
5、2≤3x-2＜8（x∈Z）的解集是 。
答案：
一、1----5 A，D，D，B，C
二、1、（-∞，0）
2、
3、
4、（1，+∞）
5、{－1，0，2，3}