高考函数
一）选择题
1 (2004. 天津卷)若函数
在区间
上的最大值是最小值的3倍，则
=(A)
(A)
(B)
(C)
(D)
2. （2004.江苏）若函数
的图象过两点(-1，0)和(0，1)，则
( A )
(A)a=2,b=2 (B)a=,b=2 (C)a=2,b=1 (D)a=,b=
3. （2004.江苏）设k>1，f(x)=k(x-1)(x∈R) . 在平面直角坐标系xOy中，函数y=f(x)的图象与x轴交于A点，它的反函数y=f -1(x)的图象与y轴交于B点，并且这两个函数的图象交于P点. 已知四边形OAPB的面积是3，则k等于 ( B )
(A)3 (B) (C) (D)
4．(2004.全国理)已知函数
（ B ）
A．b B．－b C．
D．－
5．(2004.全国理)函数
的反函数是 （ B ）
A．y=x2－2x+2(x<1) B．y=x2－2x+2(x≥1)
C．y=x2－2x (x<1) D．y=x2－2x (x≥1)
6、（2004.上海理）若函数y=f(x)的图象可由函数y=lg(x+1)的图象绕坐标原点O逆时针旋转
得到,则
f(x)=( A )
(A) 10-x-1. (B) 10x-1. (C) 1-10-x. (D) 1-10x.
7、（2004. 上海卷文科)若函数y=f(x)的图象与函数y=lg(x+1)的图象关于直线x-y=0对称,则
f(x)=( A )
(A)10x-1. (B) 1-10x. (C) 1-10-x. (D) 10-x-1.
8．（2004.湖北理）已知
的解析式可取为 （ C ）
A．
B．
C．
D．
9．（2004.湖北理）函数
上的最大值和最小值之和为a，则a的值为（ B ）
A． B． C．2 D．4
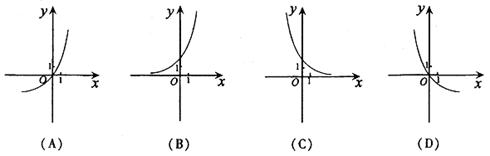
10．（2004. 福建理）已知函数y=log2x的反函数是y=f—1(x)，则函数y= f—1(1－x)的图象是 （ B ）
11 (2004. 天津卷)函数
的反函数是(D)
(A)
(B)
(C)
(D)
12．（2004. 福建理）定义在R上的偶函数f(x)满足f(x)=f(x+2)，当x∈[3，5]时，f(x)=2－x－4，则（ D ）
A．f(sin
)<f(cos)
B．f(sin1)>f(cos1)
C．f(cos
)<f(sin)
D．f(cos2)>f(sin2)
13．（2004. 重庆理）函数
的定义域是： （ D
）
A．
B．
C．
D．
14．（2004. 重庆理）一元二次方程
有一个正根和一个负根的充分不必要条件是： （ C
）
A．
B．
C．
D．
15．（2004. 辽宁卷）对于
，给出下列四个不等式D
①
②
③
④
其中成立的是
A．①与③ B．①与④ C．②与③ D．②与④
(16) (2004. 天津卷)定义在R上的函数
既是偶函数又是周期函数。若的最小正周期是
，且当
时，
，则
的值为(D)
(A)
(B) (C)
(D)
17．（2004.湖南理）设
是函数
的反函数，若
，则
的值为 （ B ）
A．1 B．2 C．3 D．
18．（2004.湖南理）设函数
则关于x的方程
解的个数为 （ C ）
A．1 B．2 C．3 D．4
2004. 四川理）函数y=-ex的图象( D )
A 与y=ex的图象关于y轴对称. B 与y=ex的图象关于坐标原点对称.
C 与y=e-x的图象关于y轴对称. D 与y=e-x的图象关于坐标原点对称.
19．（2004.湖南理）设
分别是定义在R上的奇函数和偶函数，当
时，
且
则不等式
的解集是 （ D ）
A．
B．
C．
D．
20、（2004. 人教版理科）函数
的定义域为（ ）
A、
B、
C、
D、
二）填空题
21．（04. 上海春季高考）方程
的解
__________.2
22．（04. 上海春季高考）已知函数
，则方程
的解__________.1
(x≠0)，
23．（2004. 福建理）设函数f(x)= a (x=0). 在x=0处连续，则实数a的值为
1/2 .
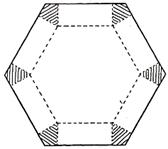
24．（2004. 福建理）如图1，将边长为1的正六边形铁皮的六个角各
切去一个全等的四边形，再沿虚线折起，做成一
个无盖的正六棱柱容器.当这个正六棱柱容器的
底面边长为 2/3 时，其容积最大.
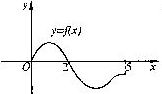
25、（2004.上海理）设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时, f(x)的图象如右图,则不等式f(x)<0的解是 (－2,0)∪(2,5] .
26、（2004.上海理）若函数f(x)=a
在[0,+∞)上为增函数,则实数a、b的取值范围是 a>0且b≤0 .
27、（2004. 人教版理科）已知函数
是奇函数，当
时，
，设
的反函数是
，则
.
28、（2004. 人教版理科）设函数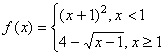
，则使得
的自变量
的取值范围为（ ）
A、
B、
C、
D、
29.二次函数y=ax2+bx+c(x∈R)的部分对应值如下表：
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
则不等式ax2+bx+c>0的解集是_______________________.
或
21．（2004. 福建理）（本小题满分14分）
已知f(x)=
(x∈R)在区间[－1，1]上是增函数.
（Ⅰ）求实数a的值组成的集合A；
（Ⅱ）设关于x的方程f(x)=
的两个非零实根为x1、x2.试问：是否存在实数m，使得不等式m2+tm+1≥x1－x2对任意a∈A及t∈[－1，1]恒成立？若存在，求m的取值范围；若不存在，请说明理由.
21.本小题主要考查函数的单调性，导数的应用和不等式等有关知识，考查数形结合及分类讨论思想和灵活运用数学知识分析问题和解决问题的能力.满分14分.
解：（Ⅰ）f＇(x)=
= 
，
∵f(x)在[－1，1]上是增函数，
∴f＇(x)≥0对x∈[－1，1]恒成立，
即x2－ax－2≤0对x∈[－1，1]恒成立. ①
设
(x)=x2－ax－2，
方法一：
(1)=1－a－2≤0，
① 
－1≤a≤1，
(－1)=1+a－2≤0.
∵对x∈[－1，1]，f(x)是连续函数，且只有当a=1时，f＇(-1)=0以及当a=－1时，f＇(1)=0
∴A={a－1≤a≤1}. 方法二：
≥0，
<0，
①
或
(－1)=1+a－2≤0
(1)=1－a－2≤0
0≤a≤1
或 －1≤a≤0
－1≤a≤1.
∵对x∈[－1，1]，f(x)是连续函数，且只有当a=1时，f＇(－1)=0以及当a=-1时，f＇(1)=0
∴A={a－1≤a≤1}.
（Ⅱ）由=，得x2－ax－2=0， ∵△=a2+8>0
∴x1，x2是方程x2－ax－2=0的两非零实根，
x1+x2=a，
∴
从而x1－x2=
=
.
x1x2=－2，
∵－1≤a≤1，∴x1-x2=≤3.
要使不等式m2+tm+1≥x1－x2对任意a∈A及t∈[－1，1]恒成立，
当且仅当m2+tm+1≥3对任意t∈[－1，1]恒成立，
即m2+tm－2≥0对任意t∈[－1，1]恒成立. ②
设g(t)=m2+tm－2=mt+(m2－2)，
方法一：
g(－1)=m2－m－2≥0，
②
g(1)=m2+m－2≥0，
m≥2或m≤－2.
所以，存在实数m，使不等式m2+tm+1≥x1－x2对任意a∈A及t∈[－1，1]恒成立，其取值范围是{mm≥2，或m≤－2}.
方法二：
当m=0时，②显然不成立；
当m≠0时，
m>0，
m<0，
②
或
g(－1)=m2－m－2≥0 g(1)=m2+m－2≥0
m≥2或m≤－2.
所以，存在实数m，使不等式m2+tm+1≥x1－x2对任意a∈A及t∈[-1，1]恒成立，其取值范围是{mm≥2，或m≤－2}.
1. （04. 上海春季高考）(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分，第3小题满分6分.
已知函数
，
（
为正常数），且函数
与
的图象在
轴上的截距相等。
（1）求的值；
（2）求函数
的单调递增区间；
（3）若
为正整数，证明：
.
21.(1)由题意，
，
又
，所以
。
(2)
当
时，
，它在
上单调递增；
当
时，
，它在
上单调递增。
(3)设
，考查数列
的变化规律：
解不等式
，由
，上式化为
解得
，因
得
，于是
，而
所以
。
22．（2004. 辽宁卷）（本小题满分12分）
已知函数
.
（1）求函数
的反函数
的导数
（2）假设对任意
成立，求实
数m的取值范围.
所以
都是增函数.
因此当
时，
的最大值为
的最小值为
而不等式②成立当且仅当
即
，于是得 
………………12分
解法二：由
得
设
于是原不等式对于
恒成立等价于
③…7分
由
，注意到
故有
，从而可
均在
上单调递增，因此不等式③成立当且仅当
即 ………………12分
22.（2004.江苏）已知函数
满足下列条件：对任意的实数x1，x2都有
和
，其中
是大于0的常数.设实数a0，a，b满足
和
(Ⅰ)证明
，并且不存在
，使得
；
(Ⅱ)证明
；
(Ⅲ)证明
.
22、解：（1）不妨设
，由
可知
，
是R上的增函数
不存在
，使得
又
（2）要证：
即证：
不妨设
，
由
得
，
即
，
则
（1）
由
得
即
，
则
（2）
由（1）（2）可得
（3）
,
又由（2）中结论
