高级中学第一学期单元测试三
高三数学（函数2）
班级
姓名
学号
一、填空：
1． 方程
的解是
。
2． 若函数
的反函数
。
3． 计算
=
。
4． 函数
的最大值为
。
5． 函数
的值域为 。
6． 函数
在区间(-6,
)上单调递减，则实数的取值范围是
。
7． 设f(x)为奇函数，且当x＞0时f(x)＝x(1-x)，则当x＜0时，f(x)＝ 。
8．若函数
且
在[1，2]上的最大值比最小值大
，则的值为 。
9．设函数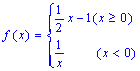
,若
，则实数的取值范围是
。
10．已知函数
的图像与x轴有交点，则实数的取值范围
。
二、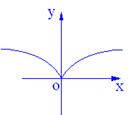
选择题：
11．如图,是下列某个函数所对应的图像，则这个函数是 （ ）
(A)
(B)
(C)
(D)
12．函数
的图像（ ）
(A)关于x 轴对称 (B) 关于y轴对称
(C) 关于原点对称 (D) 关于直线y=x对称
13．函数
,若函数g(x)的图像与
的图像关于y=x对称，那么g(2)的值等于
( )
(A)-1 (B)-2
(C)
(D)
14．已知函数y=f(x)（x∈R）满足f(x+1)=f(x—1)，且x∈[—1，1]时，f(x)=x2，则y=f(x)与y=log5x的图象的交点个数为 （ ）
(A)2 (B)3 (C)4 (D)5
三、解答题：
15．已知函数y =
的定义域为R，
(1)求实数的取值范围；
(2)当
变化时，若y的最小值为
，求的值域。
16．已知函数f(x)满足条件
。
(1)求函数f(x)的表达式；(2)求函数f(x)的定义域；(3)判断奇偶性与实数之间的关系。
17．设函数
（1）证明
在
上是减函数；（2）当
时，求的最小值。
18．运货卡车以每小时千米的速度匀速行驶130千米，按交通法规限制
（单位：千米/小时）．假设汽油的价格是每升2元，而汽车每小时耗油
升，司机的工资是每小时14元．
（Ⅰ）求这次行车总费用
关于的表达式；
（Ⅱ）当为何值时，这次行车的总费用最低，并求出最低费用的值．（精确到小数点后两位）
参考答案：
1．
2. 
3. 
4. 
5. 
6. 
7. 
8. 
或 9. 
10. 
11. C 12. C 13. B 14.C
15.(1)
;(2)
.
16. 
;(2)当
时,
,当
时,
;(3)当
时,
,
为奇函数;当
时,函数为非奇非偶函数.
17.(1)略;(2)当
时,
;当
时,
;当
时,
.
18.(1)
;(2)当
时,的值最小为
元。