函数 (高考题)
一、选择题:
1、已知y=loga(2-ax)在[0,1]上是x的减函数,则a的取值范围是( ) (1995年全国)
A、(0,1) B(1,2) C(0,2) D[2,+∞]
2、当0<a<b<1时,下列不等式中正确的是( ) (1995年上海)
A、(1-a)1/b>(1-a)b B、(1+a)a>(1+b)b C、(1-a)b>(1-a)b/2 D、(1-a)a>(1-b)b
3、设函数y=f (x)定义在实数集上,则函数y=f (x -1)与y=f (1- x)的图象图象关于( ) (1997年全国)
A、直线y=0对称 B、直线x=0对称 C、直线y=1对称 D、直线x=1对称
4、三个数60.7,0.76,log0.76的大小顺序是( ) (1997年上海)
A、0.76<log0.76<60.7 B、0.76<60.7<log0.76
C、log0.76<60.7<0.76 D、log0.76<0.76<60.7
5、若函数y=f (x)的反函数是y=g(x),f (a)=b,ab≠0,则g(b)等于( ) (1999年全国) A、a B、a-1 C、b D、b-1
![]() 6、已知函数f
(x)=ax3+bx2+cx+d的图象如图所示,
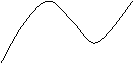
6、已知函数f
(x)=ax3+bx2+cx+d的图象如图所示,
![]()
![]()
![]()
![]() 则( )
(2000年安徽
春)
则( )
(2000年安徽
春)
![]() A、b∈(-∞,0) B、b∈(0,1)
0 1 2
A、b∈(-∞,0) B、b∈(0,1)
0 1 2
C、b∈(1,2) D、b∈(2,+ ∞)
7、已知f(x6)=log2x,那么f(8)等于( )(2001年北京 春)
A、4/3 B、8 C、18 D、1/2
8、若实数a、b满足a + b=2,则3a + 3b 的最小值是( )(2001年北京 春)
A、18 B、6
C、![]() D、
D、![]()
9、函数y=1+3x-x3有( )(2001年 天津)
A、极小值-1,极大值1 B、极小值-2,极大值3
C、极小值-2,极大值2 D、极小值-1,极大值3
10、函数![]() ( ) (2002年 广东)
( ) (2002年 广东)
A、在(-1,+∞)内单调递增 B、在(-1,+∞)内单调递减
C、在(1,+∞)内单调递增 D、在(1,+∞)内单调递减
二、填空题:
11、设f(x)=x2(2-x),则f(x)的单调递增区间是 ;(1997年上海)
12、某工程的工序流程图如下(工时单位:天),则工程总时数为
天;(1998 年上海)
年上海)
13、若正数a,b满足ab=a+b+3,则
ab的取值范围是 ;(1999年全国)
14、设函数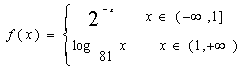 ,则满足f(x)=1/4的x值为
。(2001年 上海)
,则满足f(x)=1/4的x值为
。(2001年 上海)
15、已知函数![]() ,那么
,那么![]() =
;(2002年 全国)
=
;(2002年 全国)
16、函数![]() 的图象与其反函数图象的交点坐标为 。(2002年
全国)
的图象与其反函数图象的交点坐标为 。(2002年
全国)
三、解答题:
17、设a>0,f(x)=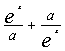 是R上的偶函数。(2001年
天津)
是R上的偶函数。(2001年
天津)
(1)求a的值; (2)证明f(x)在(0,+∞)上是增函数。
18、设a为实数,函数f(x)=x2+x-a+1,x∈R.(2002年 全国)
(1)讨论f(x)的奇偶性; (2)求f(x)的最小值。
19、对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点。已知函数f(x)=ax2+(b+1)x+(b-1)(a≠0)。(2002年 上海)
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动点,且A、B两点关于直线![]() 对称,求b的最小值。
对称,求b的最小值。