函数测试题
班级 姓名 得分 .
一、选择题：
1、函数y=
（a≤x≤b），则集合{(x,y) y=,a≤x≤b}∩{(x,y) x=0}中元素个数有……( )
(A)0个 (B) 1或者0个 (C)1个 (D) 1或者2个
2、函数=
的值域为……………………………………………………( )
(A)[－1，1] (B)（－∞，1] (C)[1，＋∞） (D)[3，＋∞）
3、函数y=满足
，则下列结论正确的是…………………………………（ ）
(A)y=
为偶函数
(B)y=
为偶函数
(C）y=为偶函数
（D）y=
为偶函数
4、函数y=
在区间[1，3]上是减函数，则实数a的取值范围是…………………………（ ）
(A)（－∞，
]
（B）（－∞，1] （C）[，
] （D）[，＋∞）
5、定义域为R的偶函数y=在[0，7]上为增函数，在[7，＋∞）上为减函数，
，则（ ）
(A)在[－7，0]上是增函数，最大值是6 (B) 在[－7，0]上是减函数，最大值是6
(C)在[－7，0]上是增函数，最小值是6 (D) 在[－7，0]上是减函数，最小值是6
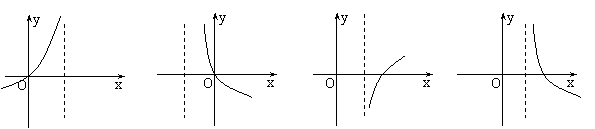6、函数=
，则函数y=
的图象大致是………………………………………（
）
(A) (B) (C) (D)
7、函数y=
的反函数为…………………………………………………………（ ）
(A)y=
(B) y=
(C) y=
(D) y=
8、函数=
的单调递增区间是…………………………………………………………（ ）
(A)（0，]
(B) （ 0，1]
(C)（0，＋∞） (D)[1，＋∞）
9、函数=
，则m、n的大小为…（ ）
(A)m<n (B)m=n (C) m>n (D)m、n大小不能确定
10、函数定义域为R，满足
时<0，则为……（ ）
(A)奇函数，增函数 (B) 偶函数，在（－∞，0）上增，在（0，＋∞）上减
(C)奇函数，减函数 (D)偶函数，在（－∞，0）上减，在（0，＋∞）上增
11、y=是R上偶函数，满足
，当2≤x≤3时，=x，则
=（ ）
(A)－2.5 (B) 2.5 (C) 5.5 (D) －5.5
12、国庆期间，某商场为了吸引顾客，实行“买100送20”活动，即顾客购满100元，就可以获得商场购物券20元，并且购物可以用现金也可以用购物券，如果你有680元现金，在活动期间到该商场购物，最多可以获得购物券累计……………………………………………………………（ ）
(A)120元 (B) 136元 (C)140元 (D)160元
二、填空题：
13、函数=
的反函数定义域为
。
14、函数=
的定义域为R，则实数k的取值范围为
。
15、函数满足：对任意
，都有
，并且当x1<x2时，
，试写出一个满足这些条件的函数=
。
16、下列四个命题：⑴
的图象关于原点对称；⑵
在R上是减函数；⑶=
的最小值为lg2；⑷将函数=
的图象左平移1个单位，再下平移一个单位后与函数=
的图象重合。其中正确命题的序号是
.
三、解答题：
17、函数=
。
⑴求其定义域；
⑵判断其奇偶性并证明你的结论；
⑶当a>1时，求使>0的x的范围。
18、已知是定义在R上并且以2为周期的函数，当x∈[0，2]时，=x－1。
⑴作出函数y=至少两个周期的图形；
⑵写出函数y=在区间[2k，2k＋1]（k∈Z）上的表达式，并且证明y=是偶函数。
19、某医药研究所开发新药，如果成人按照规定服用，根据检测，服药后每毫升血液中的含药量y与时间t之间近似民族如图曲线。
⑴写出服药后y与时间t之间的函数关系式；
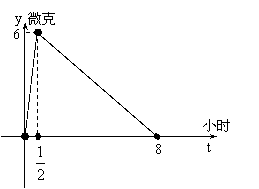⑵根据测定，每毫升血液含药量不少于4毫克时，治疗有效。假如某病人一天中第一次服药为7：00，问一天（12小时）中这样安排服药时间、次数，效果最佳？
20、函数对任意m、n∈R，都有
，并且当x>0时，>1。
⑴求证y=在R上为增函数；
⑵如果
，求
并解不等式