| 姓名 | 班级 | 学号 | 时间 | ||||
| 课题 | 函数的单调性 | 设计 |
| ||||
| 一、方法点拨: 1. 理解函数单调性的概念,并能判断一些简单函数的单调性。 2. 判断函数单调性的方法: (1)观察法 (2)分解法 (3)图像法。 (4)定义法 二、知能达标: 1如果函数f(x)=x A. 2.函数y= A.
3.已知函数 f(x)为偶函数,在(0,+ A 2 B 2或1 C 3 D 2或3 4当0 5. 偶函数f(x)是以4为周期的函数,f(x)在区间 6.已知函数f(x)=
| |||||||
| 7.已知函数f(x)= 8.设f(x)是定义在R上的增函数,F(x)=f(x)-f(a-x) (1) 用函数单调性的定义证明F(x)是R上的增函数;(2)证明函数y=F(x)的图像关于 点( 9.设f(x)是定义在R上的函数,且对任意实数x、y都有f(x+y)=f(x)+f(y)。求证:(1)f(x) 是奇函数。 (2)当x>0时,有f(x)>0,则f(x)在R上是增函数。 |
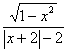 求证: (1)f(x)是奇函数 (2)f(x)在区间(0,1)上是减函数。
求证: (1)f(x)是奇函数 (2)f(x)在区间(0,1)上是减函数。