函数的单调性和奇偶性
一、学习目标
1.理解函数的单调性概念，能根据函数单调性定义证明函数在给定区间上的增减性。
2.会判定函数的单调性，会求单调区间。
3.准确掌握一次函数、二次函数的单调性。
4.解奇函数、偶函数的概念及图像物征，能判断某些函数的奇偶性；
二、例题分析
第一阶梯
[例1]什么叫函数f (x)在区间[a,b]上是增函数（减函数）？
[解]
设任意的x1,x2∈[a,b],当x1<x2时，都有f(x1)<f(x2),那么就说f(x)在区间[a,b]上是增函数。
设任意的x1，x2∈[a,b],当x1<x2时，都有f(x1)>f(x2)，都有f(x1)>f(x2)，那么就说f(x)在区间
[a,b] 上是减函数。
[评注]
1.f(x)在某个区间上是增函数或减函数，那么就说函数f(x)在这一区间具有（严格的）单调性，
这一区间叫做f(x)的单调区间。
2.函数的单调性相对于区间而言，这个区间当然是函数定义域的子集。
例如，
的定义域A=（－∞，0）∪（0，+∞）,那么，下列说法正确的是
（把正确说法的代号都填上）
①f(x)在其定义域A上是增函数
②f(x)是单调函数
③f(x)在区间（－∞，0）上是增函数
④f(x)在区间（0，+∞）上是减函数
⑤f(x)的单调增区间有（－∞，0），（0，+∞）
答：正确说法是③、⑤，其它说法都是错误的，我们着重论证说法①是错误的：设x1=1,x2=1,则x1,
x2∈A,但
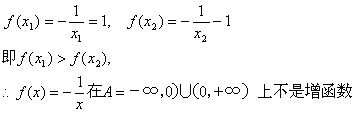
[例2]怎样根据函数单调性定义，证明函数的增减性？试举一例。
[解]根据单调性定义证明函数增减性的步骤是：
（1）设x1,x2:即设x1、x2是该区间上的任意二值，且x1<x2
（2）比较f(x1)和f(x2)的大小：通常采用作差法，即作差f(x1)-f(x2)，变形，定号。
（也可以用“作商”等其它比较法）
（3）作出结论：根据单调性定义，作出增函数或减函数的结论。
例：根据函数单调性定义证明
在区间（0，2]上是减函数。
证明：设0<x1<x2≤2，则
由
；
由
∴由①得，f(x1)－f(x2)>0，即f(x1)>f(x2)。
∴ 
在区间（0，2）上是减函数。
[例3]怎样判别函数的单调性？举例说明。
【解】目前应该学会判断单调性的三个判别法：
1、定义法：根据增函数、减函数的定义来判别。例如，判别函数
的单调性：
根据定义，先取x2>x1>0，作差
这里的△f是函数改变量f(x2)－f(x1)的记号。函数f(x)的单调性由△f的符号来确定，而△f的符号
来确定， △f的符号由因式x1x2—4来确定：显然x=2是分界点，当x1，x2∈（0，2）时，x1x2－4<0，从
而△f<0， 即f(x2)<f(x1)，所以f(x)在（0，2）上减函数；当x1，x2∈[2，+∞]时，x1x2－4>0，从而
△f>0，即f(x2)>f(x1)， 所以f(x)在[2，+∞]上是增函数。这就是“定义法”，我们根据增减性定义，求
得了：
函数
的单调区间：（0，2）是减区间，[2，+∞]是增区间。
2、图象法：在直角坐标系中，函数y=f(x)在某一区间上从左到右图象上升，则f(x)在该区间上是增函数；
相反，图象下降，则f(x)是减函数。简言为“升增降减”。例如求二次函数f(x)=－x2+4x+1的单调性。
因此f(x) 的图象是开口向下的抛物线，其最高的横坐标为2，在（－∞，2）上图象上升，在[2，+∞]上图
象下降， 所以f(x)的单调增区间是（－∞，2），单调减区间是[2，+∞]。
3、复合法：其判别法则是增函数的增函数是增函数；增函数的减函数是减函数；减函数的增函数是减函
数； 减函数的减函数是增函数。
简言为：增·增
增；增·减减；
减·增减；减·减增。
可类比乘法符号法则来记忆：
（+）·（+）=（+）；（+）·（－）=（－）；
（－）·（+）=（－）；（－）·（－）=（+）；
例如，求函数
的单调性。
解：先作复合映射
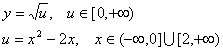
函数u=x2-2x在（－∞，0）上是减函数，且u∈[0，+∞]；而函数
在[0，+∞]上是增函数，
因为减函数的增函数是减函数，所以函数在（－∞，0]上是减函数。
同理，可得函数在[2，+∞]上是增函数。
【评注】
函数单调性的主要问题是求函数的单调区间和增减性。上面指出的三个判别法──定义法、图象法和
复合法 就是求单调递增区间或递减区间的基本方法。
第二阶梯
[例4]根据函数单调性定义，证明函数
上是增函数。
【证明】设x2>x1≥2，则
[例5]根据函数单调性定义，证明函数
在定义域上是减函数。
【证明】由3－x≥0得x≤3，
∴函数f(x)的定义域是（－∞，3]
设
，则
……①
∵x1<x2≤3，
∴
，
∴由①得 
∴ 在其定义域（－∞，3）上是减函数。
【评注】
要注意严格按“定义法”证明的三步骤进行：在第一步中，应设，如果设成“x1<x2”或设
成“x1<x2<3”都是错误的。在第二步中，作差f(x1)－f(x2) ，要化成容易“定号”的形式，本题在①处
用 了“分子有理化”的技巧！应注意学会：
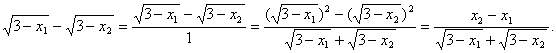（这里是慢镜头）。
在第三步中，一定要根据定义作出明确的结论。
[例6]试总结下列函数的单调性：
（1）
（2）
【解】
（1）当k>0时，f(x)在（－∞，+∞）上是增函数；当k<0时，f(x)在（－∞，+∞）上是减函数。
（2）当a>0，g(x)在（－∞，
）上是减函数，在[ ，+∞]上是增函数。
第三阶段
[例7]求下列函数的单调区间，并指出增减性（不要求证明）：
（1） 
； （2） 
。
【探路】化归为基本函数，用复合法解（1）；用图象法解（2）。
【解】
（1）函数的定义域是
，根据函数
和
的单调性，得函数
的单调递增区间是： 。 的单调递增区间是： 。
（2）函数
的定义域是 
。作出该函数的图象如图1中的实线。由图可知：
函数的单调递减区间是：
；单调递增区间是：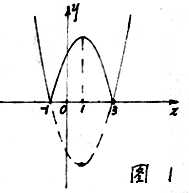
。
【评注】
求函数的单调区间有定义法、图象法、复合法，把复杂的函数化归为基 本
函数的性质和图象来解决。但要注意选择快法，如本例之（2）用图象法是
“快法”。其中画图只需画草图，一分钟即可画出。如用“复合法”解（2）
也可以成功，但很慢，且容易求错。
例8：已知函数
上是增函数，求实数a的取值范围。
【探路】
画出二次函数的草图，用二次函数的单调界点来列a的不等式。
【解】如草图2，抛物线顶点横坐标为
，函数是增函数的条件是
，
解得a的取值范围：a≤2。
[例9]根据函数单调性定义，证明函数
上是减函数。
【探路】
严格按照“根据定义证明单调性”的三个步骤来证明，特别注意难点是
的“定号”。
由于
，需证
恒为正数，于是想到配方：
但x1x2的符号不定，所以思路受阻，进而自我调节，产生各种思路：
思路一：分类讨论。
思路二：重新配方，看能否不分类就能确定符号。
【证法一】
任取x1<x2，则
其中 
的符号：
当x1x2≥0时，由x1<x2x1、x2中至少有一个非零
当x1x2<0时，由－x1x2>0
∴对任意的x1<x2，恒有
又由
∴
，
∴函数上是减函数。
【证法二】我们只证明：当x1<x2时，
。其余过程同证法一。
当且仅当
时，即x1=x2=0时，上式等于零。因为x1≠x2，所以恒成立。
【评注】
本题的证明方法一──分类法是排除解题受阻的一个通法。由于分类标准的不同，本题有许多证法，
请你发现几个不同的分类证法。
本题证明方法二是反分类，是本题最简捷的证法。
由本题可知，任意不等二实数a，b，恒有
。
[例10]判断函数
的奇偶性。
思路分析：
该题为分段函数，可分x<0和x>0两部分考察 
的关系，从而确定函数的奇偶性。
解：∵函数
的定义域
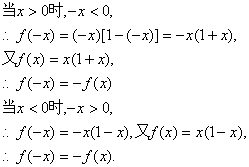
综上，对任意x∈(-∞,0)U(0,+∞)均有f(-x)=-f(x),所以函数f(x)为奇函数。
说明：本题关键要分段研究f(-x)与f(x)的关系。
[例11]证明函数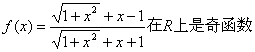
思路分析：
证明 
证明：函数的定义域为实数，且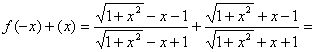
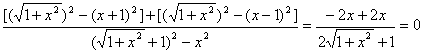
三、检测题
1.函数y=(2k+1)x-1在R上是减函数，则（ ）
A.
B.
C.
D.
2.下列函数中，在区间（0，1）上是增函数的是（ ）
A.
B.
C.
D.
3.下列说法中，正确的是（ ）
A.y=
是减函数
B.y= (－1，0)∪(0，1)上是减函数
C. y= (－∞，0)∪(0，+∞)上分别是减函数
D. y=
(0，+∞)上是减函数
4.函数f (x)=x2+2(a－1)x在区间（－∞，4）上是减函数，那么实数a的取值范围是（ ）
A.a≥3 B.a≤－3 C.a≤5 D.a=3
5.函数y=
的单调递减区间是
。
6.函数y=
的单调递减区间是
。
7.函数y=
在（0，1）上是增函数，则K的取值范围是
。
8.已知常数m和n满足mn<2,则函数
在区间（
，+∞）上的单调性为
9.函数
的单调递减区间是
。
10、若函数
的图像与函数
（ ）
A、是奇函数而不是偶函数。 B、是偶函数而不是奇函数。
C、既是奇函数也是偶函数。 D、不是奇函数也不是偶函数。
11、函数
（ ）
A、奇函数 B、偶函数 C、奇函数或偶函数 D、非奇非偶函数。
【答案】
1.D 2.A 3.C 4.B 5.(－∞，1)
6. [－
，+∞]
7.K<0
8.减函数
9. (－∞，0 )[1，3].
10、B
11、D