应用性问题预测
一、高考对应用题的考查已逐步走向成熟，大体上是3道左右的小题，一道大题，小题除了考查一些基本知识与能力外，近年的小题开始注意到问题及方法的新颖性，出现了非常规问题，提高了适应陌生情境的能力要求，大题的难度逐步趋向平稳
二、解应用题的一般思路可用下图表示：
三、解应用题的一般程序
（1）读：阅读理解文字表达的题意，分清条件和结论，理顺数量关系
（2）建：将文字语言转化成数学语言，利用数学知识，建立相应的数学模型
（3）解：求解数学模型，得到数学结论
（4）答：将数学方法得到的结论，还原为实际问题的意义
四、中学数学中常见的基本问题与数学模型
1、优选问题：常需建立不等式模型来解决
2、预测问题：通常设计为数列模型来解决
3、最值（极值）问题：通常设计成函数模型来解决
4、等量关系问题：常需建立方程（或方程组）模型来解决
5、测量问题：可设计成“图形模型”（包括三角形、空间图形、坐标系）来解决
6、计数问题：即排列、组合的应用问题
7、概率与统计问题：即概率与统计的应用问题
8、其它问题：如线性规划等问题
五、基础练习
1、某产品的总成本y（万元）与产量x（台）之间的函数关系式是y=3000+20x－0.1x2（0<x<240，x∈N），若每台产品的售价为25万元，则生产者不亏本时（销售收入不小于总成本）的最低产量是 （ ）
A.100台 B.120台 C.150台 D.180台
2、办公大楼共有15层，现每层（除13层外）派1人集中到第k层开会，当这14位参加会议的人员上、下楼梯所走路程的总和最少时，k的值为_______.
3、某品牌手机为了打开市场,促进销售,准备对其特定型号的产品降价,有四种降价方案:①先降价a%，再降价b%；②先降价
,再降价a%；③先降价，再降价；④一次性降价
%．其中
，则最终降价幅度最小的方案是（ ）
A．① B．② C．③ D．④
4、某校有6间不同的电脑室，每天晚上至少开放2间，欲求不同安排方案的种数，现有四位同学分别给出下列四个结果:
①
；②
；③
④
其中正确的结论是 （ ）
A. 仅有① B. 仅有②
C. ②和③ D. 仅有③
5、山坡水平面成30 角，坡面上有一条与山底坡脚的水平线成30 角的直线小路，某人沿小路上坡走了一段路后升高了100米，则此人行走的路程为 （ ）
A．300米
B．400米
C．200米
D．
米
6、我国发射的“神舟3号”宇宙飞船的运行轨道是以地球的中心
为一个焦点的椭圆，近地点
距地面为
千米，远地点
距地面为
千米，地球半径为
千米，则飞船运行轨道的短轴长为 （ ）
A. 
B. 
C. 
D. 
7、要将两种大小不同的钢板截成A、B、C三种规格，每张钢板可同时截得三种规格的小钢板的块数如下表：
| A规格 | B规格 | C规格 | |
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 2 | 3 |
今需A、B、C三种规格的成品各15、18、27块，所需两种规格的钢板的张数分别为、（、为整数），则+的最小值为 （ ）
A．10 B．11 C．12 D．13
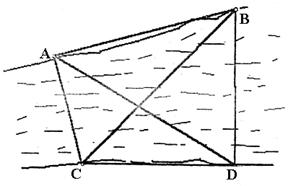
8、如图，要测量河对岸A、B两点间的距离，今沿河岸选取相距40米的C、D两点，测得∠ACB=60°，∠BCD=45°，∠ADB=60°，∠ADC=30°，则AB的距离是（ ）
A．20
B．20
C．20
D．40
|
六、典型例题
1、某人上午7时，乘摩托艇以匀速v海里/时（
）从A港出发到相距50海里的B港去，然后乘汽车以匀速w海里/时（
）从B港出向距300千米的C市驶去，要求在当天16：00时至21：00时这段时间到达C市。设汽车、摩托艇所需要的时间分别是x，y小时
（1）作图表示满足上述条件的x、y的范围
（2）如果已知所要的经费：p=100+3(5-x)+2(8-y)（元），那么v、w分别是多少时所要的经费最少？此时需花费多少元？
2、某届乒乓球比赛中，甲选手与乙选手在决赛中相遇，若每局比赛，甲选手获胜的概率为
，乙选手获胜的概率为
，每局比赛相互独立，比赛采用五局三胜制（即五局中先胜三局者为胜，比赛结束）
（1）求甲选手以总比分3：1获胜的概率
（2）求乙选手获胜的概率
3、某公司有价值a万元的一条流水线，要提高该流水线的生产能力，就要对其进行技术改造，改造就要提高产品附加值。假设附加值y万元与技术改造投入x万元之间的关系满足：①y与a-x和x和万元乘积成正比；②
时，
；③
其中t为常数，且
（1）设y=f(x)，求出f(x)的表达式，并求出y=f(x)的定义域
（2）求出附加值y的最大值，并求出此时的技术改造投入的x的值
4、一位救生员站在边长为100米的正方形游泳池ABCD的 A处（如图），发现C处有一位溺水者．他跑到E处后，马上跳水沿直线EC游到C处，已知救生员跑步的速度为米
／分，游泳的速度为
米／分．
试问：救生员选择在何处入水才能最快到达C处，所用的最短时间是多少？
5、现有流量均为300
的两条河流A、B会合于某处后，不断混合，它们的含沙量分别为2
和0.2．假设从汇合处开始，沿岸设有若干个观测点，两股水流在流经相邻两个观测点的过程中，其混合效果相当于两股水流在1秒钟内交换100
的水量，即从A股流入B股100水，经混合后，又从B股流入A股100水并混合．问：从第几个观测点开始，两股河水的含沙量之差小于0.01（不考虑泥沙沉淀）？
6、这是一个计算机程序的操作说明：
（1）初始值为
；
（2）
（将当前
的值赋予新的）；
（3）
（将当前
的值赋予新的
）；
（4）
（将当前
的值赋予新的
）；
（5）
（将当前
的值赋予新的
）；
（6）如果
，则执行语句（7），否则回语句（2）继续进行；
（7）打印
；
（8）程序终止．
由语句（7）打印出的数值为_____________，_____________ ．
请写出计算过程：
7、一根水平放置的长方体形枕木的安全负荷与它的宽度a成正比，与它的厚度d的平方成正比，与它的长度l的平方成反比．
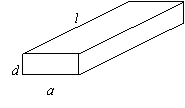（Ⅰ）将此枕木翻转90°（即宽度变为了厚度），枕木
的安全负荷变大吗？为什么？
（Ⅱ）现有一根横断面为半圆（半圆的半径为R）的木
材，用它来截取成长方体形的枕木，木材长度即为
枕木规定的长度，问如何截取，可使安全负荷最大？
8、设有半径为3km的圆形村落，A、B两人同时从村落中心出发，A向东而B向北前进，A出村后不久，改变前进方向，斜着沿切于村落周界的方向前进，后来恰好与B相遇。设A、B两人的速度都一定，其比为3：1，问A、B两人在何处相遇？
七、巩固练习
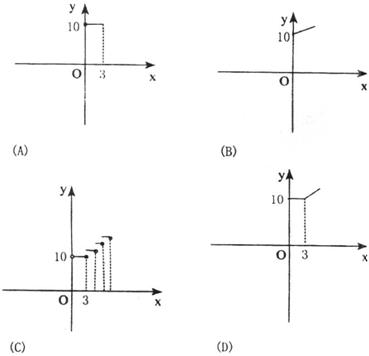
1、某城市出租车起步价为10元，最长可租乘3km（不含3km），以后每1km价为1．6元(不足1km，按1km计费)，若出租车行驶在不需等待的公路上，出租车的费用y(元)与行驶的里程x(km)之间的函数象大致为 （ ）
2、某农贸市场出售西红柿，当价格上涨时，供给量相应增加，而需求量相应减少，具体调查结果如下表：
表1 市场供给量
| 单价 （元/kg） | 2 | 2.4 | 2.8 | 3.2 | 3.6 | 4 |
| 供给量 （1000kg） | 50 | 60 | 70 | 75 | 80 | 90 |
表2 市场需求量
| 单价 （元/kg） | 4 | 3.4 | 2.9 | 2.6 | 2.3 | 2 |
| 需求量 （1000kg） | 50 | 60 | 65 | 70 | 75 | 80 |
根据以上提供的信息，市场供需平衡点（即供给量和需求量相等时的单价）应在区间（ ）
A.（2.3，2.6）内 B．（2.4，2.6）内 C．（2.6，2.8）内 D．（2.8，2.9）内
3、袋中有3个5分硬币，3个2分硬币和4个1分硬币，从中任取3个，总数超过8分的概率是_________.
4、某学生计划有不超过10元的钱购买单价分别为0.5元、0.6元的铅笔和练习本.根据需要，铅笔至少买7支，练习本至少买6本，则不同的选购方式共有
5、有一个各条棱长约为a的正四棱锥，现用一张正方形包装纸将其完全包住，不能裁剪，可以折叠．那么包装纸的最小边长为（ ）
A．
B．
C．
D．
6、某航空公司经营A、B、C、D这四城市之间的客运业务．它的部分机票价格如下：A—B 为2000元，A—C为1600元；A—D为2500元；B—C为1200元；C—D为900元．若这家公司规定的机票价格与往返城市间的直线距离成正比，则B—D的机票价格为（ ）（注：计算时视A、B、C、D四城市位于同一平面内）
A．1000元 B．1200元 C．1400元 D．1500元
7、用砖砌墙，第一层（底层）用去了全部砖块的一半多一块，第二层用去了剩下的一半多一块，…，依次类推，每一层都用去了上层剩下的砖块的一半多一块，如果到第九层恰好砖块用完，那么一共用了_______块砖．
8、如图，两条道路OA、OB相交成
角，在道路OA上有一盏路灯P，
米，若该灯的有效照明半径是
米，则道路OB上被路灯有效
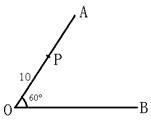照明的路段长度是
米。