高三数学综合练习D卷
一、选择题:本大题12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合A、B,全集∪,给出下列四个命题
⑴若![]() ,则
,则![]() ; ⑵若
; ⑵若![]() ,则
,则![]() ;
;
⑶若![]() ,则
,则![]() ; ⑷若
; ⑷若![]() ,则
,则![]()
则上述正确命题的个数为
A.1 B.2 C.3 D.4
2.设非零向量![]() 、
、![]() 、
、![]() ,若
,若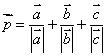 ,那么
,那么![]() 的取值范围为
的取值范围为
A.[0,1] B.[0,2] C.[0,3] D.[1,2]
3.设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,当
,当![]() 、
、![]() 变化时,若
变化时,若![]()
![]()
![]() 是一个定值,那么下列各数中也为定值的是
是一个定值,那么下列各数中也为定值的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.设![]() ,
,![]() ,则满足条件
,则满足条件![]() ,
,![]() 的动点P的变化范围(图中阴影部分含边界)是
的动点P的变化范围(图中阴影部分含边界)是
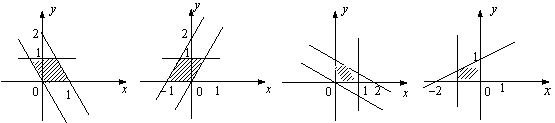 |
A B C D
5.在斜三角形ABC中,![]() 且
且![]() ,则∠A的值为
,则∠A的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.设两个非零向量![]() 不共线,若
不共线,若![]() 与
与![]() 也不共线,则实数k的取值范围为
也不共线,则实数k的取值范围为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.设A、B、C、D是半径为2的球面上四个不同的点,且满足![]() ,
,![]() ,
,
![]() ,则
,则![]() 的最大值为
的最大值为
A.16 B.8 C.4 D.2
8.由方程![]() 确定的函数
确定的函数![]() 在R上是
在R上是
A.奇函数 B.偶函数 C.增函数 D.减函数
9.已知函数![]() 在
在![]() 时有极值,其图象在点
时有极值,其图象在点![]() 处的切线与直线
处的切线与直线![]() 平行,则函数
平行,则函数![]() 的单调减区间为
的单调减区间为
A.(-∞,0) B.(0,2)
C.(2,+∞) D.(-∞,+∞)
10.定义在R上的函数![]() 对任意的x都有
对任意的x都有![]() 和
和![]() 且
且![]() ,则
,则![]() 的值为
的值为
A.2002 B.2003 C.2004 D.2005
11.分别把写有0,1,2,3,4数字的四张纸片放入一盒中,每次取一张记数字为m,放回后再取一张记数字为n,设P(m,n)为平面中的点,则点![]() 的概率为
的概率为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.下列三图中的多边形均为正多边形,M,N是所在边的中点,双曲线均以图中的F1,F2为焦点,设图示①②③中的双曲线的离心率分别为e1,e2,e3.
![]()
![]()


![]()
① ② ③
则e1、e2、e3的大小关系为
A.e1>e2>e3 B.e1<e2<e3 C.e2= e3 <e1 D.e1= e3>e2
二、填空题:本大题共4小题,每小题4分,共16分.
13.在![]() 的展开式中,含
的展开式中,含![]() 的系数为
.
的系数为
.
14.若![]() ,且
,且![]() ,
,![]() ,则
,则![]() =
.
=
.
15.一个公司有N个员工,下设一些部门,现采用分层抽样方法从全体员工中抽取一个容量为n的样本(N是n的倍数),已知某部门被抽取m个员工,那么这个部门的员工数为 .
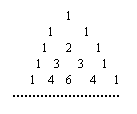 16.如右图,在杨辉三角形中,从上
16.如右图,在杨辉三角形中,从上
往下数共有n(n∈N*)行,在这些数中非1的
数字之和为
三、解答题:本大题共6小题,共74分.
17.(本题满分12分)
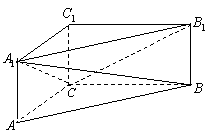
已知函数![]() 的图象关于直线
的图象关于直线![]() 对称,当
对称,当![]() 且
且![]() 时,求
时,求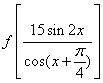 的值.
的值.
18.(本题满分12分)
某种工作元件有3个,它能正常工作的概率均为0.6,请设计成一个工作系统,使该系统正常工作的概率不低于0.7(要求画出系统图,并计算正常工作的概率)
19.(本题满分12分)
设函数![]() ,不等式
,不等式![]() 的解集为(-1,2)
的解集为(-1,2)
(Ⅰ)判断![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
 (Ⅱ)解不等式
(Ⅱ)解不等式![]() .
.
20.(本题满分12分)
如图,在直三棱柱ABC—A1B1C1中,AC=BC=![]() ,
,
AA1=1,∠ACB=90°.
(Ⅰ)求异面直线A1B与CB1所成角的大小;
(Ⅱ)问:在A1B1边上是否存在一点Q,使
得平面QBC与平面A1BC所成的角为30°,若存在,请求点Q的位置,若不存在,请说明理由.
21.(本题满分12分)
设![]() ,
,![]() 为直角坐标平面内x轴.y轴正方向上的单位向量,若
为直角坐标平面内x轴.y轴正方向上的单位向量,若![]() ,且
,且![]()
(Ⅰ)求动点M(x,y)的轨迹C的方程;
(Ⅱ)设曲线C上两点A.B,满足(1)直线AB过点(0,3),(2)若![]() ,则OAPB为矩形,试求AB方程.
,则OAPB为矩形,试求AB方程.
22.(本题满分14分)
直线![]() 与x轴.y 轴所围成区域内部(不包括边界)的整点个数为
与x轴.y 轴所围成区域内部(不包括边界)的整点个数为![]() ,所围成区域内部(包括边界)的整点个数为
,所围成区域内部(包括边界)的整点个数为![]() ,(整点就是横坐标,纵坐标都为整数的点)
,(整点就是横坐标,纵坐标都为整数的点)
(Ⅰ)求![]() 和
和![]() 的值;
的值;
(Ⅱ)求![]() 及
及![]() 的表达式;
的表达式;
(Ⅲ)对![]() 个整点用红.黄.蓝.白四色之一着色,其方法总
数为An,对
个整点用红.黄.蓝.白四色之一着色,其方法总
数为An,对![]() 个整点用红.黄.两色之一着色,其方法总数为Bn,试比较An与Bn的大小.
个整点用红.黄.两色之一着色,其方法总数为Bn,试比较An与Bn的大小.
参考答案
一、选择题
1.B 2.C 3.C 4.A 5.A 6.D
7.B 8.D 9.B 10.D 11.D 12.C
二、填空题
13.135 14.![]() 15.
15.![]() 16.
16.![]()
三、解答题
17.解:∵![]() ,得
,得![]() ……………2(分)
……………2(分)
又∵![]() ……4(分)
……4(分)
∴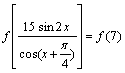 ………………………………8(分)
………………………………8(分)
由题意![]() 关于直线
关于直线![]() 对称
对称
∴![]() …………………………………………10(分)
…………………………………………10(分)
![]() 即
即![]() …………………12(分)
…………………12(分)
18.解法一:利用2个工作元件,系统图 …………6(分)
设工作系统为N,工作元件A.B独立
则系统正常工作的概率
![]() ……………………12(分)
……………………12(分)
(或![]() )
)

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 解法二:利用3个工作元件,系统图
…………6(分)
解法二:利用3个工作元件,系统图
…………6(分)
设工作系统为N,工作元件A=B.C独立
则系统正常工作的概率为
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ………………12(分)
………………12(分)
![]()
![]()
![]()
![]() 解法三:利用3个工作元件,系统图
………6(分)
解法三:利用3个工作元件,系统图
………6(分)
设工作系统为N,工作元件A.B.C独立
则系统正常工作的概率为
![]()
![]() ………………12(分)
………………12(分)
19.解:∵![]() 得
得![]()
又∵![]() 的解集为(-1,2)
的解集为(-1,2)
∴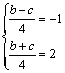 得b=2……………………………………2(分)
得b=2……………………………………2(分)
(Ⅰ)函数![]() 在
在![]() 上为增函数…………4(分)
上为增函数…………4(分)
证明:设![]()
则![]()
∵![]() ∴
∴![]()
∴![]() 即
即![]()
∴函数![]() 在
在![]() 上为增函数………………6(分)
上为增函数………………6(分)
(Ⅱ)由![]() 得
得![]() ……………………8(分)
……………………8(分)
①当![]() ,即
,即![]() 时,
时,![]()
②当![]() ,即
,即![]() 时,无解
时,无解
③当![]() ,即
,即![]() 时,
时,![]()
∴当![]() 时,解集为
时,解集为![]()
当![]() 时,解集为空集
时,解集为空集
当![]() 时,解集为
时,解集为![]() …………………………12(分)
…………………………12(分)
![]() 20.建立如示空间直角坐标系,则
20.建立如示空间直角坐标系,则
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
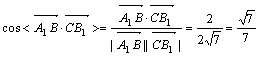
异面直线A1B与CB1所成的角为![]() ………………6(分)
………………6(分)
(Ⅱ)答:存在这样的点Q,使得面QBC与面A1BC成30°角.
解:∵是直三棱柱,又∠ACB=90°,∴BC⊥CA1,BC⊥CC1
∴∠A1CC1是二面角A1-BC-C1所成的平面角
在RtΔA1C1C中,∠A1CC1=60°……………………………8(分)
在A1B1边上取一点Q,在平面A1B1C1中作QP∥B1C1,交A1C1于P,连PC
过证P.Q.B.C共面
∴∠A1CP就是Q—BC—A1的平面角为30°…………………10(分)
∵30°<60°,故有在点P,在角A1CC1的平分线上
在RtΔPC1C中,可得![]()
又A1B1=![]() ,由相似比可得,Q在距点A
,由相似比可得,Q在距点A![]() 处(或距B1点
处(或距B1点![]() 处)……12(分)
处)……12(分)
21.(Ⅰ)解:令![]()
则![]() 即
即![]()
即![]()
又∵![]() ∴
∴![]() ……………………3(分)
……………………3(分)
所求轨迹方程为![]() …………………………………………6(分)
…………………………………………6(分)
(Ⅱ)解:由条件(2)可知OAB不共线,故直线AB的斜率存在
设AB方程为![]()
则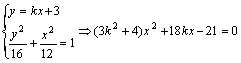 ………………………8(分)
………………………8(分)
![]()
![]()
![]()
∵OAPB为矩形,∴OA⊥OB ![]() ……………………10(分)
……………………10(分)
∴![]() 得
得![]()
所求直线方程为![]() ……………………………12(分)
……………………………12(分)
22.(Ⅰ)解:n=3时,直线x=0上有(0,0)(0,1)(0,2)(0,3)个点,直线x=1上有(1,0)(1,1)(1,2),直线x=2上有(2,0)(2,1),直线x=3上有(3,0)
所以![]() ……………………………4(分)
……………………………4(分)
(Ⅱ)解:n=1时,b1=3, a1=0
n=2时,b1=6, a2=0
当n≥3时,![]()
![]()
当n=1.2时也满足
所以![]() ……………9(分)
……………9(分)
(Ⅲ)对于![]() 个整点中的每一个点都有4种着色方法,故
个整点中的每一个点都有4种着色方法,故![]()
对于![]() 个整点中的每一个点都有2种着色方法,故
个整点中的每一个点都有2种着色方法,故![]() ……11(分)
……11(分)
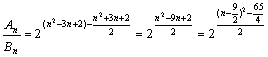
当n=1.2.3.4.5.6.7.8时![]()
当n≥9且n∈N*时,![]() …………………………………14(分)
…………………………………14(分)