高三一模适应性考试数学试卷
姓名 得分
一、选择题(本大题共12小题,每小题5分,共60分)
1. 已知集合![]() ,
,![]() ,则集合
,则集合![]() 的非空真子集的个数为 ( )
的非空真子集的个数为 ( )
A.14 B.15 C.4 D.16
2.条件“![]() ”是条件“
”是条件“![]() ”的 ( )
”的 ( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既非充分又非必要条件
3.已知向量![]() 与
与![]() 同向,则下列等式成立的是 ( )
同向,则下列等式成立的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.设m,n是不重合的两直线,α,β是不重合的两个平面,给出下列命题
(1)若n∥α,α⊥β,则n⊥β (2)若m⊥n,n⊥α,m⊥β,则α⊥β
(3)若n⊥α,α⊥β,m![]() β,则m∥n (4)若n⊥β,α⊥β,则n∥α或n
β,则m∥n (4)若n⊥β,α⊥β,则n∥α或n![]() α
α
其中正确命题的序号是 ( )
A.(1)(4) B.(2)(4) C.(2)(3) D.(3)(4)
5.在等差数列![]() 中,若
中,若![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.14 B.15 C.16 D.17
6.已知函数f(x)=2x的反函数为f-1(x),若f-1(a)+ f-1(b)=4,则![]() 最小值为 ( )
最小值为 ( )
A.1 B.![]() C.
C.![]() D.
D.![]()
7.已知曲线f(x)=xn(n为正偶数,a,x∈R),若![]() ,则以a-a为半径的球的表面积是( )
,则以a-a为半径的球的表面积是( )
A.16π B.8π C.π D.8![]() π
π
8.若函数![]() 的图象和
的图象和![]() 的图象关于点
的图象关于点![]() 对称,则
对称,则![]() 的表达式是( )
的表达式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.过函数![]() 的图象的对称中心,且与抛物线
的图象的对称中心,且与抛物线![]() 有且只有一个公共点的直线的条数共有 ( )
有且只有一个公共点的直线的条数共有 ( )
A.1条 B.2条 C.3条 D.不存在
10.设![]() 是曲线
是曲线![]() 上的点,
上的点,![]() ,
,![]() ,则 ( )
,则 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知函数![]() 具有如下性质:①若
具有如下性质:①若![]() ,则
,则![]() ;②若
;②若![]()
![]() ,则点
,则点![]() 与点
与点![]() 连线的斜率大于
连线的斜率大于![]() ;那么下列具有已知函数性质的是 ( )
;那么下列具有已知函数性质的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.设![]() 为双曲线
为双曲线![]() 右支上异于顶点的任意一点,
右支上异于顶点的任意一点,![]() 、
、![]() 为两个焦点,则
为两个焦点,则![]() 的内心
的内心![]() 的轨迹方程是 ( )
的轨迹方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中横线上)
13.![]() 的展开式中,含
的展开式中,含![]() 项的系数为_________________
项的系数为_________________
14.设集合A={1,2,3,4,5,6},映射![]() 满足
满足![]() ,则这种映射
,则这种映射![]() 的个数为(用数字作答)_________________;
的个数为(用数字作答)_________________;
15.在棱长为1的正方体![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 和
和![]() 的中点,则点
的中点,则点![]() 到
到
平面![]() 的距离为
;
的距离为
;
16.设![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() ,给出下列四个结论:
,给出下列四个结论:
①![]() ; ②
; ②![]() 是以4为周期的函数;
是以4为周期的函数;
③![]() 的图象关于
的图象关于![]() 轴对称; ④
轴对称; ④![]() 。
。
其中正确命题的序号是__ .
三、解答题(本大题共6小题,共74分,解答应有证明过程或演算步骤)
17.已知A(3,0),B(0,3),C(cosα,sinα) (1)若![]() ,求sin2α的值;
,求sin2α的值;
(2)若![]() ,且α∈(0,π),求
,且α∈(0,π),求![]() 与
与![]() 的夹角。
的夹角。
18.平面上有两个质点A、B分别位于![]() ,(
,(![]() ,在某一时刻同时开始每隔一秒钟向上下左右任一方向移动1个单位,已知质点A向左、右移动的概率都是
,在某一时刻同时开始每隔一秒钟向上下左右任一方向移动1个单位,已知质点A向左、右移动的概率都是![]() ,向上、下移动的概率分别是
,向上、下移动的概率分别是![]() 和
和![]() ,质点B向各个方向移动的概率都是
,质点B向各个方向移动的概率都是![]() 。求:(1)点A经过2秒钟到达点
。求:(1)点A经过2秒钟到达点![]() 的概率;(2)A、B经过3秒钟,同时到达点
的概率;(2)A、B经过3秒钟,同时到达点![]() 的概率。
的概率。
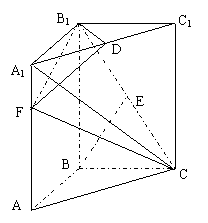
19.如图,直三棱柱![]() 中,底面是以
中,底面是以![]() 为直角的等腰三角形
为直角的等腰三角形![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,
(1)求直线![]() 与
与![]() 所成的角;
所成的角;
(2)在线段![]() 上取一点
上取一点![]() ,使
,使![]() ,求证:
,求证:![]() ⊥平面
⊥平面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 所成的锐二面角的大小。
所成的锐二面角的大小。
20.已知数列![]() ,其中
,其中![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() (1)求数列
(1)求数列![]() 的通项公式; (2)求数列
的通项公式; (2)求数列![]() 的通项公式;(3)数列
的通项公式;(3)数列![]() 的前
的前![]() 项和
项和![]() 。
。
21.设![]() 、
、![]() 分别为三角形
分别为三角形![]() 的重心与外心,
的重心与外心,![]() 、
、![]() ,且
,且![]() ∥
∥![]() 。
。
(1)求点![]() 的轨迹
的轨迹![]() 的方程;(2)已知点
的方程;(2)已知点![]() ,是否存在直线
,是否存在直线![]() ,使
,使![]() 过点
过点![]() 并与曲线
并与曲线![]() 交于
交于![]() 、
、![]() 两点,使
两点,使![]() 为锐角或直角,若存在,求出直线
为锐角或直角,若存在,求出直线![]() 的斜率
的斜率![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
22.已知![]()
(1)若![]() 同时满足下列条件:①
同时满足下列条件:①![]() ;②当
;②当![]() 时,有
时,有![]() ;③
;③![]() 在
在![]() 上的最大值为2。(I)求证:
上的最大值为2。(I)求证:![]() (II)求
(II)求![]() 的解析式;
的解析式;
(2)若![]() ,
,![]() 在[-2,2]上的最大值为
在[-2,2]上的最大值为![]() ,最小值为
,最小值为![]() ,求证:
,求证:![]()
高三一模适应性考试数学试卷评分标准
一、选择题
AADBC BBBBC BA
二、填空题
![]() ;4320;
;4320;![]() ;①②④
;①②④
三、解答题
17、⑴![]()
由![]() 得:
得:
![]()
![]() ……………………4分
……………………4分
平方移项得:![]() ……………………6分
……………………6分
⑵![]()
![]()
![]() ,
,![]() …………………9分
…………………9分
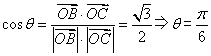 ……………………11分
……………………11分
所以![]() 与
与![]() 的夹角为
的夹角为![]() …………………12分
…………………12分
18、⑴解:![]() 分别表示点
分别表示点![]() 向上、下、左、右移动的概率,点
向上、下、左、右移动的概率,点![]() 要在2秒内到达
要在2秒内到达![]() 点,只能是一秒向上移动,一秒向右移动。所以点
点,只能是一秒向上移动,一秒向右移动。所以点![]() 经过2秒到达
经过2秒到达![]() 点的路线对应“上右”或“右上”两种情况。故所求概率为:
点的路线对应“上右”或“右上”两种情况。故所求概率为:![]() ……6分
……6分
⑵仿⑴可知,经过3秒![]() 点到达
点到达![]() 点的路线对应于“上、上、右”的一个排列,
点的路线对应于“上、上、右”的一个排列,
所以经过3秒后![]() 点到达
点到达![]() 点的概率为:
点的概率为:
![]() ……………………8分
……………………8分
经过3秒![]() 点到达
点到达![]() 点的路线对应于“右、上、下”和“右、左、右”的一个排列
点的路线对应于“右、上、下”和“右、左、右”的一个排列
所以经过3秒后![]() 点到达
点到达![]() 点的概率为:
点的概率为:
![]()
![]() (11分)
(11分)
又因为上述两事件为独立事件,
所以所求概率为:![]() ………………………12分
………………………12分
19、(1)以![]() 点为坐标原点,建立如图的空间直角坐标系,
点为坐标原点,建立如图的空间直角坐标系,
∵![]() ,∴
,∴![]() ,
,
从而![]() ,
,
∴![]() ………………………2分
………………………2分
∴![]() ,
,
∴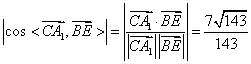 …………………………4分
…………………………4分
∴直线![]() 与
与![]() 所成的角为
所成的角为![]()
(2)由条件知:![]() ∴
∴![]() ,
,
![]() ,
,![]() ,………6分
,………6分
∴![]() ,∴
,∴![]() ⊥平面
⊥平面![]() ………8分
………8分
(3)由上知,平面![]() 的法向量为
的法向量为![]()
平面![]() 的法向量为
的法向量为![]() ,
…………10分
,
…………10分
∴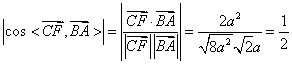 …………11分
…………11分
∴求平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() …………12分
…………12分
20、(1)由条件可得:![]()
累乘得 ![]() ……………………………………4分
……………………………………4分
(2)∵![]() ,∴
,∴![]() ………………………………6分
………………………………6分
而![]() 当
当![]() 时,
时,![]() ,显然
,显然![]() 时也适合;
时也适合;
∴![]() ………………………………8分
………………………………8分
(![]() 不写扣1分)
不写扣1分)
(3)![]() 时,
时,![]() ,即有
,即有![]() 时,
时,![]()
![]() …………………………10分
…………………………10分
![]() 时,
时,![]()
![]()
故 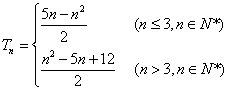 ………………………12分
………………………12分
21、(1)设![]() 则
则![]() ,设外心为
,设外心为![]() ,
,![]()
![]() ∥
∥![]() ,∴
,∴![]() ……2分
……2分
由![]() 得,
得,![]()
化简整理得轨迹![]() 的方程为:
的方程为:![]() ………4分
………4分
(2)设![]() :
:![]() ,
,![]() 、
、![]()
联立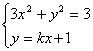 ,消去
,消去![]() 得:
得:![]() ,
,
∴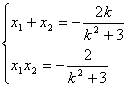 ………6分
………6分
又![]() ,
,![]() ,而
,而![]() 为锐角或直角的充要条件为
为锐角或直角的充要条件为![]() ,即:
,即:![]()
而![]()
![]()
=![]()
∴![]() ,∴
,∴![]() ………11分
………11分
又∵![]() 时,直线
时,直线![]() 过点
过点![]() 不合题意,舍去。
不合题意,舍去。
∴存在直线![]() 使
使![]() 为锐角或直角且直线的斜率
为锐角或直角且直线的斜率![]() 的取值范围是
的取值范围是![]() ――12分
――12分
22、(1)①∵![]() ,
,![]() 且
且![]() 时
时![]() 的最大值是2
的最大值是2
∴![]() ,即
,即![]() ………3分
………3分
②∵![]() 时,
时,![]() ,∴
,∴![]() 即
即![]() (*)
(*)
由(1)知![]() 代入(*)式可得
代入(*)式可得![]() 且
且![]() ,
,
∴![]() ,
,![]() ………6分
………6分
又![]() ,∴
,∴![]() 在
在![]() 处取得最小值,且
处取得最小值,且![]()
∴![]() 的对称轴为
的对称轴为![]() 轴,从而
轴,从而![]() ,
,![]() ,∴
,∴![]() ………8分
………8分
(2)若![]() 则
则![]() 此时
此时![]() ,∴
,∴![]() 在
在![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ,∴
,∴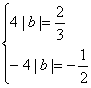 这是不可能的,∴
这是不可能的,∴![]() ………10分
………10分
若![]() ,假设
,假设![]() ,则对称轴
,则对称轴![]() 在
在![]() 外,∴
外,∴![]() 在
在![]() 上是单调函数
上是单调函数
∴![]() ,
,![]() ,同样有
,同样有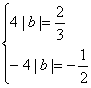 ,这不可能,
,这不可能,
假设不存立,∴![]() ,综上知
,综上知