高中数学习题精选
第二部分·立体几何
三、解答题：
1、直线l为平面α、β的交线，在α、β内各取一点A、B，使它们至l距离相等，求证：AB与α、β所成的角相等。
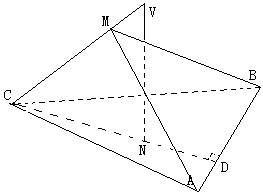
2、VC是△ABC所在平面的斜线，V在平面ABC上的射影N位于△ABC的高CD上，M为VC上一点。若平面AMB与平面ABC所成二面角等于∠CVN。求证：VC⊥平面AMB。
3、二面角M—DC—N 为α度，A为M上一点，
，DC = m，过A作AB交N于B，使AB⊥DC且与半平面N成30°角，求α变化时，
的最大值。
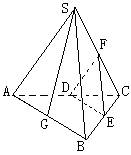
4、SG为正三棱锥S—ABC的斜高，D、E、F分别为AC、BC、SC的中点。
①求证：SG//平面DEF；
②若
，
，求二面角F—DE—C。
5、斜三棱柱
的每条棱长均为a，侧棱与底面成60°角，侧面
垂直于底面。
①求证：
；
②
的体积
。
6、三棱锥S—ABC中，SA = 3，SB = 4，SC = 3，∠BSC = 90°，∠ASB = 60°，顶点S在底面ABC的射影O在△ABC的高CD上，求：
①二面角S—AB—C的大小；
②三棱锥S—ABC的体积
。
7、已知四棱锥P—ABCD的底面为直角梯形，BA⊥AD，CD⊥AD。又AB = 2，CD = 4，侧面PAD⊥ABCD，侧面PBC为一边长为10的正三角形。求侧面PAD与侧面PBC的夹角。
8、圆锥轴截面的顶角∠ASB = 60°，底面直径AB = 2，过S作截面截底面所得
为
底面周长，M为上一动点，MN⊥AO于N。
①M点在何处时，棱锥S—MON的体积最大？
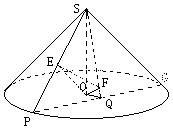②当棱锥S—MON体积最大时，求平面SMN与底面所成二面角的大小。
9、圆锥SO的轴截面为等腰直角三角形，母线长为2a，P、Q分别为底面圆周和底面（非圆周）上的动点，且OQ⊥PQ，E为SP的中点，F为O在SQ上的射影。
①求证：OF⊥平面SPQ；
②求三棱锥S-OEF的体积的最大值。
10、在矩形ABCD中，AD = 2AB，E为AD中点，沿BE将△ABE折起到△A1BE位置，使A1C =
A1D。
①求证：平面A1BE⊥平面BCD；
②求A1C与平面BCD所成的角。
11、在矩形ABCD中，AB = 3，BC = 4，沿对角线BD将△ABD折起，使点A在平面BCD上的射影E恰好落在BC上。
①求AB与CD所成的角的大小；
②求三棱锥A—BCD的体积
。
12、三棱锥S—ABC中∠ASC = ∠SAB = 90°，SA = a，SC = b，AB = c，AB与SC所成的角为α，求证：三棱锥S—ABC的体积
。
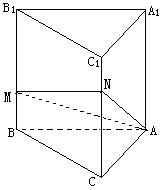
13、正三棱柱
的底面边长为2，高为
，M、N分别为侧棱
、
上的点，且
、
。
①求截面AMN与底面ABC所成二面角的大小；
②求平面AMN与平面ABC所夹柱体部分的体积。
14、四棱锥P—ABCD中，高为5cm，底面为菱形，侧面PAB、PAD都垂直于底面，且这两个侧面成120°的二面角，另两个侧面都与底面成30°的二面角。
①求证：B、C、D都在以A点为圆心的圆周上；
②若此四棱锥P—ABCD表示无底铁皮盖，求沿PC剪开展平再以PA为轴旋转一周所得旋转体的体积。
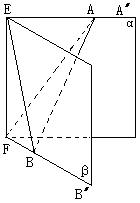
15、
、
在30°的二面角α—EF—β的两个面内，且都与EF垂直，动线段AB的两端点A、B分别在、上移动。当
，
时，求锥体B—AEF的体积的最大值。
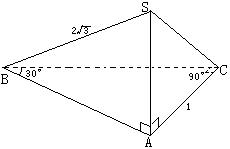16、三棱锥S—ABC中，SA⊥平面ABC，△ABC为Rt△，∠ACB=90°，∠ABC=30°，AC = 1，SB=
。
①求证：SC⊥BC；
②求SC与平面SAB所成角的大小。
17、四棱锥P—ABCD的底面ABCD是平行四边形，
PA⊥底面ABCD，E是PA上的点，PC//截面BDE。
①求P—ABCD被截面BDE分成两部分的体积比；
②若ABCD为矩形，AB∶BC∶PA = 1∶∶1，求二面角E—BD—A的大小。
18、长方形ABCD的长AB是宽体BC的倍，将它折成正三棱柱的侧面，使BC与AD重合，而对角线AC与折线EF、GH分别交于M、N点，求平面AMN与底面AEG所成角的度数。
19、正三棱柱S—ABC的高SO = 3，底面边长为
，过AB作截面ABD交SC于D。设—截面与底面所成二面角为α，问α为多少时，SC⊥截面ABD？
参考答案
1、略 2、略 3、
4、45° 5、
6、
，
7、
8、
，
，
9、
10、
11、90°，
12、
13、30°，1 14、
15、
，
16、
17、1∶3或3∶1，30° 18、 30° 19、