高中数学习题精选
第三部分·解析几何
三、解答题：
1、数轴一两动点P、Q分别从原点与点
出发，t秒后P点坐标为
，Q点坐标为
。
①P、Q两点重合时，求t的值；
②出发2秒后，求线段PQ中点M移动的路程之总和。
2、给定双曲线
，过点
能否作直线m，使得B为m与所给双曲线两交点间线段的中点？这样的直线是否存在？若存在请写出m的方程；若不存在请说明理由。
3、给定
和
两点，在x轴上求一点P，使θ=∠APB取得最大值。
4、过点
的直线
遭到两定直线
、
分别交于P、Q两点。
①设PQ中点为
，试用k表示x、y；
②当k变化时，求PQ中点M的轨迹方程。
5、已知点P在直线x = 2上移动，直线L通过原点且与OP垂直，过点
用P点的直线m与L交于Q点，求点Q的轨迹方程，并给出轨迹名称。
6、△ABC顶点B、C的坐标分别为
、
，AB边上的中线长为m，求点A的轨迹。
7、已知曲线
，它与x正半轴交于A点，与y轴交于B点。
求证：直线AB的倾斜角为定角。
8、已知直线
交抛物线
于A、B两点，P在线段AB上，且OA、OP、OB的倒数成等差数列，求当k变化时，P点的轨迹。
9、已知圆C与
相切，圆心为
，求C的方程。
10、一个圆过双曲线
的两个焦点，且与x轴将于两点，这两点间的距离为8，求此圆的方程。
11、已知
为椭圆
上一动点，点P和定点
之间的距离PQ的最小值为1，试确定a的值。
12、已知直线L的方程为
，曲线C的方程为
，以曲线C的焦点为焦点作椭圆T使椭圆T与L有公共点，求椭圆T的长轴的最小值和此时T的方程。
13、设一列椭圆的左顶点均在
上，它们的长轴长都为4，且都以y轴为左准线，求离心率达到最大值时椭圆的方程。
14、已知椭圆的焦点为
、
，P为椭圆上一点，且
是
与
的等差中项。
①求椭圆的方程；
②若点P在第三象限，且
，求△
的面积。
15、已知直线l交曲线
于M、N两点，点
是椭圆的一个顶点。若△BMN的重心恰好位于椭圆的右焦点F，试求直线l。
16、已知
的离心率
，左、右焦点分别为
、
，左准线为L，能否在双曲线左半支上找一点P，使得是P到L的距离d和的等比中项？若能，请写出P的坐标；若不能请说明理由。
17、曲线
和
交于A、B两点，求以OA、OB为渐近线、实轴长为12的双曲线方程。
18、已知曲线
：
。
①求与有相同渐近线且过点
的双曲线
的方程；
②过的右焦点作倾斜角为45°的直线l，求l被截得的线段长。
19、若△ABC的顶点在抛物线
上，且点A的纵坐标
，△ABC的重心恰好是抛物线的焦点，求直线BC的方程。
20、给定抛物线C：
。若其焦点与准线分别是椭圆E的一个焦点和一条准线，求椭圆E的短轴端点的方程。
21、给定曲线C：
，过点A
的直线l交C于不同的两点P、Q，求以OP、OQ为相邻两边的平行四边形的第四个顶点的轨迹方程，并指明名称、形状、位置。
22、①试确定m、n应满足的条件，使椭圆
与抛物线
有四个交点；
②当m = n = 4 时，证明四个交点共圆。
参考答案
1、①
；②
2、不存在 3、
4、①
，
；②
5、
6、
7、45° 8、
9、
10、
11、a = 2 12、
13、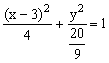
14、
，
15、
16、略
17、
，
18、
19、
20、
21、
（位于
上方及
下方两部分，但不含、两点）
22、①
高中数学习题空荡荡