高中数学习题精选
第三部分·解析几何
二、填空题：
1、直线l过点
，被直线
与
所截线段中点在直线
上，则直线l的方程为＿＿＿＿＿＿。
2、已知点P为直线l上一点，将直线l绕P点沿顺时针方向旋转α角
，所得直线方程为
，若继续旋转
角，所得VC是△ABC所在平面的斜线，V在平面直线为，则直线l的方程为＿＿＿＿＿＿。
3、已知直线
与
关于直线y = x对称，又已知直线的方程为
，直线的方程为
，则
＿＿＿＿＿＿。
4、过坐标原点并与直线
垂直的直线方程为＿＿＿＿＿＿。
5、若直线
与椭圆
交于A、B两点，则
＿＿＿＿＿＿。。
6、如果直线
和
的交点为
，那么过点
和
的直线方程为＿＿＿＿＿＿。
7、若直线方程
中，a、b可从0、1、2、3、4五个数中任取（可重复），则不同的直线有＿＿＿＿＿＿条。
8、若直线l上任一点到直线
和
的距离相等，则直线l的方程为＿＿＿＿＿＿。
9、方程
所表示的圆锥曲线是＿＿＿＿＿＿。
10、过曲线
的右焦点作倾斜角为
的直线，交圆锥曲线于两点，则两点的极坐标分别为＿＿＿＿＿＿和＿＿＿＿＿＿，这两点间的距离为＿＿＿＿＿＿。
11、指出
表示的曲线名称：当
时为＿＿＿＿＿＿；当
时为＿＿＿＿＿＿，当
时为＿＿＿＿＿＿，当
时为＿＿＿＿＿＿。
12、圆锥曲线
的通径长为＿＿＿＿＿＿。
13、设O为坐标原点，则过点
并且垂直于OA的直线方程为＿＿＿＿＿。
14、圆锥曲线
的两条准线之间的距离为＿＿＿＿＿＿。
15、圆锥曲线
的焦距为＿＿＿＿＿＿，
的实轴长为＿＿＿＿＿＿。
16、若方程
的图象为双曲线，则λ的取值范围是＿＿＿＿＿＿。
17、过极点且与极轴夹角为
的直线交抛物线
于A、B两点，则＿＿＿＿。
18、参数方程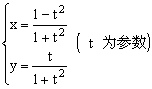
的普通方程为＿＿＿＿＿＿。
19、抛物线
的三条焦半径之长
、
、
成等差数列，且OA、OC对应的极角分别为和
，则B点的极坐标为＿＿＿＿＿＿。
20、双曲线
的实轴长为＿＿＿＿＿＿。
21、直线的参数为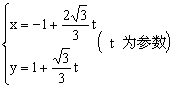
，的极坐标方程为
，则与的夹角α为＿＿＿＿＿＿。
22、椭圆的极坐标方程为
，其准线的极坐标方程为＿＿＿＿＿＿。
23、方程
表示的曲线可能是＿＿＿＿＿＿。
24、过
、
的圆与x轴交于两点所得弦长为8，则此圆的方程为＿＿＿＿＿＿。
25、和圆
外切，且与y轴相切的动圆的圆心的轨迹方程为＿＿＿＿＿＿。
26、点P为圆
上一动点，点A的坐标为
，点Q分线段AP之比为AQ∶QP = 3，则点Q的轨迹方程为＿＿＿＿＿＿。
27、若椭圆两焦点为
、
，过
的弦为AB，且△AB
的周长为20，则此椭圆的方程为＿＿＿＿＿＿。
28、椭圆短轴的一个端点与椭圆的两个焦点恰好为某等边三角形的三个顶点，则此椭圆的离心率e = ＿＿＿＿＿＿。
29、若椭圆
的一条准线方程为
，则m = ＿＿＿＿＿＿。
30、以双曲线
的顶点为焦点的椭圆的准线方程为＿＿＿＿＿＿。
31、已知椭圆中心是
、
所连线的三等分点且x轴、y轴分别是该椭圆的准线和切线，则该椭圆的方程为＿＿＿＿＿＿。
32、若椭圆
上一点P与焦点、的连线互相垂直，则△P的面积为＿＿＿。
33、P为椭圆
上的点（非长轴两端点），、为焦点，A为△P的内心，PA的延长线交于点B，则BA∶AP之值为＿＿＿＿＿＿。
34、双曲线
的渐近线为＿＿＿＿＿＿。
35、已知双曲线的两条渐近线方程分别为
和
，一个顶点的坐标是
，则该双曲线的方程为＿＿＿＿＿＿。
36、若双曲线两准线间的距离的4倍等于焦距，则其离心率e =＿＿＿＿＿＿。
37、已知双曲线的渐近线方程是
，焦点在坐标轴上，中心在原点（原题无，疑为丢失），焦距为10，则该双曲线的方程为＿＿＿＿＿＿。
38、若一双曲线的实轴的长为2a，焦点为、，弦AB过，且
，则AB=＿＿＿＿＿＿。
39、曲线
和
的关系是＿＿＿＿＿＿。
40、设双曲线
的一条渐近线方程为3y = 2x，则过该双曲线上一定点
的切线方程为＿＿＿＿＿＿。
41、双曲线的一条准线方程为x
= 2，其相对应的焦点为
，离心率e =
，则此双曲线的方程为＿＿＿＿＿＿。
参考答案
1、
2、
3、60 4、
5、
6、
7、13 8、
9、椭圆
10、
，
，4 11、直线、双曲线、抛物线、椭圆
12、
13、
14、
15、1，8
16、
17、16 18、
19、
20、4或
21、
22、
，
23、椭圆，双曲线，抛物线 24、
25、
及
26、
27、
28、
29、1 30、
，
31、
32、24 33、
34、
35、
36、2 37、
38、4a
39、相同的焦距 40、
41、