高中数学习题精选
第一部分·代数
三、解答题:
1、在![]() 的图象上有A、B、C三点,此三点横坐标分别为
的图象上有A、B、C三点,此三点横坐标分别为![]() 、
、![]() 、
、![]() 。
。
①若S△ABC=S,求![]() 的表达式。②确定
的表达式。②确定![]() 的单调性。③求
的单调性。③求![]() 的值域。
的值域。
2、解不等式:![]() (若仅知
(若仅知![]() 呢?)
呢?)
3、已知![]() ,
,![]() 为
为![]() 的反函数,又
的反函数,又![]() 。求
。求![]() 的定义域、单调区间和
的定义域、单调区间和![]() 的最小值。
的最小值。
4、方程![]() 的两根中仅有一个较小的根在区间
的两根中仅有一个较小的根在区间![]() 内,试用a表示k的取值范围。
内,试用a表示k的取值范围。
5、![]() ,
,![]() ,a取何实数时
,a取何实数时![]() ?
?
6、在非负整数集N上定义函数![]() ,且有
,且有![]() ,
,![]() ,
,![]() ,其中
,其中![]() 。试用n表示
。试用n表示![]() 的公式,并用数学归纳法证明。
的公式,并用数学归纳法证明。
7、设x满足![]() ,
,![]() 的最大值为0,最小值为
的最大值为0,最小值为![]() 。求实数a。
。求实数a。
8、![]() 是定义在
是定义在![]() 上的函数,且满足
上的函数,且满足![]() 。
。
①求![]() 的定义域;②x为何值时
的定义域;②x为何值时![]() 取得最大值和最小值。
取得最大值和最小值。
9、已知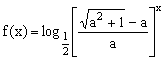 。
。
①判定![]() 的奇偶性;②若
的奇偶性;②若![]() 在
在![]() 为减函数,求a的取值范围。
为减函数,求a的取值范围。
10、已知关于x的方程![]() 的所有解均大于1,求a的取值范围。
的所有解均大于1,求a的取值范围。
11、已知![]() 为单调函数,且
为单调函数,且![]() ,
,![]() ,定义域为R。 ①求证
,定义域为R。 ①求证![]() 为奇函数;②若
为奇函数;②若![]() 满足
满足![]() ,求k的取值范围。
,求k的取值范围。
12、在![]() 的图象上有三点A、B、C,其横坐标分别为
的图象上有三点A、B、C,其横坐标分别为![]() 、
、![]() 、
、![]() 。记△ABC的面积为S。
。记△ABC的面积为S。
①实数m取何值时,S>1;②讨论![]() 时,S的单调性;③
时,S的单调性;③![]() ,求S的取值范围。
,求S的取值范围。
13、已知集合![]() ,定义在集合A上的函数
,定义在集合A上的函数![]() 的最大值和最小值差1,求底数a的范围。
的最大值和最小值差1,求底数a的范围。
14、a为何实数时,对于区间[2,8]上任何实数x,不等式![]() 恒成立?
恒成立?
15、给定函数![]() ,求使y
,求使y![]() 0的x的取值范围。
0的x的取值范围。
16、函数![]() ,x取何值时y
,x取何值时y![]() 0?
0?
17、求![]() 的解集。
的解集。
18、若![]() ,
,![]() 。
。
①比较![]() 与
与![]() 的大小;②解方程
的大小;②解方程![]() 。
。
19、若x![]() 1,求证
1,求证![]() 。
。
20、已知定义在R上的偶函数![]() 满足
满足![]() 。
。
①求证![]() 是以2a为周期的周期函数;
是以2a为周期的周期函数;
②若解![]() 时,
时,![]() 。试求
。试求![]() 在R上的解析式。
在R上的解析式。
③当a = 4时,![]() =0在[0,4]内有且仅有一根2,求
=0在[0,4]内有且仅有一根2,求![]() =0在[0,2000]内所有根之和。
=0在[0,2000]内所有根之和。
21、已知![]() ,求
,求![]() 之值。
之值。
22、已知![]() ,求
,求![]() 之值。
之值。
23、已知函数![]() 。
。
①求![]() 时,x的取值范围;
时,x的取值范围;
②求![]() 和
和![]() (最大值和最小值)。
(最大值和最小值)。
24、求证:![]() 。
。
25、若![]() ,求证
,求证![]() 。
。
26、设![]() ,求证:
,求证:![]() 。
。
27、已知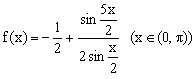 。
。
①将![]() 表示成
表示成![]() 的多项式;
的多项式;
②求![]() 的最小值;
的最小值;
③若![]() 中的
中的![]() 有两个不同的符号,求实数k的取值范围。
有两个不同的符号,求实数k的取值范围。
28、![]() 、
、![]() 、
、![]() 组成公差为
组成公差为![]() 的等差数列,求证:
的等差数列,求证:![]() 。
。
29、△ABC中,三边a、b、c成等差数列,求 ![]() 之值。
之值。
30、已知![]() ,
,![]() ,求
,求![]() 、
、![]() (
(![]() )
)
31、已知△ABC中,![]() ,求证:△ABC为Rt△。
,求证:△ABC为Rt△。
32、已知![]() ,若
,若![]() 在R上的最大值为6,求实数a。
在R上的最大值为6,求实数a。
33、若![]() 且
且![]() ,求证:
,求证:![]() 、
、![]() 、
、![]() 成等差数列。
成等差数列。
34、已知![]() ,
,![]() ,求证:
,求证:![]() 。
。
35、化简:![]() +
+![]() +
+![]() +4
+4![]()
![]()
![]() 。
。
36、设![]() 的两根分别为
的两根分别为![]() 、
、![]() 。求
。求![]() 之值。
之值。
37、A、B、C为△ABC的三内角,a、b、c为其对边,求证:
![]() 。
。
38、当![]() 时,
时,![]() ,求
,求![]() 。
。
39、已知![]() ,
,![]() ,求
,求![]() 。
。
40、若![]() ,化简
,化简![]() 。
。
41、设![]() ,
,![]() ,求
,求![]() 。
。
42、△ABC的三内角为A、B、C,若![]() ,且
,且![]() 、
、![]() 是方程
是方程![]() 的两根,求A和p。
的两根,求A和p。
43、已知:![]() ,
,
求证:![]() 定值。
定值。
44、已知![]() ,且
,且![]() ,求
,求![]() 之值。
之值。
45、已知![]() ,求
,求![]() 之值。
之值。
46、若![]() ,求
,求![]() 的定义域和值域。
的定义域和值域。
47、已知:![]() ,求证:
,求证:![]() 。
。
48、已知:![]() 与
与![]() 是关于x的方程
是关于x的方程![]() 的两根,且
的两根,且![]()
![]() (
(![]() ),
),
求证: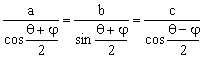 。
。
49、解不等式:![]() 。
。
50、若![]() (
(![]() )恒成立,求实数a。
)恒成立,求实数a。
51、若![]() ,求证:
,求证:![]() 。
。
52、已知:![]() 、
、![]() 、
、![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,
求证:![]() (问何时等号成立?)。
(问何时等号成立?)。
53、a、b、![]() ,求证:
,求证:![]() (问何时等号成立?)。
(问何时等号成立?)。
54、关于实数x的两个不等式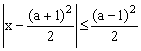 与
与![]() 的解集分别为A和B,求
的解集分别为A和B,求![]() 时实数a的取值范围。
时实数a的取值范围。
55、解关于x的不等式:![]() 。
。
56、解不等式:![]() 。
。
57、解关于x的不等式:![]() 。
。
58、△ABC中,三内角A、B、C成等差数列,且![]() 、
、![]() 、
、![]() 也成等差数列。设内角公差为
也成等差数列。设内角公差为![]()
![]() 。
。
①求证:![]() ;
;
②求和:![]() +
+![]() +
+![]() +
+![]() 。
。
59、数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,
,![]() 时
时![]() 。
。
①若![]() ,求
,求![]() ;
;
②若![]() ,求数列
,求数列![]() 的各项和S;
的各项和S;
③若![]() ,求证:
,求证:![]() 成等差数列。
成等差数列。
60、![]() 中,
中,![]() ,
,![]() 时
时![]()
![]() ,且
,且![]() 。
。
①证明:![]() (
(![]() );
);
②若![]() 且
且![]() ,证明:
,证明:![]() 。
。
61、等比数列![]() 中,首项为复数z,
中,首项为复数z,![]() ,公比
,公比![]() 。以该数列的任意连续三项在复平面上的对应点的顶点的三角形都是直角三角形,且这三项对应的第一个点为直角顶点。求z 。
。以该数列的任意连续三项在复平面上的对应点的顶点的三角形都是直角三角形,且这三项对应的第一个点为直角顶点。求z 。
62、![]() 、
、![]() 、……、
、……、![]() 成等比数列,
成等比数列,![]() =1,
=1,![]() =
= ![]() =1,
=1,![]() ,求Arg
,求Arg![]() 。
。
63、![]() 、
、![]() 在复平面对应的点为P、Q,且
在复平面对应的点为P、Q,且![]() = 4,
= 4,![]() 。
。
求:①S△OPQ; ② ![]() 的最大值。
的最大值。
64、复数![]() ,
,![]() ,
,![]() 。
。
①求证:对任意复数![]() ,△O
,△O![]()
![]() 为直角等腰三角形;
为直角等腰三角形;
②若![]() ,令
,令![]() ,求
,求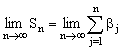 。
。
65、已知![]() ,且
,且![]() ,
,![]() 。
。
①用数学归纳法证明: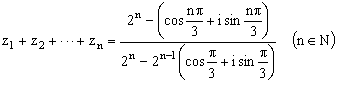
②求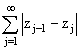 。
。
66、已知复数![]() 在复平面上对应的点
在复平面上对应的点![]() 位于单位圆在第一象限的圆弧上,且
位于单位圆在第一象限的圆弧上,且![]() 。
。
①若![]()
![]() ,求
,求![]() 与
与![]() 的通项;
的通项;
②若![]() ,求
,求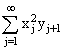 。
。
参考答案
1、①![]() ;②
;②![]() 单调递减;③
单调递减;③![]() 2、
2、![]()
3、[0,1],递增,![]() 时
时![]() 取得最小值
取得最小值![]()
4、![]() ;
;![]() 时
时![]() ,
,![]() 时
时![]() 5、
5、![]()
6、略 7、![]()
8、![]() ,
,![]() 时
时![]() 有最大值
有最大值![]() ,
,![]() 时
时![]() 有最小值
有最小值![]()
9、①奇函数②![]() 10、
10、![]() 11、
11、![]()
12、①![]() ,②单调递减,③
,②单调递减,③![]() 13、
13、![]()
14、![]()
15、![]() 时
时![]() 或
或![]() ;
;![]() 时
时![]() 或
或![]()
16、![]() 时
时![]() ;
;![]() 时
时![]() 17、
17、![]()
18、![]() 或
或![]() 时
时![]() ;
;![]() 时
时![]() ;
;![]() 时
时![]() ;x = 4
;x = 4
19、略 20、①![]() ;
;
②(0,8]内有2,6,[0,2000]内有500个,和为500000。
21、![]() 22、x在二象限时,值为
22、x在二象限时,值为![]() ;x在四象限时,值为
;x在四象限时,值为![]()
23、①![]() ;
;
②![]() 时,
时,![]() ;
;![]() 时,
时,![]()
24、半、倍公式 25、诱导公式 26、差角公式
27、①![]() ;②
;②![]() ;③
;③![]()
28、和角正切 29、![]() 30、
30、![]() ;
;![]()
31、略 32、![]() 33、略 34、略 35、0 36、
33、略 34、略 35、0 36、![]() 37、略
37、略
38、![]() 39、2 40、0 41、7
39、2 40、0 41、7
42、![]() 43、
43、![]() 44、
44、![]() 45、
45、![]() 46、
46、![]()
47、略 48、略 49、![]()
50、![]() 51、略 52、略 53、略 54、
51、略 52、略 53、略 54、![]()
55、![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;
![]() 时,
时,![]() 56、
56、![]()
57、![]() 时,
时,![]() 或
或![]() ;
;![]() 时,
时,![]() 且
且![]() ;
;![]() 时,
时,![]()
58、![]() 59、
59、![]() ;
;![]() ;
;![]() (
(![]() ) 60、略
) 60、略
61、![]() 62、
62、![]() 63、
63、![]()
![]()
64、①略;②![]() ,
,![]() ,
,![]() 65、①略;②
65、①略;②![]()
66、①![]() ,
,![]() ;②
;②![]() ,
,![]()