63、
的最小正周期是＿＿＿＿＿＿。
A. 
B.
π C.
2π D.不存在
64、函数
的定义域是＿＿＿＿＿＿。
A. 
B. 
C. 
D.
65、已知
的图象，要得到
的图象，其变化为＿＿＿＿＿＿。
A. 向左平移 B. 向左平移
C. 向右平移 D. 向右平移
66、若有三个条件：①在区间
内递增；②以π为周期；③是偶函数，则下列四个函数中，同时满足这研修条件的函数是＿＿＿＿＿＿。
A. 
B. 
C.
D.
67、函数
是＿＿＿＿＿＿。
A. 奇函数不是偶函数 B. 偶函数浊奇函数
C. 奇函数也是偶函数 D. 非奇非偶函数
68、
，且
则＿＿＿＿＿＿。
A. 
B. 
C.
D. 
69、下列叙述中正确的是＿＿＿＿＿＿。
A. 是非奇非偶函数 B.
在它的每个周期内都是增函数
C. 
的最小正周期是 D. 
的图象不关于原点对称
70、若
，则
在第＿＿＿＿＿＿象限。
A. 一 B. 二、四 C. 四 D. 二
71、定义在
上的函数
的周期为
。若在区间
上
，则在区间
上的解析式为＿＿＿＿＿＿。
A. 
B.
C.
D.
72、以
为单调增区间的函数是＿＿＿＿＿＿。
A. 
B. 
C. 
D. 
73、
的周期T及最大值M分别是＿＿＿＿＿＿。
A. 
B.
C. 
D.
74、
之值为＿＿＿＿＿＿。
A. 1 B.
45! C.
D.
45
75、
，则
＿＿＿＿＿＿。
A.
B.
C.
D. 或
76、
的最大值为＿＿＿＿＿＿。
A. 
B.
C.
D.
77、已知
，则m的取值范围是＿＿＿＿＿＿。
A.
B. 
C.
D. 
或
78、已知
均为锐角，则下列不等式成立的是＿＿＿＿＿＿。
A. 
B.
C. 
D.
79、设
，则
的充要条件是＿＿＿＿＿＿。
A. 
B. 
C. 
D.以上均不对
80、
成立的一个充分但不必要条件是＿＿＿＿＿＿。
A. 
B. 
C. 
D. 
81、
且
，则△ABC是＿＿＿＿＿＿。
A. 直角三角形或正三角形 B. 正三角形
C. 直角三角形或等腰三角形 D. 等腰不等边三角形
82、若
，则＿＿＿＿＿＿。
A. 
B.
C.
D. 
83、已知
，则
之值为＿＿＿＿＿＿。
A. 1 B. -1 C. 0 D. 不存在
84、如果
，则角
所在象限为＿＿＿＿＿＿。
A. I B. II C. III D.IV
85、与
等值的是＿＿＿＿＿＿。
A. 
B. 
C.
D.
86、关于x的一元二次方程
的两根为
，则
的取值范围是＿＿＿＿＿＿。
A. 
B.
C. 
D. 
87、函数
的最小正周期是＿＿＿＿＿＿。
A. 
B.
C.
D.
88、
是锐角，
,
,
,则有＿＿＿＿＿。
A. 
B.
C.
D.
89、函数
的值域是＿＿＿＿＿＿。
A. 
B.
C.
D.
90、若
，则
=＿＿＿＿＿＿。
A. 
B.
C.
D.
-
91、
是
=a的＿＿＿＿＿＿。
A. 充要条件 B. 充分不必要必要条件
C. 必要非充分条件 D.既不充分也不必要条件
92、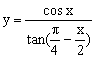
与
的图象关系为＿＿＿＿＿＿。
A. 重合 B. 只有一个公共点 C. 大致一致，局部差异 D.完全不一致
93、
是以5 为周期的奇函数, 
=1，且
，则
=＿＿＿＿＿。
A. 1 B. -1 C. 3 D. 8
94、若A为△ABC一内角，且
，则A=＿＿＿＿＿＿。
A．
B．
C．
D．
95、函数
的值域为＿＿＿＿＿＿。
A. 
B.
C.
D.
96、
的值＿＿＿＿＿＿。
A. 是
B. 是
C. 是
D. 不存在
97、满足
的x的范围是＿＿＿＿＿＿。
A. 
B.
C. 
D.
98、
的值域为＿＿＿＿＿＿。
A.
B.
C. 
D. 
99、
与
是＿＿＿＿＿＿。
A. 增函数 B. 周期函数 C. 奇函数 D. 单调函数
100、下列四个函数中，在定义域内不具有单调性的函数是＿＿＿＿＿＿。
A. 
B. 
C. 
D. 
101、方程
的解集为＿＿＿＿＿＿。
A. 
B.
C. 
D.
以上均错
102、
的值为＿＿＿＿＿＿。
A. 
B.
C.
D.
103、
，
，
，
的大小顺序为＿＿＿＿＿＿。
A. <<<
B. <<<
C. <<<
D. <<<
104、设
，则
的反函数是＿＿＿＿＿＿。
A. 
B. 
C. 
D. 
105、函数
与
的图象间的关系为＿＿＿＿＿＿。
A. 关于x轴对称 B. 关于y轴对称 C. 关于原点对称 D. 关于直线
对称
106、若
，则a、b满足＿＿＿＿＿＿。
A. B.
C.
D. 
107、若
，且
，则
的最小值为＿＿＿＿＿＿。
A. 12 B. 16 C. 6 D. 24
108、数列
的前n项和＿＿＿＿＿＿。
A. 极限为0 B.
极限为1 C.
极限为
D.
极限不存在
109、
是由正数组成的等比数列，且
=81，则
=＿＿＿＿＿＿。
A. 5 B. 10 C. 20 D. 40
110、若
，则
＿＿＿＿＿＿。
A. 2 B. 4 C. 3 D. 2或4
111、若成等比数列，且2
=
，则公比q =＿＿＿＿＿＿。
A. 1或2 B. 1或 -2 C. -1或2 D. -1或 -2
112、若
=
，则
=＿＿＿＿＿＿。
A. 0 B.
1 C.
D.
无法确定
113、用数学归纳法证明
时，从k变到k+1应增添的因式是＿＿＿＿＿＿。
A. 2k+1 B.
C. 
D.
114、在55和555之间插入若干个数，使之与这两数成等差数列，且插入的数中最大者为
展开式中含
项的系数，则插入的数的个数为＿＿＿＿＿＿。
A. 3 B. 4 C. 5 D. 6
115、有一个等差数列，共10项，其中奇数项之和为
，偶数项之和为15，那么该数列第6项为＿＿＿＿＿＿。
A. 3 B. 4 C. 5 D. 6
116、在公比为整数的等比数列中，
，
，则
=＿＿＿＿。
A. 513 B. 512 C.
510 D.
117、已知数列满足
，
，则
＿＿＿＿＿＿。
A. 158 B. 159 C. 160 D. 161
118、在等比数列中，
，
，且
，则
=＿＿＿＿＿＿。
A. 
B.
16 C.
24 D.
32
119、已知数列，若
，则使其前n项和
达到最大值时，n =＿＿＿＿＿。
A. 13 B. 12 C. 11 D. 10
120、在等比数列中，
，
，公比
，则
＿＿＿＿＿。
A. 256 B. -256 C. 512 D. -512
121、设复数
，
，则
的幅角主值为＿＿＿＿＿＿。
A. 
B.
C.
D.
122、复数
的幅角主值为，则k=＿＿＿＿＿。
A. -1 B. -1 或
C.
或 
D.
123、复数
的三角形式为＿＿＿＿＿＿。
A. 
B. 
C. 
D. 
124、复数z满足
，则
、
分别为＿＿＿＿＿＿。
A. 2、1 B. 3、2 C. 3、1 D. 4、2
125、若
是1的6次方根，且
，则
＿＿＿＿。
A. -1 B. 0 C.
1 D.
126、复平面内，按顺时针顺序的A、B、C三点为顶点的三角形为一正三角形，且中心在原点，若A点与复数4对应，则B、C对应的复数分别为＿＿＿＿＿＿。
A. 
、
B.
、
C. 
、 D.
、
127、
,
，则P、Q的关系为＿＿＿＿。
A. 
B.
C.
D.
128、复数
的三角形式为＿＿＿＿＿＿。
A．
B．
C．
D．
129、
、
为不等于0的复数，=
的一个必要但不充分条件是＿＿＿＿＿＿。
A．·=
B．= C．
= D．=
130、若
，则
的最大值是＿＿＿＿＿＿。
A．6 B．
C．
D．不存在
131、复数
是方程
的一个根,则＿＿＿＿＿＿。
A. 
B.
C.
D. 
132、五男二女排一行，若男甲必排在左端或右端，二女必站在一起，则各种可能的不同排法总数等于＿＿＿＿＿＿。
A. 480 B. 360 C. 240 D. 120
133、若
，
，从A、B中各任取一元素作点的坐标，能确定的不同点的个数为＿＿＿＿＿＿。
A. 12 B. 11 C. 23 D. 24
134、若
（n
N）的展开式中含有常数项，则n必为＿＿＿＿＿＿。
A. 奇数 B. 偶数 C. 3的倍数 D. 6的倍数
135、
，则n=＿＿＿＿＿＿。
A. 14 B. 12 C. 13 D. 15
136、从5 名教师和5名学生组成的代表队中选出4人参加一场辩论赛，规定成员中必须有教师和学生，则不同的选法种数是＿＿＿＿＿＿。
A. 150 B. 200 C. 50 D. 25
137、5位同学站一排，其中甲不站中间，则不同的站法有＿＿＿＿＿＿。
A. 24种 B. 96种 C. 116种 D. 119种
138、已知
的展开式中，所有项的系数和等于6561，则展开式中
的系数为＿＿＿＿。
A. 56 B. 448 C. 1120 D. 70
139、用1、2、3、4四个数字组成没有重复数字的四位数，并将它们从小到大排成一列，则四位数2431是这个数列的＿＿＿＿＿＿。
A. 第11项 B. 第12项 C. 第13项 D. 第14项
140、将2封信投入3个信箱，可能的投法种数＿＿＿＿＿＿。
A. 12 B. 8 C. 6 D. 9
141、以 0、1、2、3、4、5组成没有重复数字的6位数，其中偶数的个数是＿＿＿＿＿＿。
A. 
B.
C.
D.
142、七人排成一列，要求甲乙二人之间正好间隔两个人的排法种数共有＿＿＿＿＿＿。
A. 960 B. 480 C. 240 D. 120
143、在
的展开式中，有理项的个数为＿＿＿＿＿＿。
A. 7 B. 8 C. 9 D. 以上均错
144、某单位有4名男同志，3名女同志。现在要组织一个有男有女的小组，规定小组中男同志的数目为偶数，女同志的数目为奇数，则不同的组织方法有＿＿＿＿＿＿。
A．28种 B．324种 C．18种 D．36种
145、某电子元件电路中有一个由三节电阻串联组成的回路，共有6个焊点。若其中某一焊点脱落，电路就不通了。现今回路不通，焊点脱落情况的可能共有＿＿＿＿＿＿种。
A．6 B．63 C．64 D．5
146、从1、2、3、……、21中任取若干个数相加，其和为偶数的取法种数有＿＿＿＿＿＿。
A．
B．
C．
D．
147、四个同学，争夺三项竞赛冠军，冠军获得者的可能有的种数为＿＿＿＿＿＿。
A. 
B.
C.
D.
148、设有4个不同的红球和6个不同的白球，每次从中取四个球，取得红球记2分，取得白球记1分。使得总分不少于5分的所有取法种数为＿＿＿＿＿＿。
A. 
+
+
+
B. 
C. 
D.
149、下列等式中不正确的是＿＿＿＿＿＿。
A. 
B. 
C. 
D. 
150、现有印着0、1、3、5、7、9的六张卡片，如果允许9可以作6使用，则从中抽取3张卡片可以组成不同的三位数的个数是＿＿＿＿＿＿。
A. 152 B. 172 C. 180 D. 210
151、编号为1、2、3、4、5的五个人分别坐在编号为1、2、3、4、5的座位上，则至多两个号码一致的坐法种数为＿＿＿＿＿＿。
A. 109 B. 120 C. 110 D. 119
152、把字母a、a、a、a、b、b、b排成一列，其中任何两个b不能相邻的排法种数有＿＿＿。
A. 
B.
C.
D.
153、有5张卡片的正反面分别写有0与1、2与3、4与5、6与7、8与9。将其中任三张并排组成三位数。可组成不重复的三位数的个数为＿＿＿＿＿＿。
A. 480 B. 432 C. 48 D. 192
参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| D | A | C | D | D | C | B | D | C | C | A | A | B | D |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| A | A | A | A | B | D | D | D | B | D | B | C | C | B |
| 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 |
| D | B | A | B | A | A | C | C | C | D | A | D | A | A |
| 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 |
| A | D | D | C | B | D | B | A | B | D | C | D | B | D |
| 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| D | C | C | C | B | B | B | A | D | D | A | D | C | D |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 |
| A | C | C | C | A | C | A | D | B | A | A | B | D | D |
| 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 |
| D | C | D | A | A | D | B | C | B | D | C | C | B | C |
| 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 |
| C | D | A | A | D | C | B | C | B | C | C | B | C | A |
| 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 |
| B | B | A | C | D | A | B | C | A | B | C | C | D | D |
| 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 |
| D | D | B | B | D | A | C | C | A | B | B | B | B | D |
| 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 | 151 | 152 | 153 | 题号 |
| A | A | C | A | B | A | C | A | B | A | A | A | B | 答案 |