高考第一次模拟测试题数学
本试卷分第I卷(选择题)和第Ⅱ卷两部分。第I卷1至3页,第Ⅱ卷4至10页。共150分。考试时间120分钟。
第Ⅰ卷(选择题 共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡
皮擦干净后,再选涂其它答案,不能答在试题卷上。
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B)
![]() 其中R表示球的半径
其中R表示球的半径
如果事件A、B相互独立,那么 球的体积公式
P(A·B)=P(A)·P(B) ![]() 其中R表示球的半径
其中R表示球的半径
如果事件A在一次试验中发生的概率是P. 那么n次独立重复试验中恰好发生k次的
概率 ![]()
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 函数![]() 存在反函数的充要条件是( )
存在反函数的充要条件是( )
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D) ![]()
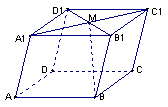
2. 如图:在平行六面体![]() 中,
中,![]() 为
为![]() 与
与![]() 的交点。若
的交点。若![]() ,
,![]() ,
,![]() ,则下列向量中与
,则下列向量中与![]() 相等的向量是( )
相等的向量是( )
 (A)
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
3.设y=8x2-lnx,则此函数在区间 (0,![]() ) 和 (
) 和 (![]() ,1)内分别为( )
,1)内分别为( )
(A) 单调递增,单调递减 (B) 单调递增,单调递增
(C) 单调递减,单调递增 (D) 单调递减,单调递减
4.已知集合![]() ,且
,且![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
(A) ![]() (B)
(B) ![]() (C)
(C)
![]() (D)
(D)
![]()
5.已知椭圆:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 、
、![]() ,以
,以![]() 为顶点,
为顶点,![]() 为焦点的抛物线经过椭圆短轴的两端点,则椭圆的离心率为( )
为焦点的抛物线经过椭圆短轴的两端点,则椭圆的离心率为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.个好朋友一起去一家公司应聘,公司人事主管通知他们面试时间的时候说:“我们公司要从面试的人中招3个人,你们同时被招聘进来的概率是![]() ”。根据他的话可推断去面试的人有( )个.
”。根据他的话可推断去面试的人有( )个.
(A) 70 (B) 21 (C) 42 (D) 35
7. ![]() (
)
(
)
(A) ![]() (B) 0 (C)
(B) 0 (C) ![]() (D)
(D) ![]()
8.若函数![]()
则![]() 的一个可能的值是( )
的一个可能的值是( )
 (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
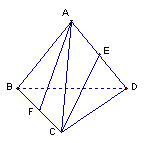
9.如图:在棱长都相等的四面体![]() 中,
中,![]() 、
、![]() 分别
分别
为棱![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() ,则直线
,则直线![]() 、
、![]() 所
所
成角的余弦值为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10.设![]() 、
、![]() 为曲线
为曲线![]() :
: ![]() 的焦点,
的焦点,![]() 是曲线
是曲线![]() :
:![]() 与
与![]() 的一个交点,则
的一个交点,则 的值为( )
的值为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
11.由等式 x4 + a1 x3 + a2 x2 + a3 x + a4= (x+1)4 + b1 (x+1)3 + b2 (x+1)2 + b3 (x+1) + b4, 定义
映射f:(a1,a2,a3,a4)→(b1,b2,b3,b4), 则 f (4,3,2,1) 等于( )
(A)(1,2,3,4) (B)(0,3,4,0) (C)(![]() ,0,2,
,0,2,![]() ) (D)(0,
) (D)(0,![]() ,4,
,4,![]() )
)
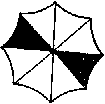 12.某伞厂所生产的伞品种齐全,其中品牌为“太阳伞”的伞的伞蓬都由太阳光的七种颜色组成,这七种颜色分别涂在伞蓬的八个区域内,且恰有一种颜色涂在相对的区域内,则不同颜色图案的此类太阳伞至多有(
)种.
12.某伞厂所生产的伞品种齐全,其中品牌为“太阳伞”的伞的伞蓬都由太阳光的七种颜色组成,这七种颜色分别涂在伞蓬的八个区域内,且恰有一种颜色涂在相对的区域内,则不同颜色图案的此类太阳伞至多有(
)种.
(A) 40320 (B) 5040
(C) 20160 (D) 2520
高考第一次模拟测试题
数 学
第Ⅱ卷(非选择题 共90分)
注意事项:
1.第 Ⅱ 卷共7页,用钢笔或圆珠笔直接答在试题中。
2.答卷前将密封线内的项目填写清楚。
二、填空题(本大题每小题4分,共16分。)
13.在坐标平面内,由不等式组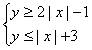 所确定的平面区域的面积为 _________ .
所确定的平面区域的面积为 _________ .
14.过点![]() 的直线
的直线![]() 将圆:
将圆:![]() 分成两段弧,当其中的劣弧最短时,直线
分成两段弧,当其中的劣弧最短时,直线![]() 的方程为 _______ .
的方程为 _______ .
15.球面上有三点![]() 、
、![]() 、
、![]() 组成球的内接三角形,若
组成球的内接三角形,若![]() ,
,![]() ,
,![]() 。且球心到
。且球心到![]() 所在的平面的距离等于球的半径的
所在的平面的距离等于球的半径的![]() ,那么这个球的球面面积为 ______ .
,那么这个球的球面面积为 ______ .
16.正项等比数列{an}满足a2·a4=81, S3=13, bn=log3an则
![]() ____
.
____
.
三、解答题:(本大题共6小题,共74分)
17.(本小题满分12分)
四边形ABCD中,BD是它的一条对角线,且![]() ,
,![]()
求数量积![]() 的值.
的值.
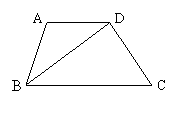 |
18.(本小题满分12分)
已知![]() ,又数列{
,又数列{![]() }(
}(![]() >0) 中,
>0) 中,![]() ,这数列的前n项和
,这数列的前n项和![]() 对所有大于1的自然数n都有
对所有大于1的自然数n都有![]() ,求通项公式
,求通项公式![]() ,并写出推导过程.
,并写出推导过程.
19.(本小题满分12分)
 如图:直三棱柱
如图:直三棱柱![]() 中,
中,![]() ,
,![]() 。
。![]() 为
为![]() 的中点,
的中点,![]() 点在
点在![]() 上且
上且![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
20.(本小题满分12分)
甲,乙两射击运动员进行射击比赛,射击相同的次数,已知两运动员射击的环数![]() 稳定在7,8,9,10环。他们的这次成绩画成频率直方分布图如下:
稳定在7,8,9,10环。他们的这次成绩画成频率直方分布图如下:
击中频率 击中频率
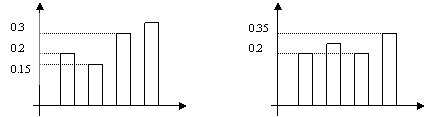
7 8 9 10 击中环数 7 8 9 10 击中环数
甲 乙
(Ⅰ)根据这次比赛的成绩频率直方分布图推断乙击中8环的概率![]() , 以及求甲,乙同时击中9环以上(包括9环)的概率;
, 以及求甲,乙同时击中9环以上(包括9环)的概率;
(Ⅱ)根据这次比赛的成绩估计甲,乙谁的水平更高(即平均每次射击的环数谁大).
21.(本小题满分12分)
在平面直角坐标系中,![]() 为坐标原点,已知两点
为坐标原点,已知两点![]() 、
、![]() ,若点
,若点![]() 满足
满足![]() (
(![]() ),点
),点![]() 的轨迹与抛物线:
的轨迹与抛物线:![]() 交于
交于![]() 、
、![]() 两点.
两点.
(Ⅰ)求证:![]() ⊥
⊥![]() ;
;
(Ⅱ)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得过点
,使得过点![]() 任作抛物线的一条弦,并以该弦为直径的圆都过原点。若存在,请求出
任作抛物线的一条弦,并以该弦为直径的圆都过原点。若存在,请求出![]() 的值及圆心的轨迹方程;若不存在,请说明理由.
的值及圆心的轨迹方程;若不存在,请说明理由.
22.(本小题满分14分)
已知函数![]() 在
在![]() 上的最小值是
上的最小值是![]()
(Ⅰ) 求![]() ;
;
(Ⅱ) 若![]() ,试比较
,试比较 ![]() 与
与![]() 的大小;
的大小;
(Ⅲ) 在点列 ![]() ,
,![]() ,
,![]() ……
……![]() 中, 是否存在三点,使得以这三
中, 是否存在三点,使得以这三
点为顶点的三角形是直角三角形? 若存在, 求出所有这样的三角形的顶点坐标;若不存在,请说明理由
韶关市2004年高考第一次模拟测试题
数学试题参考答案及评分标准
一、 选择题
(1) A (2) A (3) C (4) A (5) C (6) B (7) A (8) A (9) C (10) B (11) D (12) D
二、 填空题
(13) 16 (14) ![]() (15)
(15) ![]() (16)
(16) ![]()
三、 解答题
(17)解:
|
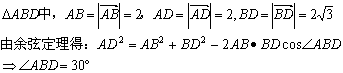 ………………………2分
………………………2分
由
![]() 得
得 ![]() ……………………………………….…4分
……………………………………….…4分
∵
![]() ∴ AD∥BC …………………………………..………….6分
∴ AD∥BC …………………………………..………….6分
∴
![]() 从而
从而 ![]() ………………………..…………8分
………………………..…………8分
∴
![]() . ………………12分
. ………………12分
另解:![]()
![]() .
.
(18)解:∵ ![]() >0 ∴
>0 ∴ ![]()
![]()
![]()
![]() ……..……………………….4分
……..……………………….4分
猜想 ![]() . 下面用数学归纳法证明
. 下面用数学归纳法证明
(1)当![]() 时,由上知结论成立
时,由上知结论成立
(2)假设当![]() 时,结论成立,即
时,结论成立,即![]() ……………………5分
……………………5分
那么,![]()
∴ 当![]() 时,结论也成立. ……………………………………9分
时,结论也成立. ……………………………………9分
由(1)(2),对一切不为零的自然数![]() ,都有
,都有![]() . ……………10分
. ……………10分
则 ![]() ,当
,当![]() 时,
时,![]() ,与题设相符
,与题设相符
故数列{![]() }的通项公式
}的通项公式 ![]() .
……………………………………12分
.
……………………………………12分
(19)解:1)证:依题意知![]() ,
,![]() 且
且
![]() 为
为![]() 的中点,则
的中点,则 ![]() 也为
也为![]() 中点
中点
∴![]() ……………………………………………..3分
……………………………………………..3分
又∵三棱柱![]() 为直三棱柱
为直三棱柱
∴![]()
又 ![]() 且
且 ![]() 、
、![]()
故 ![]() . ……………………………………………6分
. ……………………………………………6分
2)解:由1)知![]() ,在
,在![]() 中过
中过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
连![]() ,由三垂线定理有
,由三垂线定理有![]() 为所求二面角得平面角 ………...8分
为所求二面角得平面角 ………...8分
易知![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]()
故![]()
![]()
在![]() 中
中 ![]()
故所求二面角的大小为![]() . ………………………………………12分
. ………………………………………12分
(20)解(1)由图可知![]() ,
,![]() ,
,![]()
![]() 所以
所以![]() =1—0.2—0.2—0.35=0.25
2分
=1—0.2—0.2—0.35=0.25
2分
同理![]() ,
, ![]() ,
,![]()
所以![]()
![]() 因为
因为![]()
![]() 4分
4分
所以甲,乙同时击中9环以上(包括9环)的概率
![]() P=
P=![]()
![]() =0.65×0.55=0.3575 .
8分
=0.65×0.55=0.3575 .
8分
(2)
因为![]() =7×0.2+8×0.15+9×0.3+10×0.35=8.8
=7×0.2+8×0.15+9×0.3+10×0.35=8.8
![]() =7×0.2+8×0.25+9×0.2+10×0.35=8.7
=7×0.2+8×0.25+9×0.2+10×0.35=8.7
![]()
![]() >
>![]() 所以估计甲的水平更高.
12分
所以估计甲的水平更高.
12分
(21)解:1)解:由![]() (
(![]() )知点
)知点![]() 的轨迹是
的轨迹是![]() 、
、![]() 两点所在的直线,故 点
两点所在的直线,故 点![]() 的轨迹方程是:
的轨迹方程是:![]() 即
即![]() ………… ….2分
………… ….2分
由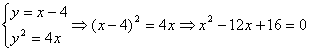
∴![]()
![]()
∴![]()
∴![]() 故
故 ![]() ⊥
⊥![]() . ……………………………………6分
. ……………………………………6分
2)解:存在点![]() ,使得过点
,使得过点![]() 任作抛物线的一条弦,以该弦为直径的圆都过原点
任作抛物线的一条弦,以该弦为直径的圆都过原点
由题意知:弦所在的直线的斜率不为零 …………………………………7分
故 设弦所在的直线方程为:![]() 代入
代入 ![]() 得
得 ![]()
∴ ![]()
![]()
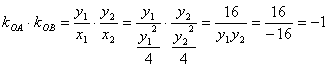
∴![]() 故以
故以![]() 为直径的圆都过原点 …………………………..10分
为直径的圆都过原点 …………………………..10分
设弦![]() 的中点为
的中点为![]() 则
则![]()
![]()
![]()
∴弦![]() 的中点
的中点![]() 的轨迹方程为:
的轨迹方程为:
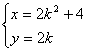 消去
消去![]() 得
得 ![]() . ……………………12分
. ……………………12分
(22)解(1)由![]()
令![]() , ………………………………………….3分
, ………………………………………….3分
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上递减;
上递减;
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上递增;
上递增;
![]()
![]() 在
在![]() 上,当
上,当![]() 时,取得最小值
时,取得最小值![]()
即: ![]()
![]() . ………………………………………………6分
. ………………………………………………6分
(2)由![]()
又![]()
故:![]()
而函数![]() 在
在![]() 上是减函数,故:
上是减函数,故: ![]() <
<![]() . ……………………10分
. ……………………10分
(3)假设存在三点![]() ,
,![]() ,
,![]() ,使⊿ABC是直角三角形.
,使⊿ABC是直角三角形.
不妨设:![]() ,则
,则![]()
+![]() -
-![]()
=![]()
![]()
=![]()
故不存在三点,使以这三点为顶点的三角形为直角三角形. ………………14分