高考适应性考试数学试卷
姓名
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合![]() ,
,![]() ,则
,则![]() 、
、![]() 的关系为 ( )
的关系为 ( )
A.![]() B.
B.![]()
![]() C.
C.![]()
![]() D.
D.![]()
2.一个容量为20的样本,数据的分组及各组的频数如下表:
| 分/组 |
|
|
|
|
|
|
| 频数 | 2 |
| 3 |
| 2 | 4 |
则样本在区间![]() 上的频率为(其中
上的频率为(其中![]() ) ( )
) ( )
A.0.5 B. 0.7 C. 0.25 D. 0.05
3.从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是 ( )
A.至少有1个白球,都是白球 B.至少有1个白球,至少有1个红球
C.恰有1个白球,恰有2个白球 D.至少有1个白球,都是红球
4.由约束条件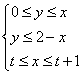 所确定的区域面积为
所确定的区域面积为![]() ,记
,记![]()
![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知双曲线![]() 和椭圆
和椭圆![]() 的离心率互为倒数,那么以
的离心率互为倒数,那么以![]() 为边的三角形一定是 ( )
为边的三角形一定是 ( )
A.等腰三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
6.设一个正多面体的面数为F,顶点数为V,若F+V=8,且它的各条棱长都等于4,则这多面体的外接球的球面面积是 ( )
A.12![]() B.24
B.24![]() C.16
C.16![]() D.28
D.28![]()
7.下列判断中错误的个数是 ( )
(1)命题“若![]() 则
则![]() ”与命题“若
”与命题“若![]() 则
则![]() ”互为逆否命题;
”互为逆否命题;
(2)“![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
(3)在![]() 中,若
中,若![]() ,则
,则![]() ;
;
(4)命题“![]() ”为真命题
”为真命题
A.1个 B.2个 C.3个 D.4个
8.如图,矩形ABCD中,AB=3,BC=4,沿对角线BD将△ABD折起,使A点在平面
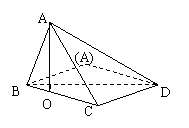 BCD内的射影落在BC边上,若二面角C—AB—D的平面
BCD内的射影落在BC边上,若二面角C—AB—D的平面
角大小为θ,则![]() 的值等于 ( )
的值等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知![]() ,函数
,函数![]() 的图象按向量
的图象按向量![]() 平移得到的图象,恰与直线
平移得到的图象,恰与直线![]() 相切于点
相切于点![]() ,则
,则![]() 的解析式为 ( )
的解析式为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10. 函数![]() 的图象如图所示,则
的图象如图所示,则![]() 的值一定 ( )
的值一定 ( )
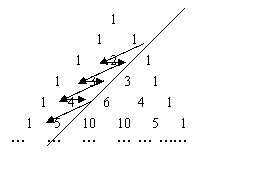 A. 等于0 B.大于0 C.小于0 D.小于或等于
A. 等于0 B.大于0 C.小于0 D.小于或等于![]()
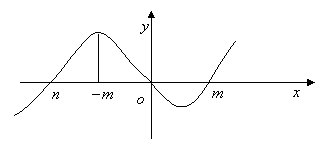
11、如图,在杨辉三角中,斜线![]() 的上方,从1开始箭头所示的数组成一个锯齿形数列:1,3,3,4,6,5,10,……,记其前
的上方,从1开始箭头所示的数组成一个锯齿形数列:1,3,3,4,6,5,10,……,记其前![]() 项和为
项和为![]() ,则
,则![]() 等于 ( )
等于 ( )
A.129 B.172 C.228 D.283
12.2003年12月,全世界爆发"禽流感",科学家经过深入的研究,终于发现了一种细菌M在杀死"禽流感"病毒N的同时能够自身复制.已知1个细菌MD在杀死1个病毒N后,变成了2个细菌M,那么1个细菌M和2047个"禽流感"病毒N最多可生成细菌M的数值是( )
A.1024 B.2047 C.2048 D.2049
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中横线上)
13.过点![]() 和曲线
和曲线![]() (
(![]() )相切的直线与
)相切的直线与![]() 平行,则此直线方程为
平行,则此直线方程为
14.已知数列![]() 的通项公式为
的通项公式为![]() ,则在
,则在![]() 的展开式中,含
的展开式中,含![]() 的项的系数是数列
的项的系数是数列![]() 中的第 项。
中的第 项。
15.已知![]() ,则
,则![]() 的最小值为 。
的最小值为 。
16.点P是双曲线![]() 和圆
和圆![]() 的一个交点,且
的一个交点,且![]() ,其中
,其中![]() 是双曲线
是双曲线![]() 的两个焦点,则双曲线
的两个焦点,则双曲线![]() 的离心率为 。
的离心率为 。
三、解答题(本大题共6小题,共74分,解答题应写出文字说明,证明过程或演算步骤)
17.(12分)已知锐角△ABC中,三个内角为A、B、C,两向量![]() ,
,![]() 是共线向量。
是共线向量。
(I)求∠A的大小;(II)求函数y=2sin2B+cos(![]() )取最大值时,∠B的大小
)取最大值时,∠B的大小
18.(12分)现有10条活鱼养在一水池中,其中有6条鲫鱼,4条鲤鱼,某人每天随机从水池中取出3条鱼进行观察,
(1)若此人将3条鱼一次取出,求取出的3条鱼中两种鱼均出现的概率;
(2)若此人将3条鱼分三次取出,每次取出一条鱼观察后又放回水池中,求第二次、第三次均取到鲤鱼的概率。
19.(12分)如图,已知斜三棱柱ABC—A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=![]() ,且AA1⊥A1C,AA1=A1C.
,且AA1⊥A1C,AA1=A1C.
(1)求侧面A1ABB1与底面ABC所成二面角的大小;
(2)求顶点C到侧面A1ABB1的距离;
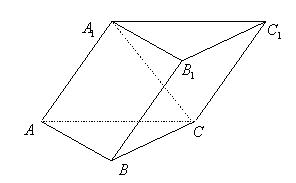 (3)求异面直线
(3)求异面直线![]() 与
与![]() 所成的角。
所成的角。
20.(12分)已知函数![]() 的图象过点
的图象过点![]() ,且在
,且在![]() 处的切线方程为
处的切线方程为![]()
(1)求![]() 的解析式;(2)若
的解析式;(2)若![]() 在
在![]() 上有最小值
上有最小值![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
21.(12分)已知抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,过
,过![]() 上一点
上一点![]() 作抛物线的两条切线,切点分别为
作抛物线的两条切线,切点分别为![]() ,现某学习小组在研究讨论中提出如下三个猜想:
,现某学习小组在研究讨论中提出如下三个猜想:
(1)直线![]() 恒成立;
恒成立;
(2)直线![]() 恒过定点
恒过定点![]() ;
;
(3)等式![]() 中的
中的![]() 恒为常数。请你一一进行验证。
恒为常数。请你一一进行验证。
22.(14分)设![]() 、
、![]() 为两个数列,记
为两个数列,记![]() (
(![]() )
)
(1)求证:![]()
(2)设数列![]() 满足
满足![]() ,
,![]() ,①求证:
,①求证:![]() ,(
,(![]() );
);
②![]()
高考适应性考试
数学试卷评分标准
一、 选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | C | A | D | B | B | A | C | B | D | C |
二、 填空题
| 题号 | 13 | 14 | 15 | 16 |
| 答案 |
| 11 | 16 |
|
三、 解答题
17、解:(1)![]() =(2-2sinA,cosA+sinA),
=(2-2sinA,cosA+sinA),![]() =(sinA-cosA,1+sinA),
=(sinA-cosA,1+sinA),
∵![]() //
//![]() ∴(2-2sinA)(1+sinA)-(cosA+sinA)(sinA-cosA)=0;―――――2分
∴(2-2sinA)(1+sinA)-(cosA+sinA)(sinA-cosA)=0;―――――2分
化简得:![]() ―――――――――――――――――――――――――3分
―――――――――――――――――――――――――3分
∵△ABC为锐角三角形,sinA=![]() ∴A=60° ――――――――――――――6分
∴A=60° ――――――――――――――6分
(2)y=2sin2B+cos(![]() )=2sin2B+cos(
)=2sin2B+cos(![]() )=2sin2B+cos(2B-60°)
)=2sin2B+cos(2B-60°)
=1-cos2B+cos(2B-60°) =1+sin(2B-30°)―――――――――――――――10分
当B=60°时取最大值2―――――――――――――――――――――――――12分
18、解:(1)记“一次取出3条鱼,其中两种鱼均出现”为事件A,――――――――2分
则![]() ――――――――――――――――――――――6分
――――――――――――――――――――――6分
(2)记“每次取出鱼后放回,在三次取鱼中,第二次、第三次均取到鲤鱼”为事件B,“每次取出鱼后放回,第一次取到鲫鱼,第二次、第三次均取到鲤鱼”为事件B1,“每次取出鱼后放回,三次均取到鲤鱼”为事件B2,则![]() ,
,![]() -10分
-10分
∴![]() ―――――――――――――――――――12分
―――――――――――――――――――12分
19、(1)取AC中点D连A1D,则易知A1D![]() 底面
底面![]() ,取AB中点E,连
,取AB中点E,连![]() ,可得DE//BC且DE
,可得DE//BC且DE![]() BC,∴DE⊥AB,由三垂线定理可得A1E⊥AB,∴∠A1ED为侧面A1ABB1与底面ABC的所成二面角的平面角
BC,∴DE⊥AB,由三垂线定理可得A1E⊥AB,∴∠A1ED为侧面A1ABB1与底面ABC的所成二面角的平面角
∵A1D=![]() DE=1 ∴∠A1ED=60°,面A1ABB1与底面ABC的所成二面角为60°―4分
DE=1 ∴∠A1ED=60°,面A1ABB1与底面ABC的所成二面角为60°―4分
(2)设C到侧面A1ABB1的距离为h,∵![]()
又∵![]()
即顶点C到侧面A1ABB1的距离为![]() .-8分
.-8分
(3)取![]() 点为坐标原点,过
点为坐标原点,过![]() 点垂直于
点垂直于![]() 的直线为
的直线为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系。易得:
轴建立空间直角坐标系。易得:![]() 、
、![]() 、
、![]() 、
、![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]()
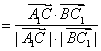
![]()
∴异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ――――――――――――――12分
――――――――――――――12分
20、解:∵![]() ,∴
,∴![]()
又![]() , ∴
, ∴![]() ,
,![]() ,∴
,∴![]()
∴![]() ―――――――――――――――――――――――――4分
―――――――――――――――――――――――――4分
(2)∵![]() ,∴当
,∴当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单调减,在
上单调减,在![]() 上单调增。――――――――6分
上单调增。――――――――6分
又∵![]() ,所以
,所以
①当![]() 时,
时,![]() 在
在![]() 上单调减,故
上单调减,故![]()
![]() ,故
,故![]() 不合题意―――――――――――――――――――――――――――9分
不合题意―――――――――――――――――――――――――――9分
②当![]() 时,
时,![]() ,适合题意。
,适合题意。
综上可得,实数![]() 的取值范围为:
的取值范围为:![]() ―――――――――――――――――12分
―――――――――――――――――12分
21、(1)由![]() ,对其求导得:
,对其求导得:![]() ,
,
设![]() ,则直线
,则直线![]() 的斜率分别为
的斜率分别为![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
同理:直线![]() 的方程为
的方程为![]() ,
,
∴可解得点![]() 的坐标为
的坐标为![]() ,
,
又点![]() 在准线
在准线![]() 上,∴
上,∴![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,猜想(1)成立。――――――――――4分
,猜想(1)成立。――――――――――4分
(另解:设![]() ,则点
,则点![]() 在直线
在直线![]() 上,∴
上,∴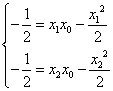 ,∴
,∴![]() 是方程
是方程![]() 的两根,故
的两根,故![]() ,∴
,∴![]() ,∴
,∴![]() ,猜想(1)成立)
,猜想(1)成立)
(2)直线![]() 的斜率
的斜率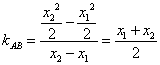 ,
,
∴直线![]() 的方程为
的方程为![]() ,又
,又![]() ,∴
,∴![]() ,
,
显然直线![]() 过焦点
过焦点![]() ,猜想(2)成立。―――――――――――――8分
,猜想(2)成立。―――――――――――――8分
(3)![]() ,
,![]() ,
,
∴![]()
![]()
![]() ,
,
又![]() ,
,
∴![]() ,
,
所以![]() 恒成立,
恒成立,![]() 为常数
为常数![]() 。―――――――――――――――12分
。―――――――――――――――12分
22、(Ⅰ)证明:![]()
=![]() ┈┈┈┈2分
┈┈┈┈2分
=![]()
=![]() ┈┈┈┈┈┈┈┈┈┈┈┈┈5分
┈┈┈┈┈┈┈┈┈┈┈┈┈5分
(Ⅱ)(1)在![]() 个数
个数![]() 中,设正数之和为A,负数之和为B,则A+B=0,A-B=1,∴
中,设正数之和为A,负数之和为B,则A+B=0,A-B=1,∴![]() ,
,![]() ,┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈7分
,┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈7分
所以,![]() ,即
,即![]() ┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈9分
┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈9分
(2)由题意,![]() ,又由题(Ⅰ)知:
,又由题(Ⅰ)知:![]() ┈┈11分
┈┈11分
![]() ,∴
,∴![]() ┈┈┈┈┈┈┈14分
┈┈┈┈┈┈┈14分
(2)证法2 设![]() 中,正数集为M,负数集为N,则
中,正数集为M,负数集为N,则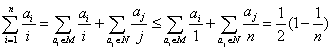 ┈┈┈┈┈┈┈11分
┈┈┈┈┈┈┈11分
又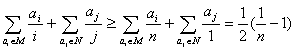 ┈┈┈┈┈┈┈13分
┈┈┈┈┈┈┈13分
∴![]() ,即
,即![]() ┈┈┈┈┈┈┈14分
┈┈┈┈┈┈┈14分