高考数学考前查漏补缺
一. 本周教学内容:
考前查漏补缺
二. 重点知识回顾
从近几年高考试题的革新看,有以下几个特点:(1)题量适当减少,尤其是选择题的个数在减少,今年北京卷的高考试题中调整为8个,但填空题由原来的4个增加至6个;(2)试卷结构更趋合理,通过改革题量及题型,既能更好地考查学生的知识水平,解题能力,又能给学生更多的思维时间和空间,更好地展现学生的思维水平;(3)试题的命制更具综合性与灵活性、新颖性,由于题量的减少,而又要考查的全面,就必然加强知识方法运用的综合性,这符合考试大纲中的“在知识网络的交汇处”命题的原则。此外,近几年的试题中加强了数学的应用意识(每年都会设置一道大的应用题),也在不断探索编制一些情境新颖,或能体现中等数学与高等数学的衔接的一些问题。
从试题的以上特点,不难得出我们的复习策略:
(1)不必猜题、押题,这样做无疑既耗费精力又容易造成复习的不全面;
(2)重视基础知识与方法的全面复习,争取以点带面;
(3)树立整张试卷一盘棋的思想意识,要获取最后的胜利,就需要全局考虑,争取“能得分处多得分,难得分处要争分”;
(4)考前的近半个月可做“温故”工作,即把一模,二模的试题重新检阅,以试题带动重点知识与方法的复习。
近些年的高考试题,对知识的考查既全面又突出重点,对课本中的重点知识与解题方法保持了较高的比例与深度,此外,在考查思维能力的同时,也兼顾考查学生的其他能力,如审题、分析能力,合理表述的能力,等等。常见的问题有:①审题不慎;②计算不准;③表述不当;④时间安排不合理。这些问题往往是导致失分的主要原因,不可不引起大家的重视。
高考试卷中重点考查的知识有哪些呢?不妨做一简略回顾。
(一)函数:定义域、值域、解析式、判断或证明函数的单调性、奇偶性、反函数、最值、图象。
(二)不等式:解不等式、证明不等式(常用比较法、数学归纳法)
(三)数列:两种基本数列(等差数列与等比数列),递推关系式、极限、数学归纳法证明、求和。
(四)三角:正、余弦定理,三角恒等变形、(公式熟、准)、三角函数图象性质、解三角形。
(五)复数:基本的运算、加减法的几何意义。
(六)立体几何:有关直线、平面的位置关系的定理(要熟练),证明直线与平面的平行与垂直,计算空间的角(异面直线成角、线面角、二面角)与距离(点线、点面、线面、面面距离),以及计算多面体或旋转体的表面积、体积。
(七)解析几何:直线方程(包括斜率、倾斜角),点到直线的距离,圆锥曲线的方程、性质,直线与圆锥曲线的位置关系,参数方程与极坐标方程(掌握互化公式是解此类题的通法)
(八)排列组合:两个原理(加法原理、乘法原理)的应用。
【典型例题】
例1. ![]()
分析与解:
显然,这是解对数不等式,方法是化为同底型对数不等式,需要注意的是勿忘“真数>0”。解题时,建议运用等价转化的格式,以使得解题步骤清晰、明朗、简捷;此外,由于要运用对数函数单调性转化不等式,故还需对底数a分类讨论,但不宜太早地分类。
解:![]()
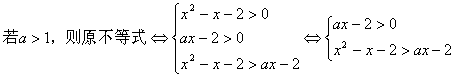
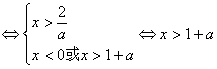
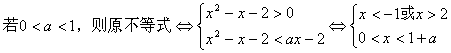
![]()
![]()
![]()
注:解不等式需熟练掌握,它是研究其他问题的重要工具,如求函数定义域、值域,求参数的取值范围等等,也是高考的重点考查内容。
例2. △ABC中,角A、B、C的对边分别为a,b,c,且满足
![]()
(I)求角B的度数;
![]()
分析与解:
(I)已知等式中含有角A、B、C,所求者为角B,故需把角A、C用B表示出来,转化为只含角B的三角方程,由此可求得角B。
(II)已知a+c=3,欲求a,c,只需再建立一个以a、c为未知数的方程,然后与a+c=3联立,既可求a,b的值,注意到由(I)可知角B大小,由余弦定理,可得到a,c的方程。
解:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
注:对三角恒等变形能力的考查通常与解三角形相综合,一方面体现了三角恒等变形的工具性,另一方面,也体现了知识的综合性,需熟练掌握,此外,对三角形恒等变形能力的考查,往往也结合三角函数的性质。例如:
![]()
其最小正周期为π。
(I)求实数a,ω的值;
![]()
答案:(I)a=1,ω=1;
![]()
例3. ![]()
(I)求{an}的通项公式;
![]()
![]()
分析与解:
这是一道有关数列的基本题,已知条件明确指明{an}是等差数列,欲求其通项公式,只需由a2=1及S11=33,解出首项a1及公差d即可;而欲证{bn}是等比数列,只需根据等比
![]()
解:(I)设{an}公差为d,首项为a1,则
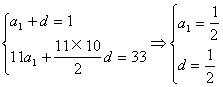
![]()
(II)对任意自然数n,
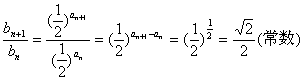
![]()
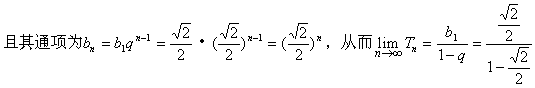
![]()
注:本题不难,但却考查了有关数列的若干重要概念、公式,在考前的复习中,应再多做些此类习题,提高解题的速度与准确。此外,对数列的考查还经常以递推公式为背景考查归纳、探索能力,也常常把数列与函数知识综合考查。
例如:
![]()
![]()
![]()
{an}是否为等差数列?请对你的结论给予证明。
答案:![]()
![]()
例4. ![]()
![]()
(I)求复数Z;
(II)指出点B的轨迹;
![]()
分析与解:
![]()
![]()
解:![]()
![]()
![]()
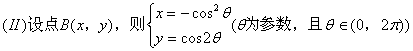
![]()
![]()
![]()
![]()
![]()
注:复数的运算是高考考查的重点,其几何意义则是另一重点,需正确理解,复数与复平面内点之间的对应关系,复数与向量的对应关系,以及向量的加减运算法则——平行四边形法则及三角形法则。
例5. 如图,棱长为1的正方形ABCD—A1B1C1D1中,E是CC1的中点,
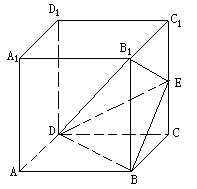
(I)求证:平面B1DE⊥平面B1BD;
(II)求二面角B—B1E—D的余弦值;
(III)求点B1到平面BDE的距离。
分析:(I)欲证平面B1DE⊥平面B1BD,就需根据面面垂直的判定定理,先证线面垂直,尝试发现,图中已有直线皆不合要求,需添加此直线,注意到EB1=ED(等腰三角形),取B1D中点M,则EM⊥B1D,再继证EM⊥BD即可。
(II)由(I)之证明及三垂线定理,可构造二面角的平面角。
(III)点B1到平面BDE的距离可看作三棱锥B1—BDE的面BDE上的高,只需利用“等体积法”求该距离。
(I)证明:取B1D的中点M,连结EM
∵△EB1D中,EB1=ED,∴△EB1D为等腰三角形
∴EM⊥B1D,注意到点M也是AC1的中点,
△C1AC中,E、M分别为两边C1C,C1A的中点,
∴EM∥AC,又AC⊥BD
∴EM⊥BD,
![]()
![]()
∴平面B1DE⊥平面B1BD。
(II)由(I)的结论,若过B作BN⊥DB1于N,则得BN⊥平面B1ED,
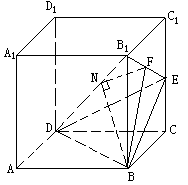
过N作NF⊥B1E于F,连结BF,由三垂线定理,BF⊥B1E,
∴∠BFN是二面角B—B1E—D的平面角,
![]()
(III)设B1到平面BDE的距离为d,
![]()
![]()
![]()
![]()
![]()
例6. ![]()
![]()
(I)求双曲线方程;
![]()
点坐标为(0,-1)且AC=AD,求k的取值范围。
分析:(I)要确定双曲线方程,需待定方程中的a2,b2,只需由已知条件列出关于a2,b2的两个方程即可。
![]()
弦,若CD中点为P,则易得AP⊥CD,从而可联想到kAP·kCD=-1以及中点坐标公式……
解:(I)设双曲线右焦点为(c,0),(c>0),
![]()
![]()
![]()
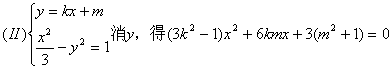
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
【模拟试题】
一、选择:
1. 平面直角坐标系中,两点A(cos80°,sin80°),B(cos20°,sin20°),则AB=( )
A. ![]() B.
B.
![]() C.
C. ![]() D. 1
D. 1
2. 设集合![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 极坐标方程![]() 表示的曲线是( )
表示的曲线是( )
A. 圆 B. 椭圆 C. 抛物线 D. 双曲线
4. 若![]() 的值为( )
的值为( )
A. 3
B. -3 C. -2 D. ![]()
5. 下面四个函数中,以π为最小正周期,且在区间(![]() )上为减函数的是( )
)上为减函数的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 若![]() 的最大值为( )
的最大值为( )
A. 6 B. 5 C. 4 D. 3
7. 设![]() 是两个平面,m、n是两条直线,则下列命题中正确的有( )个。
是两个平面,m、n是两条直线,则下列命题中正确的有( )个。
命题1:若m∥n,m⊥α,则n⊥α; 命题2:若m∥n,m∥α,则n∥α;
命题3:若m⊥α,n⊥β,m∥n,则α∥β; 命题4:若m⊥n,则m⊥α,n⊥β,则α⊥β。
A. 0 B. 1 C. 2 D. 3
8. 已知f(x)是定义在(-3,3)上的奇函数,当![]() 时,f(x)的图象如下图所示,则不等式
时,f(x)的图象如下图所示,则不等式![]() 的解集为( )
的解集为( )
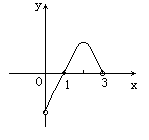
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
二、填空题:
9. P是以F1、F2为焦点的双曲线![]() 上的一点,PF1⊥PF2,且
上的一点,PF1⊥PF2,且![]() 则双曲线的离心率e=___________。
则双曲线的离心率e=___________。
10. 正三棱锥的底面边长为4,体积为1,则侧面与底面所成二面角的大小为___________(可用反三角函数表示)
11. 等差数列{an}中,a1=2,公差不为零,且![]() 恰是某等比数列的前三项,则该等比数列的公比q的值为___________。
恰是某等比数列的前三项,则该等比数列的公比q的值为___________。
12. 把长为12cm的铁丝截成两段,各自围成一个正三角形,则这两个正三角形的面积之和的最小值为___________,此时这两段铁丝长度分别为___________。
13. 函数![]() 的最大值为___________,其单调增区间是___________。
的最大值为___________,其单调增区间是___________。
14. 集合![]() A是S的一个子集,当
A是S的一个子集,当![]() 时,若有
时,若有![]() ,则称x为A的一个“孤立元素”,则S中无“孤立元素”的4元子集的个数是___________个。
,则称x为A的一个“孤立元素”,则S中无“孤立元素”的4元子集的个数是___________个。
三、解答题:
15. 若![]() ,解关于x的不等式
,解关于x的不等式![]() 。
。
16. 已知A是△ABC的一个内角,且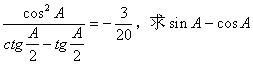 的值。
的值。
17. 数列{an}中,a1=1,前n项和为Sn,对任意![]() ,
,![]() 是等差数列。
是等差数列。
(1)求![]() ;
;
(2)求{an}的通项公式;
(3)求![]() 的值。
的值。
18. 已知a>0,函数![]() 上为单调函数。
上为单调函数。
(1)求实数a的取值范围;
(2)![]() ,求证:
,求证:![]() 。
。
【试题答案】
一、选择:
1. D 2. B 3. D 4. A 5. B 6. C 7. D 8. C
二、填空:
9. ![]() 10.
10. ![]() 11.
11. ![]() 12.
12. ![]()
13. 最大值为![]() ,增区间为
,增区间为![]() 14. 6个
14. 6个
三、解答题:
15. 解:设![]() ,则原不等式可化为
,则原不等式可化为![]()
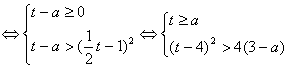
![]()
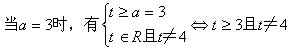
![]()
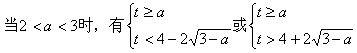
显然,![]()
又∵![]()
∴![]()
∴![]()
∴![]()
综上,可得
当a>3时,原不等式的解集为![]() ;
;
当a=3时,原不等式解集为![]() ;
;
当![]()
![]()
16. 解:∵![]()
∴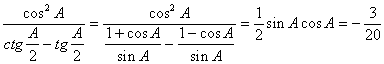
∴![]()
又∵![]()
∴![]()
又∵![]()
∴![]() 。
。
17. 解:由已知,得![]() ,
,
即![]()
(1)计算,可得![]() ,
,
(2)猜测{an}的通项为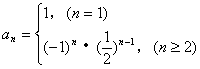
数学归纳法证明(略)
(3)![]()
∴![]()
![]() 。
。
18. 解:(I)任取![]() ,设
,设![]()
![]()
∵![]()
由于不存在常数a,使![]() 恒为负数,而f(x)有明确的单调性,故必有一个常数a,使
恒为负数,而f(x)有明确的单调性,故必有一个常数a,使![]() 恒为正数,即
恒为正数,即![]()
∴![]()
∴![]() 上为增函数
上为增函数
∴a的取值范围为(0,3]
(II)假设f(x0)≠x0,则![]()
∵![]() 上为增函数,且
上为增函数,且![]()
∴当![]()
或当![]() 矛盾。
矛盾。
∴假设错误。
∴![]() 。
。