高三数学第二次模拟考试试卷

高三数学第二次模拟考试试卷

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分。考试时间120分钟。

第Ⅰ卷（选择题，共60分）

一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的

1、函数y=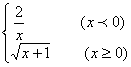的定义域是（　　  ）

A、{xx≠0}　　B、{xx∈R}　　　 C、{xx≥-1且x≠0}　　 D、{xx≥-1}

2、函数①y=2（x-1）²-1　②y=x²-3x+4　③y=　 ④y=中即非奇函数也非偶函数的是（　　　　）

A、①②③　　  B、①③④　　　 C、①③　　　D、①

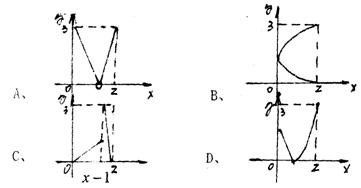
3、对于集合A={x0≤x≤2} B={y0≤y≤3}则同下列四个图形给出的对应f中，能构成从A到B的映射：f：A→B的是（　　  ）

4、已知函数y=（-1＜x＜1），则函数的值域是（　　  ）

A、{yy＜0}　　B、{y-1＜y＜0}　 C、{yy＞0}　　D、{yy≠1}

5、若复数z满足z-=，则z等于（　　 ）

A、-3+4i　　　 B、-3-4i　　　　  C、3-4i　　　　D、3+4i

6、下列极限中，其值等于2的是（　　　 ）

A、　　　　　  B、

C、　　 D、

7、函数y=1+3x-x³有（　　  ）

A、极小值-2，极大值2　　　 B、极小值-2，极大值3

C、极小值-1，极大值1　　　 D、极小值-1，极大值3

8、函数f（x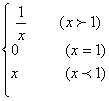）=在x=1处不连续是因为（　　　）

A、f（x）在x=1处无定义　　　B、f（x）不存在　

C、f（x）≠f（1）　　　　 D、f（x）≠f（x）

9、已知函数f（x）=lg（a^x-b^x）（a、b为常数，a＞1＞b＞0），若x∈（1，∞）时，f（x）＞0恒成立，则（　　 ）

A、a-b≥1　　　B、a-b≤1　　　　C、a-b＞1　　　 D、a=b+1

10、已知不等式mx²+px+1＞0的解集是{x2＜x＜3}，则M（p，q）的轨迹是（　　 ）

A、直线　　　 B、射线　　　　  C、直线的一部分 D、线段

11、对于每一个实数x，设f（x）取4x+1，x+2，-2x+4中的最小值，那么f（x）的最大值是（　　　）

A、　　　　 B、　　　　　  C、　　　　  D、

12、已知两个复数集合，M={ZZ=cosθ+（4-m²）i，m∈R，θ∈R}，

N={ZZ=m+（λ+sinθ）i，m∈R，θ∈R}，且M∩N≠φ，则实数λ的取值范围是（　　　）

A、{λ1≤λ≤5}　　B、{λ1≤λ≤3}　　C、{λλ≤5}　　D、{λλ≤3}

第Ⅱ卷（非选择题，共90分）

二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。

13、已知U={xx²＜50，x∈N₊}，C_UM∩L{1，6}，M∩C_UL={2，3}，C_U（M∪N）={5}则集合M=　　　　  集合L=　　　　 

14、厂家为回收空瓶，规定三个空瓶可换一瓶啤酒，有人订购10瓶啤酒，则此人能喝　　 瓶啤酒。

15、测量大气温度T时，发现在高空11千米以内，离地面距离越远，温度T越低，大约每升高一千米降温6℃，在11千米以外的上空，其温度几乎不变，如果地面温度是19℃，则T关于h的函数关系是　　　　　  。

16、已知函数f（x）存在反函数f^-1（x），且f（x）+ f（-x）=K（K为常数）则f^-1（x-K）+ f^-1（2K-x）=　　　　  。

二、解答题：本大题共6小是题，共74分。解答应写出文字说明，证明过程或演算步骤。（本小题12分）

17、已知函数f（x）=x³+（m-4）x²-3mx+（n-6）（x∈R）的图象关于原点对称（m，n∈R）

（1）求m，n的值

（2）证明f（x）在区间[-2，2]上为单调函数。

18、已知P：1-≤2，q：x²+2x+1-m²≤0（m＞0），若┌P是┑q的必要不充分条件，求实数m的取值范围。

19、已知x，y∈R，a为正常数，且函数f（x）满足f（x+a）=

求证：f（x）是周期函数

20、已知f（x）=x²-2tx+1，其定义域为{x0≤x≤1或7≤x≤8}

（1）f（x）在定义域内是否一定有反函数？

（2）当f（x）在定义域内有反函数时，求t的范围。

21、对于定义的区间D上的函数f（x），若实数x₀∈D，满足f（x₀）=x₀则称x₀为函数f（x）在D上的一个不动点。

（1）求函数f（x）=2x+-2 在（0，+∞）上的不动点。

（2）若函数f（x）=2x++a 在（0，+∞）上没有不动点，求a的取值范围

（3）设f（x）的不动点数目是有限多个，且f（x）定义域为R，下述命题是否正确？若正确请给予证明；若不正确，请举例说明

①若f（x）是奇函数，则f（x）的不动点数目是奇数。

②若f（x）是偶函数，则f（x）的不动点数目是偶数。

22、求函数y=2a-在x∈（0，1）]上的最大值（其中a∈R）

二模考试数学参考答案

一、选择题

1B  2C　3D　4A  5D　6D　7D  8C　9A　10C  11A　12C

二、填空题

13、M={2，3，4，7}L={1，6，4，7}　　　 14、15

　　　　-6h+19（0≤h≤11）

15、T　　　　　　　　　　　　　 16、0

　　　  -47　　（h＞11）

三、解答题：

17、解：（1）∵f（x）图象关于原点对称　 ∴f（x）是奇函数　 ∴f（-x）=- f（x）

解之m=4，n=6　　∴f（x）=x³-12x　　（6分）

（2）f′（x）=3x²-12=3（x²-4）当-2≤x≤2时，f′（x）＜0，∴f（x）在[-2，2]上是减函数，即单调函数（12分）

18、解：P：-2≤x≤10　　∴＞P：x＜-2或x＞10

q：-1-M≤x≤-1+m　　∴＞q：x＜-1-m或x＞-1+m

设A={xx＜-2或x＞10＝}　 B={xx＜-1-m或x＞-1+m＝}（5分）

∵＞P是＞q的必要不充分条件　　∴BA　　∴　m＞0

-1-m≤-2　　　或

-1+m＞10

m＞0

-1-m＜-2　 解之　m≥11（10分）

-1+m≥0

19、证明：∵f（x+a）=　　∴f（x+2a）==-（6分）

∴f（x+4a）=f[（x+2a）+2a]=-= f（x）

∴f（x）是以4a为周期的周期函数（12分）

20、解：（1）取t=有　f（0）=f（1）=1　　∴f（x）在定义域内不一定有反函数（4分）

（2）∵f（x）在x∈R时　其对称轴为x=t

当t≤0时，f（x）在其定义域内为增函数　　∴此时f（x）有反函数（6分）

同理为t≥8时，f（x）在其定义域内也有反函数（8分）

当1≤t≤4时，f（x）的图象在x∈[0,1]的一段此在x∈[7,8]的一段更靠近对称轴，那么要使f（x）有反函数，应有f（0）＜f（7）

则此时1≤t＜（10分）

当4≤t≤7时，同理有f（8）＜f（1），此时＜t≤7

由以上知，f（x）在其定义域内有反函数的范围为：t≤0或

1≤t＜或＜t≤7或t≥8 （12分）

21、解：（1）设x₀是f（x）在（0，+∞）上的不动点，则f（x₀）=x₀　 即2x₀+-2=x₀

解得x₀=1（2分）

（2）∵f（x）在（0，+∞）上没有不动点，亦即2x++a=x在x∈（0，+∞）上无解。

即x+=-a在x∈（0，+∞）上无解　　又∵当x∈（0，+∞）时，

x+≥2　　 ∴只要-a＜2　　即a＞-2（4分）

（3）①正确　 ∵f（x）为奇函数　 且x∈R　　∴f（0）=0　　∴0是f（x）的一个动点，假设　x₀≠0是f（x）的一个不动点，则有f（x₀）=x₀

又f（x₀）=-f（-x₀）　 ∴f（-x₀）=-x₀　  ∴-x₀也是一个不动点

显然x₀≠-x₀这表明f（x）的解。不动点如果存在，则必成对，又根据题设f（x）只有有限个不动点，因此f（x）的不动点数目为奇数（6分）

（4）不正确　 例如函数f（x）=1　 若x₀为不动点　则f（x₀）=x₀

又∵f（x₀）=1　　∴x=1　　∴f（x）=1只有一个不动点（2分）

22、（14分）解：设=t，则有y=2at-（t∈[0，1]），即求该函数的最大值，

当a≥0时，易让f（t）=2at-（t∈（0，1））为幸函数（2分）

∴a≥0时　 f_max（t）=f(1)=2a-1（2分）

以下先考虑a＜0时，f（t）在t＞0上的单调性

∵f′（t）=2a+　 令f′（t）=0，当t=-　　当t∈（0，-）时，f′（t）＞0

当t∈（- ，+∞）时f′（t）＜0， ∴f（t）在t∈（0，- ）为增函数，

在t[-，+∞）为减函数（8分）

∵当-1≤a＜0时，-≥1　　∴f（t）在t∈（0，1]上为增函数

∴此时f（t）_max= f（1）=2a-1　 当a＜-1时　- ＜1

则f（t）在t∈（0，）上为增函数　 在t∈[-，1]上为减函数

∴f（t）_max=f（- ）=-3（12分）

综上　a≥-1时　f(t)_max=2a-1（t=1取到）a＜-1f(t)_max=-3·（t-取到）